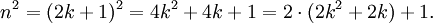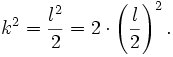- Mathematische Beweismethode
-
Ein Beweis ist in der Mathematik die als fehlerfrei anerkannte Herleitung der Richtigkeit oder auch Unrichtigkeit einer Aussage aus einer Menge von Axiomen, die als wahr vorausgesetzt werden, und anderen Aussagen, die bereits bewiesen sind.
Man kann nach zwei Kriterien Beweise unterscheiden und in zwei Gruppen aufteilen:
- Ein Beweis kann entweder direkt oder indirekt geführt werden.
- Ein Beweis kann entweder konstruktiv oder nicht-konstruktiv sein.
Umfangreichere Beweise werden in der Regel in mehrere kleine Teilbeweise aufgeteilt, von denen dann einige direkt und andere indirekt, einige konstruktiv und andere nicht-konstruktiv sein können.
Inhaltsverzeichnis
Direkte und indirekte Beweise
Bei einem direkten Beweis wird die Behauptung durch Anwendung von bereits bewiesenen Aussagen und durch logische Folgerungen bewiesen.
Dazu ein Beispiel:
Behauptung 1: Das Quadrat einer ungeraden natürlichen Zahl n ist ungerade.
Beweis: Es sei n eine ungerade natürliche Zahl. Dann lässt sich n darstellen als n = 2k + 1, wobei k eine natürliche Zahl oder Null ist. Daraus folgt mit Hilfe der ersten binomischen Formel
Aus dieser Darstellung folgt, dass n2 ungerade ist.
Bei einem indirekten Beweis (Widerspruchsbeweis) zeigt man, dass ein Widerspruch entstünde, wenn die zu beweisende Behauptung falsch wäre. Dazu nimmt man an, dass die Behauptung falsch ist und wendet die gleichen Methoden wie beim direkten Beweis an. Wenn daraus ein Widerspruch entsteht, dann kann die Behauptung nicht falsch sein, also muss sie richtig sein (Satz vom ausgeschlossenen Dritten). Wichtige (und keinesfalls selbstverständliche!) Voraussetzung für die Gültigkeit eines Widerspruchbeweises ist, dass im zugrunde liegenden System die Aussage nicht gleichzeitig wahr und falsch sein kann (Widerspruchsfreiheit).
Ein klassisches Beispiel eines Widerspruchsbeweises ist der Nachweis, dass es unendlich viele Primzahlen gibt.
Hier noch zwei weitere Beispiele:
Behauptung 2: Ist die Wurzel aus einer geraden natürlichen Zahl n eine natürliche Zahl, so ist diese gerade.
Beweis: Es wird angenommen, dass
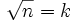 ungerade sei. Dann ist wegen der bereits bewiesenen Behauptung 1 auch k2 = n ungerade und das ist ein Widerspruch zu der Voraussetzung, dass n gerade ist. Also ist die getroffene Annahme falsch, das heißt,
ungerade sei. Dann ist wegen der bereits bewiesenen Behauptung 1 auch k2 = n ungerade und das ist ein Widerspruch zu der Voraussetzung, dass n gerade ist. Also ist die getroffene Annahme falsch, das heißt, 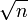 ist gerade.
ist gerade.Behauptung 3: Die Zahl
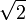 ist irrational.
ist irrational.Beweis: Wir nehmen an, diese Zahl sei rational. Dann kann man sie als Bruch
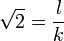 darstellen, wobei l und k natürliche Zahlen und ohne Beschränkung der Allgemeinheit teilerfremd sind (sonst kann man den Bruch soweit kürzen, bis das der Fall ist). Daraus folgt durch Quadrieren
darstellen, wobei l und k natürliche Zahlen und ohne Beschränkung der Allgemeinheit teilerfremd sind (sonst kann man den Bruch soweit kürzen, bis das der Fall ist). Daraus folgt durch Quadrieren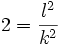 , also
, also 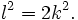
Folglich ist l2 eine gerade Zahl. Da die Wurzel aus einer geraden Quadratzahl auch gerade ist (Behauptung 2) ist l selbst gerade, also ist l/2 eine natürliche Zahl. Durch Umformung der letzten Gleichung erhält man
Das zeigt, dass k2 und somit auch k gerade natürliche Zahlen sind. Also sind l und k gerade und haben somit beide den Teiler 2. Damit sind l und k nicht teilerfremd – im Widerspruch zu der Annahme der Teilerfremdheit von l und k. Also ist auch die ursprüngliche Annahme,
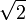 sei rational, falsch.
sei rational, falsch.Dieser Beweis ist insgesamt ein indirekter Beweis, obwohl einige Teilaussagen direkt hergeleitet werden.
Konstruktive und nicht-konstruktive Beweise
Bei einem konstruktiven Beweis wird entweder die Lösung selbst genannt oder ein Verfahren angegeben, das zur Lösung führt, das heißt, es wird eine Lösung konstruiert.
Bei einem nicht-konstruktiven Beweis wird anhand von Eigenschaften auf die Existenz einer Lösung geschlossen. Manchmal wird sogar indirekt die Annahme, es gäbe keine Lösung, zum Widerspruch geführt, woraus folgt, dass es eine Lösung gibt. Aus solchen Beweisen geht nicht hervor, wie man die Lösung gewinnt.
Ein einfaches Beispiel soll dies verdeutlichen.
Behauptung: Die Funktion f(x) = 2x - 1 besitzt im Intervall [0,1] eine Nullstelle x0.
Konstruktiver Beweis: Sei x0 = 0,5. Dann gilt f(x0) = 2·x0 - 1 = 2·0,5 - 1 = 1 - 1 = 0. Ferner liegt x0 = 0,5 im Intervall [0,1]. Damit ist die Behauptung bewiesen. Die Nullstelle ist sogar mit x0 = 0,5 angegeben.
Nicht-konstruktiver Beweis: f ist stetig. Ferner ist f(0) = -1 < 0 und f(1) = 1 > 0. Nach dem Zwischenwertsatz für stetige Funktionen folgt die Behauptung. Über den Wert der Nullstelle ist jedoch nichts bekannt.
Einige besondere Beweismethoden
In der Geschichte der Mathematik wurden zum Beweis bestimmter Aussagen Beweismethoden entwickelt, die sich auch als nützlich für den Beweis anderer Aussagen erwiesen haben und dadurch zu Standard-Beweismethoden wurden.
Hier eine Auswahl:
Vollständige Induktion
Der Beweis durch vollständige Induktion ist ein oft angewendetes Verfahren zum Beweis von Sätzen der Form „Für jede natürliche Zahl n gilt ...“. Dazu zeigt man zuerst, dass die Aussage für n=0 (oder auch einen anderen Anfangswert n0) gilt, und danach, dass sie auch für n+1 gilt, wenn sie für n gilt. Die vollständige Induktion lässt sich mit einem Domino-Effekt vergleichen. Man stellt die Steine so auf, dass, wenn einer umfällt, auch der nächste umfällt (n -> n+1), und stößt den ersten Stein um (n=0).
Ein einfaches Beispiel:
Behauptung: 1 + 3 + ... + (2n+1) = (n+1)²
Beweis:
- Die Aussage gilt für n = 0: (2*0+1) = 1 = (0+1)² ist eine wahre Aussage.
- Die Behauptung sei für ein beliebiges n gültig. Für n+1 untersucht man die Summe
- 1 + 3 + ... + (2n+1) + (2n+3)
- Da die Behauptung für n gültig ist, folgt
- 1 + 3 + ... + (2n+1) + (2n+3) = (n+1)² + (2n+3) = (n+1)² + 2(n+1) + 1 = ((n+1) + 1)²
Also gilt die Behauptung auch für n+1, damit ist die Aussage nach dem Induktionsprinzip bewiesen.
Vollständige Fallunterscheidung
Beim Beweis einer Aussage durch vollständige Fallunterscheidung wird eine endliche Anzahl von Fällen betrachtet, die in ihrer Gesamtheit alle möglichen Fälle überdecken und von denen jeder eine einfachere Behandlung des Problems ermöglicht.
Behauptung: Jede Primzahl
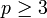 hat die Form
hat die Form 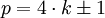 für eine natürliche Zahl k.
für eine natürliche Zahl k.Beweis: Man unterscheidet folgende vier Fälle für die Zahl p, von denen immer genau einer eintritt:
- p = 4k
- p = 4k + 1
- p = 4k + 2
- p = 4k + 3 = 4(k + 1) − 1
Im ersten dieser Fälle ist p durch 4 teilbar und damit keine Primzahl, im dritten Fall ist p durch 2 teilbar und somit ebenfalls keine Primzahl. Also muss einer der Fälle zwei oder vier eintreten, das heißt p hat die Form
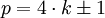 für eine natürliche Zahl k.
für eine natürliche Zahl k.Es sei angemerkt, dass die Fallunterscheidung zwar vollständig sein muss, aber die untersuchten Fälle sich nicht gegenseitig ausschließen müssen.
Diagonalverfahren
Die Diagonalverfahren wurden von Georg Cantor zum Beweis von zwei speziellen Aussagen entwickelt, sie haben sich seitdem als allgemeine Beweismethoden bewährt.
Das erste Cantorsche Diagonalverfahren ist ein direkter Beweis für die Abzählbarkeit einer Menge. Es wird gezeigt, dass man jedem Element der zu untersuchenden Menge eine natürliche Zahl zuordnen kann.
Das zweite Cantorsche Diagonalverfahren ist ein indirekter Beweis für die Überabzählbarkeit einer Menge. Es wird also das Gegenteil angenommen, nämlich dass die Menge abzählbar sei. Dann wird aus dieser Annahme ein Widerspruch hergeleitet, sodass sie fallen gelassen werden muss.
Schubfachprinzip
Das Schubfachprinzip geht auf den deutschen Mathematiker Dirichlet zurück und kann sehr anschaulich formuliert werden: Verteilt man n+1 Gegenstände auf n Schubfächer, dann befinden sich in mindestens einem Schubfach mindestens zwei Gegenstände.
Transfinite Induktion
Bei der transfiniten Induktion wird die vollständige Induktion auf beliebige wohlgeordnete Mengen verallgemeinert.
Siehe auch
Literatur
- Martin Aigner, Günter M. Ziegler: Das Buch der Beweise. Springer, Berlin 2004, ISBN 3-540-40185-7
Weblinks
Wikimedia Foundation.