- Approximationssatz von Runge
-
In der Funktionentheorie beschäftigt sich die Runge-Theorie mit der Frage, wann auf einem Teilgebiet holomorphe Funktionen durch auf einem größeren Gebiet holomorphe Funktionen approximiert werden können. Sie wurde wesentlich von Carl Runge entwickelt, der 1885 seinen Approximationssatz veröffentlichte.
Inhaltsverzeichnis
Runge-Theorie für Kompakta
Für eine Menge
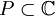 sei
sei ![\mathbb{C}_P[z]](/pictures/dewiki/100/db180d889a389640516692c4bf806b46.png) die
die 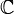 -Algebra der rationalen Funktionen, die nur in P Polstellen aufweisen.
-Algebra der rationalen Funktionen, die nur in P Polstellen aufweisen.Der Runge'sche Approximationssatz für Kompakta besagt nun: Sei
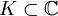 ein Kompaktum. Trifft
ein Kompaktum. Trifft 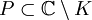 jede beschränkte Komponente von
jede beschränkte Komponente von 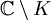 , dann ist jede auf K holomorphe Funktion gleichmäßig durch Funktionen aus
, dann ist jede auf K holomorphe Funktion gleichmäßig durch Funktionen aus ![\mathbb{C}_P[z]](/pictures/dewiki/100/db180d889a389640516692c4bf806b46.png) approximierbar.
approximierbar.Als wichtigen Spezialfall erhält man den Kleinen Satz von Runge: Wenn für ein Kompaktum
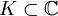 das Komplement einfach zusammenhängend ist, dann ist jede auf K holomorphe Funktion gleichmäßig durch Polynome approximierbar.
das Komplement einfach zusammenhängend ist, dann ist jede auf K holomorphe Funktion gleichmäßig durch Polynome approximierbar.Runge-Theorie für Bereiche
Der Satz von Runge über rationale Approximation lautet: Sei
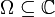 ein Bereich und
ein Bereich und 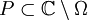 eine Menge, deren Abschluss
eine Menge, deren Abschluss 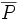 in
in 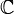 jedes Loch von Ω trifft. Dann liegt die Algebra
jedes Loch von Ω trifft. Dann liegt die Algebra ![\mathbb{C}_P[z]](/pictures/dewiki/100/db180d889a389640516692c4bf806b46.png) dicht in der Algebra der holomorphen Funktionen
dicht in der Algebra der holomorphen Funktionen 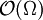 . Als Loch wird hierbei eine kompakte Komponente von
. Als Loch wird hierbei eine kompakte Komponente von 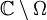 bezeichnet.
bezeichnet.Zwei Bereiche
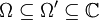 heißen Runge'sches Paar, wenn jede auf Ω holomorphe Funktion sich auf Kompakta gleichmäßig durch auf Ω' holomorphe Funktionen approximieren lässt. Aus obigem Approximationssatz folgt mit Hilfe des Satzes von Behnke-Stein schließlich die Charakterisierung:
heißen Runge'sches Paar, wenn jede auf Ω holomorphe Funktion sich auf Kompakta gleichmäßig durch auf Ω' holomorphe Funktionen approximieren lässt. Aus obigem Approximationssatz folgt mit Hilfe des Satzes von Behnke-Stein schließlich die Charakterisierung: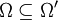 bilden genau dann ein Runge'sches Paar, wenn
bilden genau dann ein Runge'sches Paar, wenn 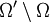 keine kompakten Komponenten hat, also Ω relativ zu Ω' keine Löcher aufweist.
keine kompakten Komponenten hat, also Ω relativ zu Ω' keine Löcher aufweist.
Anwendungen
- Der Satz von Mittag-Leffler lässt sich aus den Runge'schen Sätzen herleiten.
- Es existieren punktweise konvergente Polynomfolgen, die nicht auf allen Kompakta lokal gleichmäßig konvergieren.
- Die Einheitskreisscheibe lässt sich holomorph und eigentlich in
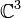 einbetten. (Tatsächlich sogar in
einbetten. (Tatsächlich sogar in 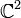 , was aber nicht direkt aus den Runge'schen Sätzen folgt.)
, was aber nicht direkt aus den Runge'schen Sätzen folgt.) - Jedes Gebiet von
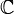 ist ein Holomorphiegebiet, d. h. zu jedem Gebiet gibt es eine darauf definierte holomorphe Funktion, die sich nicht holomorph über dieses Gebiet hinaus ausdehnen lässt.
ist ein Holomorphiegebiet, d. h. zu jedem Gebiet gibt es eine darauf definierte holomorphe Funktion, die sich nicht holomorph über dieses Gebiet hinaus ausdehnen lässt.
Verallgemeinerungen
- auf Riemannsche Flächen, durch Behnke und Stein 1948[1]
- Satz von Mergelyan, durch Mergelyan 1951[2]; behandelt zusätzlich u. a. das Problem mit stetiger Fortsetzung auf den Rand
Literatur
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 2. Springer, Berlin 2007, ISBN 978-3-540-57052-3
Wikimedia Foundation.
