- Marilyn vos Savant
-
Marilyn vos Savant [mæɹɪlɪn vɑs sə'vɑnt] (* 11. August 1946 in St. Louis, Missouri; gebürtig Marilyn Mach) ist eine US-amerikanische Kolumnistin und Autorin. Sie schreibt die Kolumne „Ask Marilyn“, die in der Sonntagszeitung „Parade“ veröffentlicht wird, und hat mehrere Ratgeber und Bücher verfasst, in denen sie sich hauptsächlich mit mathematischen Problemen und gesellschaftlichen Fragen auseinandersetzt. In einigen ihrer Ratgeber befasst sich vos Savant außerdem mit Methoden, die zu einer Verbesserung des Intellekts beitragen sollen. Aufgrund mehrerer weit überdurchschnittlicher Ergebnisse, die sie bei verschiedenen Intelligenztests erzielte, wurde vos Savant in den von 1986 bis 1989 erschienenen Editionen des Guinness-Buches der Rekorde unter der Rubrik „höchster Intelligenzquotient“ aufgeführt. Deswegen wird vos Savant von den Medien mitunter als die „intelligenteste Person der Welt“[1] oder als „klügste Frau weltweit“[2] bezeichnet.
Das größte öffentliche Aufsehen erregte sie jedoch, als sie 1990 in ihrer Kolumne „Ask Marilyn“ ihre Lösung zu dem so genannten „Ziegenproblem“ publizierte. Obwohl ein großer Teil der Personen, die mit vos Savants Aussage konfrontiert wurden, ihre Lösung zu dieser Aufgabe aus der Wahrscheinlichkeitstheorie für unwahr hielt, konnte letzten Endes bewiesen werden, dass der von ihr erläuterte Lösungsweg zu einem mathematisch korrekten Ergebnis führt.
Inhaltsverzeichnis
Biographie
Herkunft und Familie
Marilyn vos Savant wurde am 11. August 1946[3] in St. Louis im US-Bundesstaat Missouri[4] geboren. Ihr Geburtsname lautet Marilyn Mach,[5] doch entgegen der Tradition nahm sie später als Familiennamen den Geburtsnamen ihrer Mutter an. Sie vertritt die Ansicht, dass Jungen grundsätzlich den Nachnamen ihres Vaters und Mädchen den Familiennamen ihrer Mutter tragen sollten.[6] Vos Savant war das jüngste Kind von Joseph Mach, einem aus einer Bergarbeiterfamilie stammenden deutschen Einwanderer,[7] und Marina vos Savant, einer italienischen Immigrantin.[8][9] Das Ehepaar betrieb ein Restaurant in einem Arbeiterviertel von St. Louis und eröffnete später eine Kette von Reinigungen.[10] Neben Marilyn vos Savant hatten Joseph Mach und Marina vos Savant noch zwei ältere Söhne namens Robert und Joseph junior.[8] Den Nachnamen „Savant“ trugen mehrere Mitglieder von vos Savants Familie: Tatsächlich hießen ihre Großeltern mütterlicherseits Giuseppe vos Savant und Maria Savant.[11] Es war allerdings Zufall, dass deren Familiennamen vor der Eheschließung beinahe identisch lauteten.[12] Darüber hinaus zählt Marilyn vos Savant unter ihren Vorfahren den österreichischen Physiker und Philosophen Ernst Mach (1838-1916).[13]
In ihrer Kolumne hat Marilyn vos Savant behauptet, dass sie als Heranwachsende niemals über die Bedeutung des Wortes „Savant“, das so viel wie „Wissender“ oder „Gelehrter“ bedeutet, nachgedacht habe.[11]
Kindheit und Jugend
Im Laufe ihrer Schulzeit wurde vos Savant mehrere Male einem Intelligenztest unterzogen, wobei sie bei jeder dieser Prüfungen exzellente Ergebnisse erreichte. Während ihr Umfeld auf diese Resultate mit großem Erstaunen reagierte, verspürte vos Savant keinerlei Verblüffung angesichts ihrer Testergebnisse, sondern empfand diese als völlig normal, wie sie 2009 in einem Interview mit der „Financial Times“ angab. Der lokale Schuldirektor befreite vos Savant teilweise vom Unterricht und teilte ihr verschiedene Aufgaben zu, so dass ihr, während sie die ihr zugewiesene Arbeit in seinem Büro ausführte, ein Einblick in die Intelligenztestresultate ihrer Mitschüler gewährt wurde. Ihre Beschäftigung bestand größtenteils darin, im Voraus deren Ergebnisse zu erraten, wobei ihre Vermutungen auf Gesprächen fußten, die sie mit ihnen zuvor geführt hatte.[8]
In einem Interview, das sie 2009 der kolumbianischen Zeitschrift „Semana“ gewährte, enthüllte Marilyn vos Savant, keine einfache Kindheit gehabt und den Schulbesuch verabscheut zu haben. Als Mädchen sei sie aufgrund ihres Geschlechtes stets mit Geringschätzung behandelt worden. Ihre Lehrer hätten ihre Intelligenz als eine „nutzlose Eigenschaft“ betrachtet. Einmal sei sie von ihrem Lehrer aus dem Unterricht verwiesen worden, da sie in seinem Kursus in weiterführenden Naturwissenschaften die einzige weibliche Schülerin war.[9] In der Schule habe sie sich gelangweilt, allerdings nicht, weil der Schulstoff ihr zu leicht gefallen wäre, sondern weil der Unterricht „überaus monoton“ gewesen sei.[14] Als vos Savant ihren Schulabschluss machte, befand sie sich in einem Jahrgang von 613 Schülern auf dem 178. Platz. Zunächst besuchte sie das Meramec Community College, bevor sie an der Washington University in St. Louis ein Studium der Philosophie aufnahm. Nach zwei Jahren brach sie das Studium auf Drängen ihrer Eltern jedoch ab; jene rieten ihr, ein „nützlicheres“ Fach als Studiengang zu belegen.[7] Vos Savant befasste sich daraufhin mit Aktien, Investment und Immobilien[15] und arbeitete für die Reinigungskette ihrer Eltern.[8] Ihren seit ihrer Kindheit gehegten Wunsch, Schriftstellerin zu werden,[16] konnte sie erst verwirklichen, nachdem sie durch ihre Tätigkeiten im Immobilienbereich finanzielle Unabhängigkeit erlangt hatte. Vos Savant verfasste Kurzgeschichten, Essays und Zeitungsartikel. Den Umstand, dass diese stets unter einem Pseudonym veröffentlicht wurden, begründete sie damit, dass sie ihren Namen nicht für die Veröffentlichung von Werken missbrauchen wollte, die ihrer Meinung nach zu große Mängel aufwiesen.[17]
Privatleben
Genau wie ihre Mutter und Großmutter mütterlicherseits ging vos Savant ihre erste Ehe im Alter von sechzehn Jahren ein.[7] Von ihrem ersten Ehemann wurde sie jedoch nach zehn Jahren geschieden.[5] Aus dieser Verbindung stammen ihre beiden Kinder Mary und Dennis Younglove.[18] Vos Savants zweite Ehe, die ebenfalls zehn Jahre dauerte,[5] blieb hingegen kinderlos und endete in einer Scheidung, als sie 35 Jahre alt war. Zu diesem Zeitpunkt begann sie, über einen Wegzug aus ihrer Geburtsstadt nachzudenken; sie konnte sich dazu jedoch erst nach dem Tod ihres Vaters im Jahre 1986[19] entschließen.[8]
Am 23. August 1987 vermählte sich die 41-jährige Marilyn vos Savant mit dem Wissenschaftler und Unternehmer Robert Jarvik. Für vos Savant ist es die dritte, für Jarvik die zweite Ehe.[20] Seine Heirat mit Marilyn vos Savant wurde von dem Schriftsteller Isaac Asimov als ein „true meeting of the minds“ bezeichnet,[21] ein Beiname, der sich auf vos Savants Intelligenzquotienten sowie auf die Tatsache bezieht, dass Jarvik als der Erfinder des künstlichen Herzens gilt.[22] Das von ihm kreierte Jarvik-7 konnte im Jahre 1982 als erstes brauchbares Herzimplantat eingesetzt werden. Seiner Ehe mit Marilyn vos Savant sind jedoch keine Kinder entsprungen.[23] Seit den 1980er Jahren wohnt Marilyn vos Savant mit ihrer Familie im New Yorker Stadtteil Manhattan. Ihre Tochter Mary hat mit ihrem Ehemann David zwei Töchter namens Valerie und Michelle.[4]
Berufliche Tätigkeiten
Marilyn vos Savant ist Leiterin des Finanzwesens beziehungsweise Chief Financial Officer des Jarvik-Unternehmens,[24] übt allerdings auch eine wissenschaftliche Tätigkeit aus, wobei sie sich hauptsächlich auf Recherchen über die Herz-Kreislauferkrankungen konzentriert.[25] Sie hält außerdem Vorlesungen an Universitäten und Firmen.[12] Ihre Kinder Mary und Dennis, die beide Medizin studiert haben,[26] arbeiten heute ebenfalls für das Jarvik-Unternehmen.
Vos Savant ist Mitglied des Committee for the Scientific Investigation of Claims of the Paranormal und hat im Vorstand des „National Council of Economic Education“[27] und der „National Association for Gifted Children“ gearbeitet.[14] Ferner ist sie Mitglied der Hochbegabtenclubs Mensa International[9] und Prometheus Society sowie der International Society for Philosophical Enquiry.[21] Mensa International trat sie 1969 bei, weil sie sich davon Unterstützung bei der Erziehung ihrer Kinder versprach.[8] Mitte der 1980er Jahre war Marilyn vos Savant außerdem Mitglied und Sekretärin der Mega Society, ein Hochbegabtenclub, dessen Mitglieder einen Intelligenzquotienten mit einem Prozentrang von mindestens 99,9999 % erzielt haben müssen.[28][29]
Hauptberuflich ist vos Savant, wie sie in Interviews angibt, allerdings Kolumnistin. Sie schreibt die Kolumne „Ask Marilyn“ (Frag Marilyn), die seit 1986 wöchentlich in der US-amerikanischen Sonntagszeitung „Parade“ erscheint. „Parade“ wird von ungefähr 72,8 Millionen Menschen gelesen, und von jeder Ausgabe entstehen 33 Millionen Exemplare.[30] In ihrer Kolumne nimmt vos Savant Fragen von Lesern entgegen, die ihr – zumeist mathematische oder sprachliche – Denksportaufgaben stellen, sie manchmal allerdings auch um eine Erklärung bestimmter kultureller Muster, um Rat im Allgemeinen oder um eine Antwort auf philosophische, technische oder naturwissenschaftliche Fragen bitten. Von Zeit zu Zeit publiziert vos Savant selbst eine Denksportaufgabe oder führt unter ihren Lesern eine Umfrage durch. Darüber hinaus veröffentlicht sie in ihrer Kolumne „Marilyn’s Weekly Quiz“, in dem sie meistens historische oder naturwissenschaftliche Fragen stellt,[31] sowie das von ihr erfundene Zahlenpuzzle „Numbrix“. Letzteres wird in Parade seit 2008 publiziert.[32]
„Ask Marilyn“ entstand, nachdem vos Savant 1986 das erste Mal im Guinness-Buch der Rekorde aufgeführt worden war. „Parade“ veröffentlichte daraufhin einen Artikel über vos Savant und publizierte im Nachhinein einige Fragen, die die Leser des Magazins ihr gestellt hatten sowie die Antworten, die sie darauf gegeben hatte.[25] Da „Parade“ fortlaufend Fragen zugesendet bekam, wurde „Ask Marilyn“ in eine Kolumne umgewandelt. Heute erhält Marilyn vos Savant von ihren Lesern täglich ungefähr dreihundert E-Mails.[9]
Marilyn vos Savants Kolumne wird sowohl gedruckt als auch im Internet veröffentlicht. Die virtuelle Version von „Ask Marilyn“ ergänzt insofern die gedruckten Ausgaben, als dort kontrovers diskutierte Antworten besprochen, Fehler korrigiert, Antworten erweitert, manche Fragen noch einmal gestellt und zusätzliche Fragen beantwortet werden.
Auf die Frage eines TV-Producers, weshalb sie weder für ein Wissenschaftsmagazin noch für eine Literaturzeitschrift eine Kolumne veröffentlichen würde, antwortete vos Savant: „Die intelligenten Einwohner dieses Landes lesen nicht derartige Magazine, sondern ‚Parade‘. Und das kann ich beweisen – dieser Umstand spiegelt sich nämlich in meiner Post wider.“[33]
Drei von Marilyn vos Savants Büchern, nämlich „Ask Marilyn: Answers to America’s Most Frequently Asked Questions“ (1992), „More Marilyn: Some Like It Bright!“ (1994), und „Of Course I’m for Monogamy: I’m Also for Everlasting Peace and an End to Taxes“ (1996), sind aus ihrer Kolumne entstanden. Alle drei Bücher beinhalten jeweils eine Sammlung von Fragen, Antworten und Rätseln, die in „Ask Marilyn“ veröffentlicht worden sind.
„Ziegenproblem“
Das „Ziegenproblem“, das im anglo-amerikanischen Sprachraum auch „Monty Hall Problem“ genannt wird, ist eine mathematische Aufgabe aus der Wahrscheinlichkeitstheorie. Es geht auf die Spielshow „Let’s Make a Deal“ zurück, die von dem kanadischen Showmaster Monty Hall moderiert wurde und vor allem in den 1960er und 1970er Jahren populär war.[34] Durch Marilyn vos Savants vorgeschlagene Lösung für das „Ziegenproblem“ erregte ihre Kolumne das größte öffentliche Aufsehen und löste eine breite Diskussion über dieses mathematische Problem aus. Am 9. September 1990 veröffentlichte vos Savant in ihrer Kolumne ihre Antwort auf die folgende Leserfrage:
„Suppose you’re on a game show, and you’re given the choice of three doors. Behind one door is a car, the others, goats. You pick a door, say #1, and the host, who knows what’s behind the doors, opens another door, say #3, which has a goat. He says to you: ‘Do you want to pick door #2?’ Is it to your advantage to switch your choice of doors?“
„Stellen Sie sich vor, Sie wären in einer Gameshow und müssten sich für eine von drei Türen entscheiden. Hinter einer Tür befindet sich der Gewinn, ein Auto, hinter den beiden anderen sind Ziegen versteckt. Sie entscheiden sich für Tür Nummer eins, und der Showmaster, welcher weiß, was sich hinter den jeweiligen Türen befindet, öffnet Tür Nummer drei, die eine Ziege bisher verborgen hatte. Nun stellt er Ihnen die Frage, ob Sie bei Nummer eins bleiben oder zu Tür Nummer zwei wechseln wollen. Sollte man bei seiner ursprünglichen Wahl bleiben oder wechseln?“
„Yes; you should switch. The first door has a 1/3 chance of winning, but the second door has a 2/3 chance. Here’s a good way to visualize what happened. Suppose there are a million doors, and you pick door #1. Then the host, who knows what’s behind the doors and will always avoid the one with the prize, opens them all except door #777,777. You’d switch to that door pretty fast, wouldn’t you?“
„Ja, man sollte besser wechseln. Bei Tür Nummer eins hat man eine Gewinnchance von 1/3, bei Tür Nummer zwei dagegen eine von 2/3. Das kann man sich folgendermaßen gut erklären: Stellen Sie sich vor, es stünden Ihnen eine Million Türen zur Verfügung; davon wählen Sie Tür Nummer eins. Daraufhin öffnet der Showmaster, welcher weiß, was die jeweiligen Türen verbergen und stets darauf achten wird, niemals die Tür mit dem Gewinn zu öffnen, alle anderen Türen mit Ausnahme der Tür Nummer 777 777. In so einem Fall würden Sie sich ziemlich schnell zu einem Wechsel entscheiden, oder?“
– Marilyn vos Savant: in ihrer Kolumne „Ask Marilyn“[35]
Marilyn vos Savants Antwort, man solle zu Tür Nummer zwei überwechseln, da man dadurch die Gewinnchance von 1/3 auf 2/3 verdoppeln würde, fand breite öffentliche Resonanz. Sie erhielt ungefähr zehntausend Briefe, von denen mehrere hundert von Professoren und anderen Akademikern stammten. 65 % der Promovierten, die an vos Savant schrieben, wollten sie davon überzeugen, dass sie im Unrecht sei; von den restlichen Absendern waren 92 % derselben Ansicht. Nach Meinung jener Absender bliebe die Wahrscheinlichkeit, einen Gewinn zu erlangen, für beide Türen gleich, also 1/2. Auf dieser Lösung beharrten unter anderem der stellvertretende Direktor des „Center for Defense Information“, ein Statistiker der „National Institutes of Health“[35] und der ungarische Mathematiker Paul Erdős. Letzterer ließ sich erst dann von vos Savants Lösung überzeugen, nachdem man durch Computersimulation einhundert Runden des Experimentes durchgespielt und dabei ein Wechsel der Tür häufiger zum Erlangen des Gewinnes geführt hatte.[34]
Ferner wurde das „Ziegenproblem“ von Mitarbeitern der Central Intelligence Agency, von Mathematikern des Massachusetts Institute of Technology, von Programmierern des Los Alamos National Laboratory in New Mexico und in mehr als tausend amerikanischen Schulen analysiert.[36] Ab Juli 1991 wurde auch in der deutschen Öffentlichkeit über das „Ziegenproblem“ diskutiert, als Die Zeit über dieses mathematische Problem und die von vos Savant erläuterte Lösung berichtete. Die Reaktion auf vos Savants Gedankengang fiel ähnlich negativ aus wie in den Vereinigten Staaten.[37]
Trotz der weitgehend negativen Reaktion auf ihre Antwort weigerte sich Marilyn vos Savant, ihre Aussage zu widerrufen. In ihrer zweiten Kolumne zum Thema „Ziegenproblem“, die sie am 2. Dezember 1990 veröffentlichte,[38] argumentierte sie folgendermaßen:
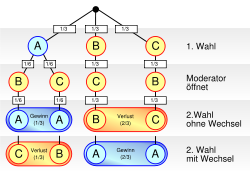
„My original answer is correct. But first, let me explain why your answer is wrong. The winning odds of 1/3 on the first choice can’t go up to 1/2 just because the host opens a losing door. To illustrate this, let’s say we play a shell game. You look away, and I put a pea under one of three shells. Then I ask you to put your finger on a shell. The odds that your choice contains a pea are 1/3, agreed? Then I simply lift up an empty shell from the remaining other two. As I can (and will) do this regardless of what you’ve chosen, we’ve learned nothing to allow us to revise the odds on the shell under your finger. The benefits of switching are readily proven by playing through the six games that exhaust all the possibilities. For the first three games, you choose #1 and “switch” each time, for the second three games, you choose #1 and “stay” each time, and the host always opens a loser. Here are the results:“
„Meine ursprüngliche Antwort ist korrekt. Zuerst lassen Sie mich jedoch erklären, weshalb Ihre Antwort falsch ist. Die Wahrscheinlichkeit, dass man mit der ersten Türwahl gewinnt, kann nicht von 1/3 auf 1/2 steigen, lediglich weil der Showmaster eine Tür mit einer Ziege öffnet. Um dies zu veranschaulichen, schlage ich vor, dass wir ein Schalenspiel spielen. Sie sehen weg, und ich lege eine Erbse unter eine von drei vorhandenen Schalen. Dann bitte ich Sie, Ihren Finger auf eine Schale zu legen. Die Wahrscheinlichkeit, dass unter der von Ihnen ausgewählten Schale eine Erbse liegt, beträgt 1/3, einverstanden? Dann entferne ich einfach eine der beiden übrig gebliebenen Schalen, von der ich weiß, dass sie leer ist. Da ich dies unabhängig von Ihrer Wahl tun kann (und werde), haben wir nichts erfahren, was uns zu der Annahme leiten könnte, dass sich die Gewinnchancen geändert hätten. Die Vorteile, die man aus einem Wechsel ziehen kann, werden deutlich, indem man alle möglichen sechs Abläufe des Spiels durchspielt. Während der ersten drei Runden wählen Sie Tür Nummer eins und wechseln jedes Mal; während der nächsten drei Runden wählen Sie wieder Tür Nummer eins, wechseln aber nicht, und der Showmaster öffnet jedes Mal eine Tür ohne Gewinn. Hier sind die Ergebnisse:[35]“
-
-
Tür 1 Tür 2 Tür 3 Ergebnis Spiel 1 Auto Ziege Ziege Man wechselt und verliert. Spiel 2 Ziege Auto Ziege Man wechselt und gewinnt. Spiel 3 Ziege Ziege Auto Man wechselt und gewinnt. Spiel 4 Auto Ziege Ziege Man wechselt nicht und gewinnt. Spiel 5 Ziege Auto Ziege Man wechselt nicht und verliert. Spiel 6 Ziege Ziege Auto Man wechselt nicht und verliert.
-
In der zweiten Kolumne über das Thema „Ziegenproblem“ wurden außerdem die Leserbriefe von einigen Akademikern abgedruckt, die an vos Savant geschrieben und ihre Aussage in Zweifel gezogen hatten. Vos Savant beendete ihre zweite Kolumne zum Thema „Ziegenproblem“ mit den folgenden Worten:
„When you switch, you win 2/3 of the time and lose 1/3, but when you don’t switch, you only win 1/3 of the time and lose 2/3. You can try it yourself and see. Alternatively, you can actually play the game with another person acting as the host with three playing cards—two jokers for the goat and an ace for the prize. However, doing this a few hundred times to get statistically valid results can get a little tedious, so perhaps you can assign it as extra credit—or for punishment! (That’ll get their goats!)“
„Wenn Sie wechseln, gewinnen Sie in 2/3 aller Fälle und verlieren in 1/3 aller Fälle, doch wenn Sie nicht wechseln, gewinnen Sie lediglich in 1/3 aller Fälle und verlieren in 2/3 aller Fälle. Sie können es ja selbst ausprobieren. Als Alternative können Sie das Spiel mit jemand anderem, der die Rolle des Showmasters übernimmt, nachspielen. Dabei können Sie drei Spielkarten benutzen – zwei Joker für die Ziege und ein Ass für den Gewinn. Allerdings müsste man, um statistisch korrekte Ergebnisse zu erhalten, dieses Spiel ein paar hundert Mal durchspielen, was meiner Meinung nach ein wenig ermüdend werden könnte. Deswegen können Sie dies als eine Ehrenrunde betrachten – oder als eine Bestrafung! (Dann werden wir sehen, wer hier die Ziege ist!)“
In der dritten „Ziegenproblem“-Kolumne vom 17. Februar 1991[38] publizierte vos Savant den Prozentansatz der Leser, die ihre Aussage für falsch hielten. Sie betonte, dass die Tatsache, dass der Showmaster stets absichtlich eine Tür mit einer Ziege öffnet, der wichtigste Punkt sei.
„The original answer is still correct, and the key to it lies in the question, “Should you switch?” Suppose we pause at that point, and a UFO settles down onto the stage. A little green woman emerges, and the host asks her to point to one of the two unopened doors. The chances that she’ll randomly choose the one with the prize are 1/2, all right. But that’s because she lacks the advantage the original contestant had—the help of the host. (Try to forget any particular television show.) When you first choose door #1 from three, there’s a 1/3 chance that the prize is behind that one and a 2/3 chance that it’s behind one of the others. But then the host steps in and gives you a clue. If the prize is behind #2, the host shows you #3, and if the prize is behind #3, the host shows you #2. So when you switch, you win if the prize is behind #2 or #3. You win either way! But if you don’t switch, you win only if the prize is behind door #1. And as this problem is of such intense interest, I’m willing to put my thinking to the test with a nationwide experiment. This is a call to math classes all across the country.“
„Die ursprüngliche Antwort ist noch immer korrekt, und der Schlüssel liegt in der Frage, ob man wechseln sollte. Nehmen wir an, dass wir an dieser Stelle eine Pause machen, und dass ein UFO auf der Bühne landet. Eine kleine grüne Frau erscheint, und der Showmaster bittet sie, auf eine der beiden noch ungeöffneten Türen zu zeigen. Die Wahrscheinlichkeit, daß sie zufällig die mit dem Preis auswählen wird, beträgt 1/2, in Ordnung. Aber das liegt daran, daß sie den Vorteil des ursprünglichen Kandidaten nicht hat – die Hilfe des Showmasters. (Versuchen Sie, jegliche Fernsehshows zu vergessen.) Wenn Sie zuerst Tür Nummer eins wählen, haben Sie eine Chance von 1/3, dass der Preis dahinter steckt. Die Wahrscheinlichkeit, dass der Preis hinter einer der beiden anderen Türen versteckt ist, beträgt 2/3. Dann schreitet jedoch der Showmaster ein und gibt Ihnen einen Tipp. Wenn der Preis sich hinter Tür Nummer zwei befindet, wird er Tür Nummer drei öffnen, und wenn der Preis hinter Tür Nummer drei versteckt ist, wird er die zweite Tür öffnen. Wenn Sie also wechseln, gewinnen Sie, wenn der Preis entweder hinter der zweiten oder der dritten Tür steht. Sie gewinnen so oder so! Wenn Sie jedoch nicht wechseln, gewinnen Sie nur, wenn der Preis hinter Tür Nummer eins steht. Und da dieses Problem so viel Interesse geweckt hat, bin ich bereit, meine Gedanken durch ein landesweites Experiment auf ihre Richtigkeit überprüfen zu lassen. Dies ist ein Aufruf an alle möglichen Mathematikklassen im ganzen Land.“
Vos Savant beendete ihre dritte Kolumne über dieses Thema, indem sie Schüler dazu aufrief, das „Ziegenproblem“ nachzuspielen, die Ergebnisse und Statistiken zu notieren und diese ihr anschließend zuzusenden.
In ihrer vierten und letzten Kolumne über das „Ziegenproblem“ vom 7. Juli 1991[38] enthüllte vos Savant, dass ein großer Teil ihrer Leser nun von der Richtigkeit ihrer ursprünglichen Aussage überzeugt sei und viele ihrer Bitte nachgekommen seien, das „Ziegenproblem“ konkret nachzuspielen. 71 % der Akademiker und 56 % der restlichen Absender seien nun von ihren Argumenten überzeugt. Manche hätten ihr auch gestanden, dass sie aus der Affäre viel gelernt hätten, vor allem viel über die durchschnittlichen mathematischen Kenntnisse amerikanischer Bürger.[35] Marilyn vos Savant selbst hatte dazu gesagt: „Lösungen mathematischer Probleme werden nicht durch Abstimmung entschieden.“[39]
Sowohl Psychologen vom Berliner Max-Planck-Institut für Bildungsforschung[34] als auch Mitarbeiter des Massachusetts Institute of Technology sind durch eigene Experimente zu derselben Schlussfolgerung wie Marilyn vos Savant gekommen. Darüber hinaus waren auch die Reaktionen, die sie seitens vieler Schulen erhielt, weitgehend positiv.
Vos Savant erläuterte das „Ziegenproblem“ nicht nur in vier verschiedenen Ausgaben ihrer Kolumne „Ask Marilyn“, sondern auch in hunderten von Zeitungsartikeln. Nachdem die Richtigkeit ihrer Aussage von der Öffentlichkeit allgemein anerkannt worden war, entschuldigten sich die meisten derjenigen, die eine andere Lösung für richtig gehalten hatten, für die Argumente und Formulierungen, die sie in ihren Briefen verwendet hatten. Vos Savant selbst sagte in Bezug auf die Briefe, deren Absender sie von der angeblichen Falschheit ihrer Aussage überzeugen wollten: „Das Ganze hat mir unglaublich viel Spaß bereitet. Ich habe diese gehässigen Briefe, die ich damals erhalten habe, sehr genossen. Was für eine Dreistigkeit manche Leute doch an den Tag legen! Ich habe sie regelrecht verschlungen.“[8]
Das „Ziegenproblem“ wurde noch mehrere Jahre nach der Debatte über Marilyn vos Savants Lösungsweg in den Medien besprochen. Zum Beispiel urteilte Ernst Horst im Oktober 2000 in der Frankfurter Allgemeinen Zeitung über das „Ziegenproblem“: „Viele Akademiker mit beeindruckenden Titeln haben sich in diesem Zusammenhang vor einem Millionenpublikum der Lächerlichkeit preisgegeben. Das ändert aber nichts daran, daß das Dilemma im Grunde nur eine Bagatelle ist und man sich schleunigst mit wichtigeren Dingen beschäftigen sollte.“[40] Auch in „Ask Marilyn“ wird dieses Thema noch heute manchmal aufgegriffen. So wurde im Oktober 2009 in der virtuellen Ausgabe der Kolumne ein Leserbrief veröffentlicht, dessen Absender vos Savant unter anderem für die Beharrlichkeit, die sie während der Diskussion über das „Ziegenproblem“ gezeigt hatte, lobt.[41]
Diskussion über Marilyn vos Savants Intelligenzquotient
In Bezug auf Marilyn vos Savants Intelligenzquotienten werden je nach Quelle verschiedene IQ-Werte genannt. Diese variieren zwischen 167+, 186, 218, 228 und 230, wobei der im Guinness-Buch der Rekorde erwähnte IQ von 228 der am häufigsten angegebene Wert ist. Vos Savant soll diesen Intelligenzquotienten erzielt haben, als sie als Mädchen dem Stanford-Binet-Test unterzogen wurde. Die Tatsache, dass man je nach Quelle auf verschiedene IQ-Werte stoßen kann, ist zum einen darauf zurückzuführen, dass vos Savant im Laufe ihres Lebens mehreren Intelligenztests unterzogen wurde. Zum anderen sind sowohl der Zeitpunkt, an dem Marilyn vos Savant den Stanford-Binet-Test ablegte, als auch das Intelligenzalter, das sie damals erreichte, umstritten. Hingegen ist man sich darüber einig, dass vos Savant einen weit überdurchschnittlichen Intelligenzquotienten hat.
Vos Savant gibt an, dass sie im September 1956 als Schülerin an der Susan R. Buder School einer für Erwachsene erstellten Edition des Stanford-Binet-Tests unterzogen wurde. Sie erreichte in dieser Prüfung ein Maximum an Punkten. Dadurch soll vos Savant, die im September 1956 exakt zehn Jahre alt war, ein größtmögliches Intelligenzalter von 22 Jahren und zehn Monaten erreicht haben. Der Intelligenzquotient, den man dementsprechend aus ihrem Intelligenzalter und ihrem damaligen Lebensalter bildete, ergab einen Wert von 228.[8] Dieses Ergebnis liegt 8,53 Standardabweichungen oberhalb der Norm, wenn man von einem durchschnittlichen Wert von einhundert Punkten und einer Standardabweichung von fünfzehn Punkten ausgeht.[42] Über den Prozentrang von vos Savants Intelligenzquotienten von 228 sowie über die Wahrscheinlichkeit, mit der ein Individuum ein solches Resultat erzielt, herrscht jedoch ebenfalls keine Einigkeit, da es bei einem hohen Intelligenzquotienten schwierig ist, diese Werte annähernd zu bestimmen. Der britische Psychologe Andrew M. Colman behauptet, die Wahrscheinlichkeit, dass ein zufällig ausgewählter Mensch einen IQ von 228 hat, betrage weniger als eins zu 100 Billiarden.[43] Der Informatiker Jud McCranie hingegen geht davon aus, dass ein IQ von 197 einer Seltenheit von eins zu sechs Milliarden entspricht. Dementsprechend sei ein Mensch mit einem IQ von 228 unter ungefähr 9,8 Billiarden nur einmal vorzufinden.[44]
Die Informationen, die man vos Savants schulischen Akten entnehmen kann, sind zum Teil widersprüchlich. So dokumentieren diese auf der einen Seite, dass vos Savant den Stanford-Binet-Test nicht im September 1956, sondern im März 1957 ablegte. Auf der anderen Seite steht in den Akten, dass Marilyn vos Savant zu dem Zeitpunkt, an dem sie diese Prüfung ablegte, zehn Jahre und acht Monate alt war. Sie erreichte, da sie die volle Punktzahl erzielt hatte, ein Intelligenzalter von mindestens siebzehn Jahren und zehn Monaten, was einem IQ von 167+ entsprach. Dieser Wert wurde auch für vos Savants Beitritt zu Mensa International verwendet.[7] Im März 1957 kann vos Savant jedoch höchstens zehn Jahre und sieben Monate alt gewesen sein.
Unumstritten ist hingegen, dass vos Savant im Alter von sieben Jahren und sieben Monaten zum ersten Mal einem Intelligenztest unterzogen wurde. Zusammen mit einigen anderen Klassenkameraden erreichte sie die volle Punktzahl, was allerdings nur einem IQ von 127 entsprach.[7] Außerdem wurde sie auch als Acht- und Neunjährige jeweils einmal einem IQ-Test unterzogen, wobei sie jedes Mal ebenfalls die größtmögliche Punktezahl bekam.[8][45]
Schließlich kontaktierte Marilyn vos Savant den amerikanischen Philosophen Ronald K. Hoeflin, der mehrere Hochbegabtenclubs, darunter die Mega Society, gegründet hatte. Nach Hoeflins Aussage hatte vos Savant ihm erklärt, dass sie auf dem Stanford-Binet-Test als Zehnjährige die volle Punktzahl erreicht hätte. Hoeflin berechnete vos Savants IQ, indem er ein Intelligenzalter von 22 Jahren und elf Monaten durch ein Lebensalter von zehn Jahren und sechs Monaten dividierte. Dies entsprach einem Intelligenzquotienten von 218.[7] Allerdings betrug das größtmögliche Intelligenzalter, das der Stanford-Binet-Test erfassen konnte, nicht 22 Jahre und elf Monate, sondern 22 Jahre und zehn Monate. Außerdem war Marilyn vos Savant weder im September 1956 noch im März 1957 zehn Jahre und sechs Monate alt.
1985 nahm vos Savant am „Mega-Test“ teil, der von Ronald K. Hoeflin speziell für Hochbegabte konzipiert worden war. Bei diesem Test erreichte vos Savant 46 von 48 Rohpunkten, was einem Intelligenzquotienten von 186 entsprach. Den von Hoeflin aufgestellten Statistiken zufolge liegt dieser Wert 5,4 Standardabweichungen oberhalb der Norm und entspricht einem Prozentrang von 99,999997 %, so dass theoretisch nur einer von dreißig Millionen Menschen ein solches Resultat erzielt.[46] Die Redaktion des Guinness-Buches der Rekorde konnte von diesem Ergebnis Notiz nehmen, als der Bostoner Anwalt Andrew Egendorf, der ein Buch über Hochbegabtenclubs verfasste, mit vos Savant Kontakt aufnahm und ihre Testergebnisse an die Redaktion des Guinness-Buches schickte.[9] Daraufhin stand vos Savant in den von 1986 bis 1989 veröffentlichten Ausgaben des Guinness-Buches mit ihren beiden Intelligenztestwerten von 228 und 186 unter der Rubrik „höchster IQ“. Seit diese Kategorie für spätere Editionen aus dem Guinness-Buch der Rekorde jedoch entfernt wurde, wird vos Savant unter derselben Rubrik in der „Guinness Book of World Records Hall of Fame“ erwähnt.[33] Bevor Marilyn vos Savants Ergebnisse in das Guinness-Buch der Rekorde eingetragen wurden, wurde dort ein IQ von 196 als der höchste je gemessene Intelligenzquotient weltweit aufgelistet.[7]
Ronald K. Hoeflin ging bei der Berechnung von vos Savants Intelligenzquotienten von einer Standardabweichung von sechzehn Punkten aus,[46] so dass die beiden Werte von 228 und 186 auf verschiedenen Skalen gemessen wurden. Auf der für den „Mega-Test“ verwendeten Skala entspräche vos Savants Stanford-Binet-Wert von 228 einem Intelligenzquotienten von 188. Hingegen entspräche der IQ-Wert von 186, den sie beim „Mega-Test“ erzielte, auf der Skala des Stanford-Binet-Tests einem Wert von 224.[47]
Manchmal wird anstelle des IQs von 228 ein gerundeter Wert von 230 verwendet. Dieser Wert wird zum Beispiel von Marilyn vos Savants 1990 erschienenem Ratgeber „Brain Building“ angegeben.[48]
Marilyn vos Savant ist der Ansicht, dass IQ-Tests selbst dann primitive Messinstrumente von Intelligenz seien, wenn man sich ihnen von einem professionellen Prüfer unterziehen ließe. Sie vertritt den Standpunkt, dass jemandes Intelligenz von so vielen Faktoren geprägt werde, dass jeglicher Versuch, Intelligenz zu messen, nutzlos sei. Dennoch seien IQ-Tests nicht vollkommen unnütz: Tests von guter Qualität erfassen verschiedene geistige Fähigkeiten, Intelligenz selbst könnten sie jedoch nicht messen.[49]
Trotz ihrer überdurchschnittlichen Testwerte halte sie sich nicht für klüger als ihre Mitmenschen, so vos Savant.[14]
Rezeption in der Öffentlichkeit
Seit Marilyn vos Savant Mitte der 1980er Jahre ins Guinness-Buch der Rekorde unter der Kategorie „höchster Intelligenzquotient“ eingetragen wurde, sind Stimmen laut geworden, die fragen, weshalb vos Savant mit ihrem hohen IQ sich auf das Schreiben einer Magazinkolumne beschränkt[8] und keine Karriere als Naturwissenschaftlerin, Politikerin oder Künstlerin eingeschlagen hat. So stellte Walter Goodman in der New York Times in einem Artikel von September 1998 die Frage, warum Marilyn vos Savant nicht für das Memorial Sloan-Kettering Cancer Center oder das Außenministerium der Vereinigten Staaten arbeitet.[50] Im März 1999 stellten Lynn Harris und J. D. Heiman von derselben Zeitung anlässlich des bevorstehenden Jahrtausendwechsels eine Liste der unwichtigsten Nachrichten des 20. Jahrhunderts auf. Die Nachricht, dass Marilyn vos Savant vom Guinness-Buch der Rekorde 1986 als die „klügste Frau der Welt“ bezeichnet worden war, wurde auf Platz 14 gewählt.[2]
1995 kreierte Herb Weiner, ein Softwaretechniker aus Portland in Oregon, die Website „Marilyn is Wrong!“, in der er Fehler herausgreift, die vos Savant seiner Ansicht nach beim Beantworten ihrer Leserfragen gemacht hat. Er begründete seine Initiative damit, dass er sichergehen wolle, dass vos Savants Antworten nicht fraglos akzeptiert werden. Weiner hat seine Verwunderung darüber, dass vos Savant überhaupt eine Kolumne verfasst, in einem 2009 in der Financial Times erschienenen Artikel in folgende Worte gefasst: „Schauen Sie sich Barack Obama an, schauen Sie sich an, wie er seine Intelligenz nutzt. Es wundert mich, dass sie sich kaum mit komplexen Angelegenheiten beschäftigt, sondern meistens lediglich Rätsel löst oder simple Fragen beantwortet, die jeder nach ein bisschen Recherche selbst beantworten könnte.“[8]
Ähnliche Gedanken äußerte auch die amerikanische Psychologin Ellen Winner in ihrem 1996 erschienenen Fachbuch „Hochbegabt – Mythen und Realitäten von außergewöhnlichen Kindern“. Sie schrieb: „Der eigentliche Grund, weshalb ein hoher IQ in der Kindheit keine Vorhersagen über die künftige Kreativität erlaubt, liegt sicher darin, daß Intelligenz und Kreativität zwei grundverschiedene Dinge sind. […] Ein Mensch kann hochintelligent sein, aber trotzdem starr, unkreativ und ohne die leiseste Spur jener zielstrebigen Leidenschaft, die kreative Menschen antreibt. Nehmen wir das oft zitierte Beispiel von Marilyn Jarvik (geborene vos Savant), die mit dem höchsten je gemessenen IQ von 228 ins Guiness-Buch [sic] der Rekorde eingegangen ist. Heute schreibt sie eine Kolumne mit dem Titel ‚Frag Marilyn‘ für eine Sonntagszeitung und antwortet Lesern, die sie mit kniffligen Fragen austricksen wollen. Sie mag schnell sein, sie mag klug sein, aber niemand würde sie als besonders schöpferisch im Sinne einer großen Kreativität bezeichnen.“[51]
In vos Savants Kolumne wurde die Frage, weshalb sie sich niemals einer Karriere als Naturwissenschaftlerin gewidmet hätte, ebenfalls aufgegriffen. Im November 2009 wurde vos Savant von einer Leserin gefragt, warum sie sich für eine solche Karriere nicht entschieden hätte, wo sie doch ihrer hohen Intelligenz schon von früher Kindheit an bewusst gewesen wäre. Marilyn vos Savant erwiderte darauf, dass sie sich für eine solche Berufsausbildung nicht interessiert hätte, und dass es bereits genügend intelligente Menschen gäbe, die im naturwissenschaftlichen Bereich tätig seien.[52]
Darüber hinaus ist die vom Guinness-Buch der Rekorde erstmals aufgestellte Behauptung, Marilyn vos Savant sei der intelligenteste Mensch der Welt und habe einen IQ von 228, von verschiedenen Seiten in Frage gestellt worden. Veith Tiemann, der sich in seinem Buch „Einführung Statistik“ unter anderem mit dem „Ziegenproblem“ beschäftigte, schrieb hierzu Folgendes: „Eine zusätzliche – vielleicht auch die ausschlaggebende – Brisanz erfuhr die Angelegenheit durch die Tatsache, daß Frau Savant die zweifelhafte Auszeichnung Mensch mit dem höchsten IQ zuteil wurde. Die Aussage an sich schreit bereits nach Widerspruch und hat kaum eine realistische Chance, der Wahrheit zu entsprechen.“[53] Auch Andrew M. Colman und Jud McCranie halten es statistisch gesehen für unmöglich, dass vos Savant einen Intelligenzquotienten von 228 haben kann. Sie argumentieren, dass es viel zu wenig Menschen gebe, um auf der Erde jemanden mit einem derart hohen IQ zu finden.[43][44]
Olle Häggström, Professor für mathematische Statistik an der Technischen Hochschule Chalmers,[54] hat angesichts der Behauptung, Marilyn vos Savant habe den höchsten Intelligenzquotienten der Welt, in seinem Buch „Streifzüge durch die Wahrscheinlichkeitstheorie“ ebenfalls Zweifel geäußert: „Ich bin bezüglich dieser Behauptung etwas skeptisch. Wie kann eine Person wissen, dass sie den höchsten IQ der Welt besitzt? Und wenn jemand der intelligenteste Mensch der Welt ist, ist es dann wirklich vernünftig, diese einzigartige Ressource für eine Fragekolumne in einer wenig fortschrittlichen Zeitschrift zu verwenden?“[55]
Auszeichnungen
1998 wurde vos Savant vom Weißen Haus aufgrund ihrer Bemühungen zur Veränderung der Verhaltensmuster gegenüber Frauen als eine von fünfzig „Frauen des neuen Jahrtausends“ bestimmt. Außerdem wurde ihr aus demselben Grund der „Women Making History“-Award von dem „National Women’s History“-Museum verliehen.[56] Darüber hinaus wurde ihr am 17. Mai 2003 vom College of New Jersey ein Ehrendoktor in Literaturwissenschaften verliehen.[57] Toastmasters bezeichnete vos Savant als einer der „Five Outstanding Speakers of 1999“.[4]
Zitate
„People expect me to be a walking encyclopaedia or a human calculator, or to have very unusual, very esoteric, very arcane gifts and I’m really not that way at all.“
„Die Leute erwarten von mir, dass ich wie ein wandelndes Lexikon oder eine Kopfrechenmaschine auftrete, oder sie schreiben mir außergewöhnliche, geheimnisvolle, übernatürliche Fähigkeiten zu. Über solche Fähigkeiten verfüge ich jedoch keineswegs.“
– Marilyn vos Savant: 2009, zitiert in einem Artikel der Financial Times
„Marilyn vos Savant believes success in life depends more on social skills than on intellectual skills. [...] Marilyn vos Savant has a wide mind. She says she knows things in many fields and is like a “conductor rather than a violinist.” She is good at systems analysis, has an excellent visual memory, and is very good at logic. She has no idiot-savant skills at all—no photographic memory, no ability to remember statistics or compute long sums in her head. She says she is best at “objective synoptical analysis,” making decisions, problem solving, critical thinking, and analysis.“
„Marilyn vos Savant zufolge ist Erfolg im Leben mehr von sozialem Geschick als von intellektuellen Fähigkeiten abhängig. [...] Marilyn vos Savant besitzt einen offenen Geist. Sie sagt, sie wisse über viele Themen Bescheid und gliche „mehr einem Dirigenten als einem Violinisten“. Sie verfügt über eine gewisse Begabung auf dem Gebiet der Systemanalyse sowie über ein ausgezeichnetes visuelles Gedächtnis und ist gut im logischen Denken. Sie hat keinerlei Inselbegabungen – sie hat kein fotografisches Gedächtnis, kann sich keine komplizierten Statistiken merken und auch keine enormen Summen im Kopf ausrechnen. Sie behauptet, „objektive synoptische Analysen“, das Treffen von Entscheidungen, das Lösen von Problemen, kritisches Denken und Analysieren liegen ihr am meisten.“
– Julie Baumgold: „In the Kingdom of the Brain“, New York Magazine, 1989
Bezüge in der Popkultur
In „Die Stadt der primitiven Langweiler“ (im Original „They Saved Lisa’s Brain“), der am 9. Mai 1999 erstmals gesendeten 225. Episode der US-amerikanischen Zeichentrickserie „Die Simpsons“, wird erzählt, wie die intellektuell frühreife Lisa Simpson in den Hochbegabtenclub Mensa International aufgenommen wird. Anlässlich ihrer Aufnahme in den Club wird sie durch eine Galerie geführt, in der die Portraits einiger Mitglieder von Mensa hängen. Darunter befindet sich neben einem Bild der Schauspielerin Geena Davis und des Comiczeichners Mell Lazarus auch eines von Marilyn vos Savant.
In dem 2003 von Mark Haddon veröffentlichten Roman „Supergute Tage oder die sonderbare Welt des Christopher Boone“ beschäftigt sich der mathematisch höchstbegabte Protagonist Christopher Boone, bei dem das Asperger-Syndrom diagnostiziert wurde, an einer Stelle mit dem von Marilyn vos Savant behandelten „Ziegenproblem“. Boone erklärt, dass die meisten Menschen von ihrer Intuition zu einer falschen Lösung des „Ziegenproblems“ verleitet würden. Er fügt hinzu, dass die Intuition generell zu Fehlern verführe, während der Einsatz von Logik einem zu korrekten Schlussfolgerungen verhelfe. Allerdings würde gerade die Intuition von den meisten Leuten beim Treffen ihrer Entscheidungen eingesetzt.[58]
Werke
- 1985: Omni I.Q. Quiz Contest, McGraw-Hill, ISBN 0-07-039377-X
- 1988: It Was Poppa’s Will, Bühnenstück
- 1990: Brain Building: Exercising Yourself Smarter (mit Koautorin Leonore Fleischer), Bantam Books, ISBN 0-553-35348-9
- 1992: Ask Marilyn: Answers to America’s Most Frequently Asked Questions, St. Martin’s Press, ISBN 0-312-08136-7
- 1993: The World’s Most Famous Math Problem: The Proof of Fermat’s Last Theorem and Other Mathematical Mysteries, St. Martin’s Press, ISBN 0-312-10657-2
- 1994: Ask Marilyn: The World’s Smartest Woman Answers America’s Most Difficult Questions, St. Martin’s Press, ISBN 0-312-95181-7
- 1994: More Marilyn: Some Like It Bright!, St. Martin’s Press, ISBN 0-312-11384-6
- 1994: “I’ve Forgotten Everything I Learned in School!”: A Refresher Course to Help You Reclaim Your Education, St. Martin’s Press, ISBN 0-312-10457-X
- 1996: Of Course I’m for Monogamy: I’m Also for Everlasting Peace and an End to Taxes, St. Martin’s Press, ISBN 0-312-16951-5
- 1996: The Power of Logical Thinking: Easy Lessons in the Art of Reasoning … and Hard Facts about Its Absence in Our Lives, St. Martin’s Press, ISBN 0-312-15627-8
- 2000: The Art of Spelling: The Madness and the Method, W. W. Norton & Company, Inc., ISBN 0-393-32208-4
- 2002: Growing Up: A Classic American Childhood, W. W. Norton & Company, Inc., ISBN 0-393-05125-0
Außerdem hat Marilyn vos Savant eine Sammlung humoristischer Kurzgeschichten,[12] eine politische Satire mit dem Titel „The New Patriot“ sowie „The Re-Creation“ verfasst. Bei „The Re-Creation“ handelt es sich um eine satirische Darstellung aller klassischen Zivilisationen.[7]
Weblinks
- Literatur von und über Marilyn vos Savant im Katalog der Deutschen Nationalbibliothek
- Marilyn vos Savant in der Notable Names Database (englisch)
- Offizielle Website (engl.)
- Online-Version von „Ask Marilyn“ (engl.)
- Marilyn is Wrong! (engl.), von Herb Weiner aufgestellte Website
- Interview mit Marilyn vos Savant auf YouTube, Februar 1986
Presse
- „The cleverest person answers your questions“ (engl.), Financial Times, 30. Mai 2009
- Sam Knight: „Is a high IQ a burden as much as a blessing?“ (engl.), Financial Times, 10. April 2009
- Jochen Paulus: „Das Rätsel der drei Türen“, Die Zeit, 18. November 2004
- John Allen Paulos: „In Short: Nonfiction“ (engl.), New York Times, 16. Januar 1994
- Julie Baumgold: „In the Kingdom of the Brain“ (engl.), New York Magazine, 6. Februar 1989
Quellenangaben und Fußnoten
- ↑ „Nonverbal rückwärts einparken“, Frankfurter Allgemeine Zeitung, 23. Oktober 2005
- ↑ a b Lynn Harris, J. D. Heiman: „Ideas & Trends; You Must Remember This. Never Mind.“ (engl.), New York Times, 7. März 1999
- ↑ Chase’s Calendar of Events 2009 (engl.), McGraw-Hill, 2008, ISBN 978-0-07-159954-2; S. 402
- ↑ a b c About Marilyn (engl.)
- ↑ a b c Marilyn vos Savant in der NNDB (engl.)
- ↑ Parade.com – Ask Marilyn (engl.), Ausgabe vom 14. November 2007
- ↑ a b c d e f g h Julie Baumgold: „In the Kingdom of the Brain“ (engl.), New York Magazine, 6. Februar 1989
- ↑ a b c d e f g h i j k Sam Knight: „Is a high IQ a burden as much as a blessing?“ (engl.), Financial Times, 10. April 2009
- ↑ a b c d e Semana.com – „Coeficiente intelectual: 228“ (Spanisch), Semana, 6. Juni 2009
- ↑ „The cleverest person answers your questions“ (engl.), Financial Times, 30. Mai 2009
- ↑ a b Ask Marilyn – „A Nom de Plume?“ (engl.), Ausgabe vom 8. Dezember 2009
- ↑ a b c Marilyn vos Savant, Leonore Fleischer: Brain Power – The 12-Week Mental Training Programme (engl.); Verlag Piatkus, London 2005, ISBN 0-7499-2555-8, S. 2
- ↑ Samuel E. Wood, Ellen Green Wood, Denise Boyd: The World of Psychology (engl.), Prentice Hall, 2010, ISBN 978-0-205-76373-3, S. 262
- ↑ a b c Andrew York: „Marilyn vos Savant y la lógica“ (Spanisch), La revista Mercedes, Sommer 2007; S. 52f.
- ↑ Mary T. Schmich: „She Outsmarts the Human Race with an IQ of 230, Woman’s One of a Kind“ (engl.), Chicago Tribune, 8. Oktober 1985
- ↑ A. Sardón: Marilyn vos Savant: „Para tener éxito es más importante saber relacionarse que ser inteligente“ (Spanisch), Muy Interesante, November 1995
- ↑ YouTube: “Marilyn Mach Vos Savant – Feb. 1986 Air date”: “Actually, I’ve lived under a pseudonym for many years now. […] That’s because I was writing, and I wanted to avoid possible premature publication. I wanted to get decent enough before the work was published.”
- ↑ Younglove, Dennis FIDE Chess Profile – Players Arbiters Trainers (engl.)
- ↑ Working Mother – „Some Fathers Know Best“ (engl.), Juli 1987
- ↑ Robert Jarvik in der Internet Movie Database
- ↑ a b Michael Vitez: „World’s Smartest Couple Robert Jarvik, Marilyn Vos Savant Both Married Into Brains“ (engl.), KNT News Service, 5. Juli 1988
- ↑ The Daily Miscellany – August 23 (engl.); im Internet Archive
- ↑ Mitunter wird irrtümlicherweise behauptet, dass Marilyn vos Savants Kinder, Mary und Dennis, aus ihrer Ehe mit Robert Jarvik stammen.
- ↑ Stephanie Saul: „Artificial heart inventor returns to spotlight - and controversy“ (engl.), New York Times, 6. Februar 2008
- ↑ a b Mary Jane Sterling: Math Word Problems for Dummies (engl.), For Dummies, 2007, ISBN 978-0-470-14660-6, S. 319
- ↑ Melissa Balmain Weinter: „Her Workout: Mental Push-ups to Fight Brain Drain“ (engl.), Orange County Register, 5. April 1990
- ↑ Bob McTeer: „The Dismal Science? Hardly!“ (engl.), Wall Street Journal, 4. Juni 2003
- ↑ Ron Yannone: „Pending Inquiry to Marilyn vos Savant on Publishing the Titan Test in Parade Magazine“ (engl.), veröffentlicht in Noesis – The Journal of the Mega Society am 3. Januar 2006
- ↑ About the Mega Society (engl.)
- ↑ Facts on Parade (engl.)
- ↑ Parade.com – Marilyn’s Weekly Quiz (engl.)
- ↑ Parade.com – About Numbrix (engl.)
- ↑ a b „Ask Marilyn“ by Marilyn vos Savant – Parade (engl.)
- ↑ a b c „Das Rätsel der drei Türen“, Die Zeit, 18. November 2004
- ↑ a b c d e Marilyn vos Savant.com – Game Show Problem (engl.)
- ↑ John Tierney: „Behind Monty Hall’s Doors: Puzzle, Debate and Answer?“ (engl.), New York Times, 21. Juli 1991
- ↑ Heinrich Hemme: Die Sphinx. 93 mathematische Rätsel mit ausführlichen Lösungen, Vandenhoeck & Ruprecht, 1994, ISBN 978-3-525-40735-6, S. 60
- ↑ a b c Morton Ann Gernsbacher, Sharon J. Derry: Proceedings of the Twentieth Annual Conference of the Cognitive Science Society, Psychology Press, 1998, ISBN 978-0-8058-3231-0, S. 18
- ↑ Grundlegende Vorstellungen der Informationsmathematik – Bertrands Schachtelparadoxon oder „die Magie der Information“
- ↑ Ernst Horst: „Im Land der Mathemagie – Die klügste Frau der Welt bittet zum Kolleg“, Frankfurter Allgemeine Zeitung, 11. Oktober 2000
- ↑ Ask Marilyn – „Monty and the Goats“ (engl.), Ausgabe vom 7. Oktober 2009
- ↑ Andrew M. Colman, David D. Stretch: „Paranormal IQ Scores?“ (engl.)
- ↑ a b Andrew M. Colman: „A supernatural IQ? Investigating a claim to an extraordinary IQ“ (engl.), 1993
- ↑ a b Herb Weiner: Comments on Marilyn’s IQ (engl.), 3. Oktober 1998
- ↑ Dennis Coon, John O. Mitterer: Psychology: A Journey (engl.), Wadsworth Publishing, 2007, ISBN 978-0-495-09553-8; S. 305
- ↑ a b The Sixth Norming of the Mega Test (engl.) von Ronald K. Hoeflin
- ↑ John Scoville: Statistical Distribution of Childhood IQ Scores (engl.)
- ↑ Marilyn vos Savant, Leonore Fleischer: Brain Power – The 12-Week Mental Training Programme; Verlag Piatkus, London 2005; ISBN 0-7499-2555-8: Marilyn vos Savant has an IQ of 230, one of the highest ever recorded.
- ↑ Ask Marilyn – „Are Men Smarther Than Women?“ (engl.), Ausgabe vom 17. Juli 2005
- ↑ Walter Goodman: „Critic’s Notebook; What Passes for News at 11 p.m.: High, Low and Sly“ (engl.), New York Times, 10. September 1998
- ↑ Ellen Winner: Hochbegabt – Mythen und Realitäten von außergewöhnlichen Kindern, ISBN 3-608-94160-6, Klett-Cotta, Stuttgart 1998, S. 260
- ↑ Ask Marilyn – „Science as a Career“ (engl.), Ausgabe vom 13. November 2009
- ↑ Veith Tiemann: Einführung Statistik, Gabler, 2003, ISBN 978-3-409-12407-2, S. 190
- ↑ cs.chalmers.se – Olle Häggström
- ↑ Olle Häggström: Streifzüge durch die Wahrscheinlichkeitstheorie, Springer 2005, ISBN 978-3-540-23050-2, S. 19
- ↑ First Annual „Women Making History“ Awards (engl.)
- ↑ „President’s Report to the Board“ von Präsidentin R. Barbara Gitenstein, 30. Juni 2003
- ↑ Mark Haddon: The Curious Incident of the Dog in the Night-time (engl.), Vintage 2004, ISBN 0-09-947043-8, S. 78-82
Kategorien:- Hochbegabung
- Rekordhalter
- US-amerikanischer Journalist
- Autor
- Person (St. Louis)
- Geboren 1946
- Frau
-
Wikimedia Foundation.