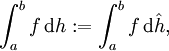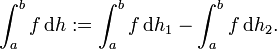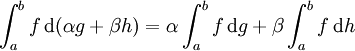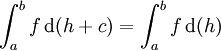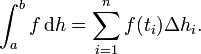- Lebesgue-Stieltjes-Integral
-
In der Integralrechnung bezeichnet das Stieltjesintegral eine wesentliche Verallgemeinerung des Riemannintegrals oder eine Konkretisierung des Integralbegriffs von Lebesgue. Benannt wurde es nach dem niederländischen Mathematiker Thomas Jean Stieltjes (1856-1894). Das Stieltjes-Integral, für den der Begriff des Integrators grundlegend ist, findet Anwendung auf vielen Feldern, insbesondere in der Physik und der Stochastik.
Inhaltsverzeichnis
Das Riemann-Stieltjes-Integral für monotone Integratoren
Seien
![[a,b] \ne \emptyset](/pictures/dewiki/56/82b4b4bd2de1cbf3354d240ceef19913.png) ein reelles Intervall sowie
ein reelles Intervall sowie ![f,h\,\!: [a,b] \to \R](/pictures/dewiki/54/635869c6b84f4f6ba0aed8176e475061.png) zwei Funktionen, wobei
zwei Funktionen, wobei 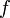 beschränkt sei.
beschränkt sei. 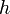 sei (nicht notwendigerweise streng) monoton wachsend. Das dazugehörige Riemann-Stieltjes-Integral von
sei (nicht notwendigerweise streng) monoton wachsend. Das dazugehörige Riemann-Stieltjes-Integral von 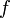 bezüglich
bezüglich 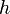 auf dem Intervall
auf dem Intervall ![[a,b]\!\,](/pictures/dewiki/98/bbef1ebf3a66625485811f5c547c3edc.png) wird wie das Riemannintegral über feine Zerlegungen des Intervalls, Ober- und Untersummen (siehe dort) definiert, jedoch lauten die Formeln der Ober- und Untersumme bei Stieltjes statt
wird wie das Riemannintegral über feine Zerlegungen des Intervalls, Ober- und Untersummen (siehe dort) definiert, jedoch lauten die Formeln der Ober- und Untersumme bei Stieltjes statt![\overline{S_N} = \sum_{i=1}^N \sup \Big\{ f(t):t \in [t_{i-1},t_i] \Big\} \cdot(t_i-t_{i-1})](/pictures/dewiki/101/ea3c5532dd0b337e06f162778709d43a.png) (Obersumme)
(Obersumme)
![\underline{S_N} = \sum_{i=1}^N \inf \Big\{ f(t):t \in [t_{i-1},t_i] \Big\} \cdot(t_i-t_{i-1})](/pictures/dewiki/101/e0c779d93d754008d2a6f88350312338.png) (Untersumme)
(Untersumme)
nun:
![\overline{S_N} = \sum_{i=1}^N \sup \Big\{ f(t):t \in [t_{i-1},t_i] \Big\} \cdot(h(t_i)-h(t_{i-1}))](/pictures/dewiki/98/be2e828e8a865db0583fa9c19757aeca.png) (Stieltjes-Obersumme)
(Stieltjes-Obersumme)
![\underline{S_N} = \sum_{i=1}^N \inf \Big\{ f(t):t \in [t_{i-1},t_i] \Big\}\cdot(h(t_i)-h(t_{i-1}))](/pictures/dewiki/57/9fa6f0a42e418c9b0f86f6fee0679477.png) (Stieltjes-Untersumme)
(Stieltjes-Untersumme)
Konvergieren Ober- und Untersumme für hinreichend feine Zerlegungen gegen denselben Wert, so heißt
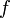 bezüglich
bezüglich 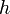 auf
auf ![[a,b]\!\,](/pictures/dewiki/98/bbef1ebf3a66625485811f5c547c3edc.png) Riemann-Stieltjes-Integrierbar und der gemeinsame Grenzwert wird als Wert des Integrals bezeichnet. Die Schreibweise hierfür ist:
Riemann-Stieltjes-Integrierbar und der gemeinsame Grenzwert wird als Wert des Integrals bezeichnet. Die Schreibweise hierfür ist:Die Funktion
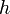 , auch als Integrator bezeichnet, regelt also, wie stark
, auch als Integrator bezeichnet, regelt also, wie stark 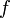 an verschiedenen Stellen gewichtet wird. Statt Integrator ist deshalb auch die Bezeichnung Gewichtsfunktion üblich. Offensichtlich kann das gewöhnliche Riemannintegral nun als Spezielfall des Riemann-Stieltjes-Integrals mit
an verschiedenen Stellen gewichtet wird. Statt Integrator ist deshalb auch die Bezeichnung Gewichtsfunktion üblich. Offensichtlich kann das gewöhnliche Riemannintegral nun als Spezielfall des Riemann-Stieltjes-Integrals mit 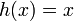 für alle
für alle 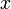 (Identität) aufgefasst werden.
(Identität) aufgefasst werden.Das Riemann-Stieltjes-Integral existiert z. B. bei stetiger Funktion
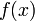 selbst mit der Cantor-Funktion als Integrator (das ist eine monoton von 0 auf 1 wachsende Funktion, die fast überall konstant ist, nämlich bis auf eine überabzählbare Nullmenge).
selbst mit der Cantor-Funktion als Integrator (das ist eine monoton von 0 auf 1 wachsende Funktion, die fast überall konstant ist, nämlich bis auf eine überabzählbare Nullmenge).Das Lebesgue-Stieltjes-Integral
Die Definition des Lebesgue-Stieltjes-Integrals fällt nicht schwer, da der monotonen Funktion h ein (fast überall) eindeutiges Maß
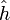 auf der Borelschen σ-Algebra
auf der Borelschen σ-Algebra ![\mathcal B([a,b])](/pictures/dewiki/98/b527b7bd8ace33c85bbcf386a7dfcf27.png) durch die Vorschrift
durch die Vorschriftzugeordnet werden kann (ist h die Identität, so handelt es sich um das Lebesgue-Maß). Ist f nun bezüglich dieses Maßes Lebesgue-integrierbar, so definiert man das zugehörige Lebesgue-Stieltjes-Integral als
wobei die rechte Seite als gewöhnliches Lebesgue-Integral aufzufassen ist.
Nicht-monotone Integratoren
Für eine eingeschränkte Menge nicht monoton wachsender Integratoren kann das Stieltjes-Integral ebenfalls sinnvoll definiert werden, nämlich für solche mit endlicher Variation auf
![[a,b]\,\!](/pictures/dewiki/56/8b596d04e319e05cadcc7dcf251a9815.png) . Funktionen endlicher Variation können nämlich stets als Differenz zweier monoton wachsender Funktionen dargestellt werden, also
. Funktionen endlicher Variation können nämlich stets als Differenz zweier monoton wachsender Funktionen dargestellt werden, also 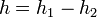 mit
mit ![h_1\!\,, h_2: [a,b] \to \R](/pictures/dewiki/50/22d1029e4d02bc5adb4e1381e090ae67.png) monoton wachsend. Das zugehörige Stieltjes-Integral (wahlweise im Riemannschen oder Lebesgueschen Sinne) ist dann definiert als
monoton wachsend. Das zugehörige Stieltjes-Integral (wahlweise im Riemannschen oder Lebesgueschen Sinne) ist dann definiert alsEs kann gezeigt werden, dass diese Definition sinnvoll, also unabhängig von der speziellen Wahl der Zerlegung ist.
Eigenschaften
- Falls zu
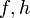 und
und ![[a,b]\,\!](/pictures/dewiki/56/8b596d04e319e05cadcc7dcf251a9815.png) das Riemann-Stieltjes-Integral existiert, so existiert auch das zugehörige Lebesgue-Stieltjes-Integral und die beiden Werte stimmen überein.
das Riemann-Stieltjes-Integral existiert, so existiert auch das zugehörige Lebesgue-Stieltjes-Integral und die beiden Werte stimmen überein.
- Die Linearität des Integrals im Integranden bleibt erhalten.
- Weiterhin ist das Stieltjesintegral auch linear im Integrator, also
- für Konstanten
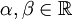 und Funktionen
und Funktionen 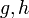 endlicher Variation.
endlicher Variation.
- Das Integral ist invariant unter Translationen des Integrators, also
- für Konstanten
 .
.
- Treppenfunktionen als Integratoren: Ist
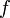 stetig und
stetig und 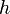 eine Treppenfunktion, die in den Punkten
eine Treppenfunktion, die in den Punkten ![t_1, \ldots, t_n \in\,]a,b[](/pictures/dewiki/49/17061280236a77f4e8396d338f739c81.png) Sprünge der Höhe
Sprünge der Höhe 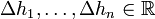 vollführt, so gilt
vollführt, so gilt
- Ist
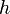 differenzierbar, so gilt
differenzierbar, so gilt
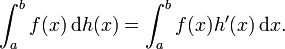
- (Im Lebesgueschen Sinne:
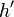 ist die Dichte von
ist die Dichte von 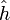 .)
.)
Literatur
I. P. Natanson: Theorie der Funktionen einer reellen Veränderlichen, Harri Deutsch Thun-Verlag, ISBN 3-87-144-217-8
Wikimedia Foundation.

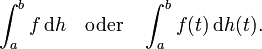
![\begin{align}
\hat h([x,y[)&:=h(y-)-h(x-),\\
\hat h([x,y])&:=h(y+)-h(x-)
\end{align}](/pictures/dewiki/50/29c2a5ca5d43a4a3780afaacc59f758b.png)