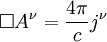- Kovariante Ableitung
-
Die kovariante Ableitung ist ein verallgemeinerter Ableitungsbegriff in nahezu beliebigen Räumen, genauer gesagt in differenzierbaren Mannigfaltigkeiten. Die kovariante Ableitung bedarf zu ihrer Definition einer zusätzlichen, räumlich veränderlichen Größe, des Zusammenhangs.
Der Zusammenhang definiert letzten Endes implizit die Krümmung des betrachteten Raumes, d.h. man kann über die Krümmung eines mathematischen Raums ohne verfügbaren Zusammenhang keinerlei Aussagen treffen. Andererseits bedeutet das Vorhandensein eines Zusammenhangs nicht notwendig eine Krümmung des Raums. Auch durch Verwendung krummliniger Koordinaten kann in einem ungekrümmten Raum ein Zusammenhang nötig werden.
Das Fachgebiet, welches der Untersuchung differenzierbarer Mannigfaltigkeiten gewidmet ist, ist die Differentialgeometrie.
Ihre wichtigsten physikalischen Anwendungen findet die kovariante Ableitung in der Geodäsie, also der Vermessung der Erdoberfläche und der allgemeinen Relativitätstheorie. In solchen im anschaulichen Sinne geometrischen Anwendungen kann die kovariante Ableitung auf eine Metrik, also ein lokales Maß für die Länge von Vektoren und damit Wegen im Raum, zurückgeführt werden. Im allgemeineren Fall muss es jedoch nicht immer eine Metrik geben, aus der sich der Zusammenhang ergibt. Dies ist zum Beispiel bei ihrer abstrakteren Anwendung in den Eichfeldtheorien der Elementarteilchenphysik der Fall.
In praktischer Hinsicht wird der Zusammenhang eines gegebenen physikalischen Raums durch Wahl eines bestimmten Koordinatensystems und darin durch Messung bestimmt, so etwa bei der Geodäsie. Es kann in bestimmten Fällen auch zu Mehrdeutigkeiten kommen, wenn nämlich die betrachteten physikalischen Größen nicht direkt messbar sind. Dies ist eben der Fall in den Eichfeldtheorien. So sind etwa die Phase der quantenmechanischen Wellenfunktion und das elektromagnetische Vektorpotenzial keine direkt messbaren Größen.
Inhaltsverzeichnis
Physikalische Motivation
Der Grundgedanke, welcher die Definition der kovarianten Ableitung motiviert, kann am einfachsten anhand einer zweidimensionalen gekrümmten Fläche im dreidimensionalen Raum, einem Einbettungsraum für die Fläche, erläutert werden. Das gängigste Beispiel einer solchen Fläche ist die Erdoberfläche oder näherungsweise eine Kugeloberfläche. Um in einer solchen Fläche eine physikalische Messung einer in der Fläche veränderlichen Größe durchführen zu können, muss man in jedem interessierenden Flächenpunkt eine Messanordnung wählen. Mögen also in den Flächenpunkten A und B zwei Messgeräte vorhanden sein. Es stellt sich dann die Frage, ob die Ergebnisse der beiden Messgeräte überhaupt miteinander vergleichbar sind. Der naive Standpunkt wäre zunächst die Annahme, dass die Messergebnisse schon vergleichbar sein werden, wenn nur der technische Aufbau der beiden Messgeräte vollkommen gleich ist.
Man kann diese Annahme aber leicht verwerfen, indem man sich in Erinnerung ruft, dass zum Beispiel die Vermessung geometrischer Größen von der Orientierung des Messgerätes abhängt. Wenn man sich vorstellt, die Messung bestünde darin, die Länge und Breite eines flachen Gegenstandes, etwa eines Blattes Papier zu bestimmen, dann ist unmittelbar einsichtig, dass das Messgerät unterschiedliche Werte liefert, je nachdem, wie es orientiert ist. Man könnte dagegen einwenden, dass man so verfahren kann, dass das Messgerät am vermessenen Gegenstand ausgerichtet wird und so immer normierte Werte liefert. Doch dann verliert man die Information darüber, wie zwei Gegenstände in den Punkten A und B relativ zueinander orientiert sind.
Selbst wenn man aber diese rein geometrischen Schwierigkeiten in der Messvorschrift ohne weiteres lösen könnte, dann müsste man immer noch in Zweifel ziehen, ob zwei identisch aufgebaute Messgeräte tatsächlich an zwei entfernten Punkten immer vergleichbare Messwerte liefern. Vielmehr besteht grundsätzlich immer die Möglichkeit, dass die Messgeräte noch gewisse innere Eigenschaften besitzen, die sich bei der Bewegung vom einen zum anderen Ort verändern. So kann zumindest zur Veranschaulichung dienen, dass ein Meterstab aus einem Kunststoff aufgrund seiner Wärmedehnung am Äquator andere Längenwerte liefert als an einem der Pole, zumal der vermessene Gegenstand in der Regel eine andere, unter Umständen geringere Wärmedehnung aufweist als der Meterstab.
Folgender Einwand ist nun aber der Ansatz zur Lösung der beschriebenen Problematik. Man könnte nämlich vorschlagen, statt zweier Messgeräte nur eines zu nehmen und dieses von A nach B zu transportieren. Man mag dann im zweiten Schritt auf die Idee kommen, dass dieser Transport so zu geschehen habe, dass das Messgerät in B einfach parallel zu seiner ehemaligen Orientierung im Punkt A steht. Man denkt dabei möglicherweise daran, wie einfach es ist, im dreidimensionalen euklidischen Anschauungsraum eine Parallelverschiebung eines Gegenstandes durchzuführen.
Es zeigt sich jedoch, dass es nicht immer am einfachsten ist, die Geometrie einer gekrümmten Fläche mit Hilfe des anschaulichen Parallelitätsbegriffs eines ungekrümmten Einbettungsraums zu beschreiben. Spätestens aber wenn ein solcher Einbettungsraum überhaupt nicht anschaulich und ohne weiteres verfügbar ist, gerät man mit dieser Vorgehensweise in methodische Schwierigkeiten, da dann nicht mehr unmittelbar klar ist, wie eine Parallelverschiebung durchzuführen ist. Ein solcher Fall liegt beispielsweise in der allgemeinen Relativitätstheorie vor.
Somit ist also gezeigt, dass die Vermessung physikalischer Objekte einer Vorschrift bedarf, wie das Messgerät von A nach B parallel zu verschieben ist. Die Beschreibung einer solchen Vorschrift wird sicherlich einfacher, wenn die Punkte A und B sehr nahe beieinander liegen und die Veränderung des Messgerätes dabei sehr klein ist. Man betrachtet daher mathematische Grenzübergänge, bei denen die Verschiebungen gegen Null gehen. Wenn man ferner einen solchen Paralleltransport eines Messgeräts beschrieben hat, kann man alternativ dazu natürlich auch den Paralleltransport von mit dem Messgerät ermittelten Größen beschreiben. Wenn sich das Messgerät also etwa relativ zum vermessenen Gegenstand nach links dreht, so dreht sich vereinfacht gesprochen der Gegenstand und die an ihm ermittelten Messgrößen relativ zum Messgerät nach rechts. Im folgenden soll ausschließlich die Veränderung der Messgrößen durch den Paralleltransport beschrieben werden.
Der mathematisch etablierte Name für den infinitesimalen Paralleltransport ist Zusammenhang oder auch Konnexion.
Mathematische Beschreibung
Im folgenden werden mehrere zu vermessende Größen zu einem Vektor in einer bestimmten Koordinatendarstellung zusammengefasst. Die einzelnen Größen seien dabei durch lateinische Indizes voneinander unterschieden, also etwa die Größe
 . Diese Messgrößen können, müssen aber nicht notwendigerweise Längen sein. Demgegenüber seien Koordinaten von Punkten des betrachteten Raumes mit griechischen Indizes bezeichnet, also etwa
. Diese Messgrößen können, müssen aber nicht notwendigerweise Längen sein. Demgegenüber seien Koordinaten von Punkten des betrachteten Raumes mit griechischen Indizes bezeichnet, also etwa  . Dabei habe der betrachtete Raum nicht notwendigerweise die Dimension zwei, wie oben durch das anschauliche Beispiel angedeutet. Ferner sei dieser Raum auch nicht zu verwechseln mit einem ungekrümmten Einbettungsraum.
. Dabei habe der betrachtete Raum nicht notwendigerweise die Dimension zwei, wie oben durch das anschauliche Beispiel angedeutet. Ferner sei dieser Raum auch nicht zu verwechseln mit einem ungekrümmten Einbettungsraum.Was man also letztendlich zu messen trachtet, ist ein Feld von Messgrößen
 für alle Punkte
für alle Punkte 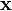 der Mannigfaltigkeit. Der endliche Paralleltransport der Messgrößen aufgrund der entsprechenden Veränderung des Messgerätes beim Transport von Punkt A nach Punkt B wird dann beschrieben durch
der Mannigfaltigkeit. Der endliche Paralleltransport der Messgrößen aufgrund der entsprechenden Veränderung des Messgerätes beim Transport von Punkt A nach Punkt B wird dann beschrieben durch
oder wenn man die Indizes unterdrückt, d.h. in Vektor-/Operatorschreibweise

Die Matrix der Größen
 stellt dabei eine lineare Abbildung dar, welche zusätzlich von den beteiligten Raumpunkten A und B abhängt. Dass es sich dabei um eine lineare Abbildung handeln muss, ist durchaus keine selbstverständliche Tatsache. Man könnte sich nämlich auch vorstellen, dass ein Messgerät auf nichtlineare Weise verzerrt wird. Demgegenüber werden aber Messgeräte möglichst immer so konstruiert, dass sie ihre Messwerte durch lineares „Vervielfältigen“ einer bestimmten Einheit gewinnen. So ist zum Beispiel ein Meterstab bildlich gesprochen nur eine Aneinanderreihung von gleichartigen Markierungen im Abstand eines „Urmillimeters“. Wenn in einem anderen Raumpunkt sich das „Urmillimeter“ verändert, dann wird man auch einen entsprechenden Meterstab wiederum linear durch Aneinandersetzen desselben konstruieren. Dennoch ist zu diskutieren, inwieweit das lineare Vervielfältigen überhaupt möglich ist, wenn große Krümmungen über die Ausdehnung des Messgerätes existieren.
stellt dabei eine lineare Abbildung dar, welche zusätzlich von den beteiligten Raumpunkten A und B abhängt. Dass es sich dabei um eine lineare Abbildung handeln muss, ist durchaus keine selbstverständliche Tatsache. Man könnte sich nämlich auch vorstellen, dass ein Messgerät auf nichtlineare Weise verzerrt wird. Demgegenüber werden aber Messgeräte möglichst immer so konstruiert, dass sie ihre Messwerte durch lineares „Vervielfältigen“ einer bestimmten Einheit gewinnen. So ist zum Beispiel ein Meterstab bildlich gesprochen nur eine Aneinanderreihung von gleichartigen Markierungen im Abstand eines „Urmillimeters“. Wenn in einem anderen Raumpunkt sich das „Urmillimeter“ verändert, dann wird man auch einen entsprechenden Meterstab wiederum linear durch Aneinandersetzen desselben konstruieren. Dennoch ist zu diskutieren, inwieweit das lineare Vervielfältigen überhaupt möglich ist, wenn große Krümmungen über die Ausdehnung des Messgerätes existieren.In diesem Sinne kann ein wohlgeformtes Messgerät für die praktische Anwendung der Differentialgeometrie nur ein solches sein, welches so klein ist, dass eine Krümmung des Raums und seiner Eigenschaften über seine Ausdehnung ohne Belang ist. Für ein solches Messgerät ist die Annahme eines linearen Paralleltransports gerechtfertigt. Im ähnlichen Sinne sind auch die Messvorschriften der Elektrodynamik mittels Probeteilchen zu verstehen, also Teilchen, die so klein sind, dass sich ihre dynamischen Eigenschaften nur aus einem Punkt, und nicht etwa eines ganzen Raumbereiches des äußeren Feldes ergeben.
Der obige Paralleltransport hat noch eine nichtlokale Form, da er von jeweils zwei Raumpunkten abhängt. Daher soll wie bereits oben angedeutet zu infinitesimal benachbarten Raumpunkten übergegangen werden. Es ergibt sich mit

 .
.Wenn nicht verschoben wird, findet natürlich definitionsgemäß auch kein Paralleltransport statt und daher ist
 die Identische Abbildung. Es ergibt sich also
die Identische Abbildung. Es ergibt sich also .
.Die kovariante Richtungsableitung wird nun wie gewohnt als Grenzübergang eines Differenzenquotienten zwischen den Punkten A und B geschrieben, hier jedoch nach der Anwendung des Paralleltransportes auf den Vektor im Punkt A zum Zwecke der Vergleichbarkeit:
 .
.Da die Richtung der Ableitung beliebig ist, ergibt sich also für die kovariante Ableitung schließlich

Das Feld
 stellt dabei den eigentlichen differentialgeometrischen Zusammenhang dar. Jedem Raumpunkt und jeder Raumkoordinatenrichtung μ wird dabei eine Matrix bzw. eine lineare Abbildung zugeordnet, welche angibt, wie sich Messwerte ändern, wenn sie zum Zwecke der messtechnischen Vergleichbarkeit zu in der genannten Richtung benachbarten Punkten paralleltransportiert werden.
stellt dabei den eigentlichen differentialgeometrischen Zusammenhang dar. Jedem Raumpunkt und jeder Raumkoordinatenrichtung μ wird dabei eine Matrix bzw. eine lineare Abbildung zugeordnet, welche angibt, wie sich Messwerte ändern, wenn sie zum Zwecke der messtechnischen Vergleichbarkeit zu in der genannten Richtung benachbarten Punkten paralleltransportiert werden.Anwendung in der Elektrodynamik
Die kovariante Ableitung in der Elektrodynamik stellt eine kompakte Schreibweise der vier Maxwellgleichungen (Wellengleichungen) in der vierdimensionalen Raumzeit dar.
Sie enthält das elektromagnetische 4er-Potenzial in der Raumzeit bzw. den daraus abgeleiteten elektromagnetischen Feldstärketensor und den 4er Strom. Die homogenen & inhomogenen Maxwellgleichungen lassen sich dann schreiben als:
Unter Verwendung der Lorenzeichung
 ergibt sich eine Gleichung (mit dem D’Alembertoperator
ergibt sich eine Gleichung (mit dem D’Alembertoperator  ):
):Anwendung in der Quantenelektrodynamik
Die kovariante Ableitung in der Quantenelektrodynamik enthält das elektromagnetische Vektorpotenzial. Die griechischen Indizes nehmen dabei die Werte 0 bis 3 oder seltener 1 bis 4, je nach Konvention, an. Einer der Indizes repräsentiert dabei die Zeitkoodinate, die anderen drei die Raumkoordinaten. Der Ausformulierung dieses Koordinatenformalismus widmet sich unter anderem die spezielle Relativitätstheorie.

worin Aμ wie gesagt für jedes μ eine reelle Zahl, insgesamt also ein raumzeitlicher Vektor ist. Das Auftreten dieser kovarianten Ableitung in den gekoppelten Feldgleichungen von Feld und Ladungsträgern sorgt letztendlich dafür, dass die quantenmechanische Wellenfunktion lokal eichinvariant ist, was wiederum in der heutigen Theorie der mathematische Grund für die Erhaltung der elektrischen Ladung ist. Letzteres kommt im Satz von Noether zum Ausdruck.
Die vierdimensionale Rotation des Vektorpotenzials ergibt die elektrischen bzw. magnetische Felder, d.h. den elektromagnetischen Feldtensor. Der elektromagnetische Feldtensor ist ein Sonderfall eines Riemannschen Krümmungstensors, bei dem der Zusammenhang ausschließlich von kommutierenden Matrizen gebildet wird, genauer gesagt sogar einfach von imaginären Zahlen. Die daraus folgenden endlichen Paralleltransporte stellen dann komplexe Zahlen vom Betrag eins dar und repräsentieren somit ebene Drehungen in einem abstrakten Raum.
Anwendung in der Yang-Mills-Theorie
Auch in den Yang-Mills-Theorien die zur Beschreibung der starken Wechselwirkung herangezogen wird, betrachtet man kovariante Ableitungen der oben angegebenen allgemeinen Form. Die lateinischen Indizes, also diejenigen Indizes, welche die Wirkung des Paralleltransports als linearer Abbildung der Messgrößen beschreiben, bezeichnen dabei Koordinaten im sogenannten Isospinraum. Dieser abstrakte Raum, welcher nicht offensichtlich mit dem physikalischen vierdimensionalen Raum zusammenhängt, repräsentiert die verschiedenen Typen von Elementarteilchen. Vereinfacht gesagt legt die Orientierung eines Teilchens im Isospinraum fest, um welche Art von Elementarteilchen es sich handelt.
Anders jedoch als beim einfachen Fall der Elektrodynamik sind im Isospinraum mehrere verschiedene Drehungen als Paralleltransport möglich. Schon im dreidimensionalen Anschauungsraum ergeben sich verschiedene Resultate, wenn man einen Körper um zwei unterschiedliche Achsen dreht, je nachdem in welcher Reihenfolge man die beiden Drehungen ausführt. Man sagt dann, die Drehungen kommutieren nicht, oder sie bildeten eine nichtabelsche/nichtkommutative Gruppe. Entsprechendes gilt daher auch für Drehungen im Isospinraum.
Die Nichtvertauschbarkeit von Drehungen hat tiefgreifende Auswirkungen auf die Theorie. Durch sie erhält der Krümmungstensor, also das Analogon zu den elektrischen und magnetischen Feldern der Elektrodynamik, eine Form, in der nicht nur einfache Ableitungen vorkommen, sondern auch Quadrate des Zusammenhangs, also des Vektorpotentials
 . Diese Nichtlinearität von nichtabelschen Eichtheorien führt dazu, dass die Yang-Mills-Felder mit sich selbst wechselwirken und zwei Wellen dieser Felder sich nicht mehr ungestört durchdringen.
. Diese Nichtlinearität von nichtabelschen Eichtheorien führt dazu, dass die Yang-Mills-Felder mit sich selbst wechselwirken und zwei Wellen dieser Felder sich nicht mehr ungestört durchdringen.Anwendung in der allgemeinen Relativitätstheorie
In der allgemeinen Relativitätstheorie werden als Messgrößen unmittelbar die Koordinatendarstellungen von Tangentenvektoren des Minkowskiraums verstanden, und nicht etwa von der Raumzeit unabhängige Größen wie in der Quantenfeldtheorie. Der Zusammenhang beschreibt also letztendlich, wie sich die eigentliche Geometrie der Messgeräte für Länge und Zeit beim Paralleltransport in der Raumzeit verändert.
Auf Grundlage dieser Vorstellung hat sich besonders eine auf Albert Einstein zurückgehende Veranschaulichung der gekrümmten Raumzeit mittels Dreibeinen von Meterstäben und Uhren als maßgeblichen Messgeräten etabliert.
Der Zusammenhang in der allgemeinen Relativitätstheorie wird daher durch einen Satz von linearen Abbildungen gegeben, welche auf der Raumzeit selbst wirken. Daher wird in diesem Zusammenhang auf den Gebrauch der weiter oben verwendeten lateinischen Indizes verzichtet. Die genauere Betrachtung zeigt, dass der Zusammenhang durch die Christoffelsymbole gegeben ist, welche sich auf eine bestimmte Weise aus dem metrischen Tensorfeld der Raumzeit berechnen:

Die kovariante Ableitung eines Vektorfeldes
 lautet also:
lautet also: .
.Hierbei wurde auf das Summationszeichen verzichtet im Sinne der Einsteinschen Summenkonvention.
Da jedes
 eine allgemeine Matrix darstellt, muss im allgemeinen davon ausgegangen werden, dass die verschiedenen
eine allgemeine Matrix darstellt, muss im allgemeinen davon ausgegangen werden, dass die verschiedenen  nicht miteinander vertauschen. Dies hat zur Folge, dass, ähnlich der Lage bei den Yang-Mills-Theorien, der Krümmungstensor in der allgemeinen Relativitätstheorie einen Anteil besitzt, welcher den Zusammenhang quadratisch enthält. Da aus dem Krümmungstensor in der allgemeinen Relativitätstheorie der Einstein-Tensor hervorgeht, welcher der eigentliche Feldtensor ist, ist es auch hier der Fall, dass selbst die quellenfreien Feldgleichungen nichtlinear sind und somit die Gravitationsfelder mit sich selbst wechselwirken. Sollten eines Tages einmal Gravitationswellen nachweisbar sein, und sollten sie der ART nachweislich gehorchen, so werden sie einander nicht ungestört durchdringen, wie das bei freien elektromagnetischen Wellen der Fall ist.
nicht miteinander vertauschen. Dies hat zur Folge, dass, ähnlich der Lage bei den Yang-Mills-Theorien, der Krümmungstensor in der allgemeinen Relativitätstheorie einen Anteil besitzt, welcher den Zusammenhang quadratisch enthält. Da aus dem Krümmungstensor in der allgemeinen Relativitätstheorie der Einstein-Tensor hervorgeht, welcher der eigentliche Feldtensor ist, ist es auch hier der Fall, dass selbst die quellenfreien Feldgleichungen nichtlinear sind und somit die Gravitationsfelder mit sich selbst wechselwirken. Sollten eines Tages einmal Gravitationswellen nachweisbar sein, und sollten sie der ART nachweislich gehorchen, so werden sie einander nicht ungestört durchdringen, wie das bei freien elektromagnetischen Wellen der Fall ist.Die Bahnen frei fallender Teilchen sind in der ART gegeben durch Geodäten, also die lokal kürzesten Wege zwischen zwei Raumzeitpunkten. Es zeigt sich, dass dies genau diejenigen Bahnen sind, deren Tangentenvektoren, das sind die Vektoren der relativistischen Vierergeschwindigkeit, eine verschwindende kovariante Ableitung in Richtung der Kurve besitzen. Da verschwindende kovariante Ableitung bedeutet, dass kein Unterschied besteht zwischen einem an einen bestimmten Ort transportierten Vektor und dem dort schon befindlichen Vektor, sagt man in diesem Fall, das Vektorfeld werde in dieser Richtung parallel transportiert. In Anwendung auf die Geodäten bedeutet das, dass der Tangentenvektor einer Geodäte sich selbst entlang der Bahnkurve parallel transportiert:
uμDμuκ = 0
und daher
 .
.Man stelle sich eine große Schar von frei fallenden Teilchen vor, im Idealfall in jedem Raumzeitpunkt eines. Diese definieren dann eine Schar von Geodäten. Die Tangentenvektoren an diese Geodäten definieren dann weiter ein Vektorfeld
 auf der Raumzeit. Sei nun
auf der Raumzeit. Sei nun  eine zugehörige Parametrisierung einer Geodäten mit einem entsprechenden Kurvenparameter τ, es gelte also
eine zugehörige Parametrisierung einer Geodäten mit einem entsprechenden Kurvenparameter τ, es gelte also  .
.Wenn man nun
 als Maß der Geschwindigkeit des Teilchens ansieht, dann kann diese Geschwindigkeit wiederum entlang der Geodäten abgeleitet werden, um dann durch Anwendung der Kettenregel der Differentiation die Beschleunigung zu erhalten:
als Maß der Geschwindigkeit des Teilchens ansieht, dann kann diese Geschwindigkeit wiederum entlang der Geodäten abgeleitet werden, um dann durch Anwendung der Kettenregel der Differentiation die Beschleunigung zu erhalten:
Da wie oben erwähnt die Tangentenvektoren der Geodäte entlang der Geodäte parallel transportiert werden, kann die partielle Ableitung des Geschwindigkeitsfeldes durch den Zusammenhang ausgedrückt werden:

Aus der Bedingung, dass das Tangentenfeld der Geodätenschar entlang seiner selbst parallel transportiert wird, folgt also schließlich die Geodätengleichung für eine einzelne Teilchenbahn:

Die Bedingung dafür, dass obiges
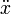 tatsächlich als Beschleunigung gedeutet werden kann, zumindest im nichtrelativistischen Grenzfall, ist, dass die Vierergeschwindigkeit, also die Tangente an die Bahnkurve auf das Quadrat der Lichtgeschwindigkeit normiert ist:
tatsächlich als Beschleunigung gedeutet werden kann, zumindest im nichtrelativistischen Grenzfall, ist, dass die Vierergeschwindigkeit, also die Tangente an die Bahnkurve auf das Quadrat der Lichtgeschwindigkeit normiert ist:uμuμ = c2
Der zugehörige Kurvenparameter, der dies ermöglicht, wird Eigenzeit τ genannt.
Wie bereits erwähnt wurde, bedeutet das Vorhandensein eines Zusammenhangs allein noch nicht das Vorliegen einer Krümmung. Vielmehr kann der Zusammenhang auch einfach daraus resultieren, dass man „irrtümlich“ ein falsches, weil krummliniges Koordinatensystem in einem flachen Raum gewählt hat. Insofern rechtfertigt sich auch nicht die Aussage, die Geodätengleichung lasse auf die Wirkung einer Raumkrümmung und damit der Gravitation schließen. Dieser Zusammenhang erschließt sich erst anhand der sogenannten Deviationsgleichung, welche den Krümmungstensor enthält. Wenn allerdings tatsächlich eine Krümmung vorliegt, dann beschreibt die Geodätengleichung unter anderem auch deren Effekte, neben den Effekten der Koordinatenwahl.
Im flachen Raum der speziellen Relativitätstheorie bei Wahl kartesischer Koordinaten verschwinden die Christoffelsymbole, und somit geht dann die kovariante Ableitung in die partielle Ableitung und die Geodätengleichung in die newtonsche Gleichung der Trägheitsbewegung über.
Literatur
- Michael Peskin und Daniel Schroeder: An Introduction to Quantum Field Theory. Perseus Books, Reading, Massachusetts, ISBN 0-201-50397-2
- Charles Misner, Kip Thorne und John Archibald Wheeler: Gravitation. W.H.Freeman & Co Ltd, ISBN 0-716-70344-0
Wikimedia Foundation.