- Konstruierbares Vieleck
-
In der Mathematik ist ein konstruierbares Polygon ein regelmäßiges Polygon, das mit Zirkel und (unmarkiertem) Lineal konstruiert werden kann. Zum Beispiel ist ein regelmäßiges Pentagon konstruierbar, ein regelmäßiges Heptagon hingegen nicht.
Inhaltsverzeichnis
Konstruierbarkeit
Um den Begriff „mit Zirkel und Lineal konstruierbar“ mathematisch präzise zu erfassen, muss definiert werden, was mit diesen Werkzeugen möglich ist. Wir gehen davon aus, dass am Anfang einer jeden Konstruktion zwei Punkte gegeben sind. Mit dem Lineal kann man dann eine Gerade durch zwei Punkte konstruieren, mit dem Zirkel einen Kreis mit einem Punkt als Mittelpunkt, der einen anderen Punkt berührt. Außerdem seien die Schnittpunkte von Geraden und Kreisen konstruierbar.
Aus diesen Grundkonstruktionen lassen sich eine Reihe weiterer Konstruktionen ableiten, wie die Konstruktion einer Mittelsenkrechte oder das Fällen eines Lotes. Man nennt dann eine Zahl konstruierbar, wenn man zwei Punkte konstruieren kann, so dass der euklidische Abstand zwischen diesen Punkte genau dem Betrag dieser Zahl entspricht (wobei der Abstand zweier vorgegebener Punkte als 1 definiert wird). Ist beispielsweise die Zahl a > 0 konstruierbar, so kann man mit Hilfe des Höhensatzes zwei Punkte mit Abstand
 konstruieren. Sind zwei Zahlen a und b konstruierbar, so mit Hilfe des Strahlensatz auch die Zahlen ab und
konstruieren. Sind zwei Zahlen a und b konstruierbar, so mit Hilfe des Strahlensatz auch die Zahlen ab und  bzw. durch Abgreifen eines Abstandes auch die Zahlen a + b und a - b. Ein Winkel α heiße konstruierbar, wenn die Zahl cosα konstruierbar ist; der Sinn dieser Definition erschließt sich schnell durch Betrachten des Einheitskreises.
bzw. durch Abgreifen eines Abstandes auch die Zahlen a + b und a - b. Ein Winkel α heiße konstruierbar, wenn die Zahl cosα konstruierbar ist; der Sinn dieser Definition erschließt sich schnell durch Betrachten des Einheitskreises.Um nun ein regelmäßiges n-Eck zu konstruieren, genügt es, den Zentriwinkel
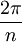 zu konstruieren, denn wenn man den Mittelpunkt des n-Ecks und eine Ecke gegeben hat, lässt sich ausgehen von der Verbindungsgeraden durch Mittelpunkt und Eckpunkt der nächste Eckpunkt konstruieren. Ist umgekehrt ein regelmäßiges n-Eck gegeben, so kann man den Zentriwinkel abgreifen. Zur Lösung der Frage, ob das n-Eck konstruierbar ist, ist man also auf den Fall zurückgeführt, zu entscheiden, ob der Zentriwinkel konstruierbar ist.
zu konstruieren, denn wenn man den Mittelpunkt des n-Ecks und eine Ecke gegeben hat, lässt sich ausgehen von der Verbindungsgeraden durch Mittelpunkt und Eckpunkt der nächste Eckpunkt konstruieren. Ist umgekehrt ein regelmäßiges n-Eck gegeben, so kann man den Zentriwinkel abgreifen. Zur Lösung der Frage, ob das n-Eck konstruierbar ist, ist man also auf den Fall zurückgeführt, zu entscheiden, ob der Zentriwinkel konstruierbar ist.Kriterium für Konstruierbarkeit
Carl Friedrich Gauß zeigte 1796, dass das regelmäßige Siebzehneck konstruierbar ist, indem er den algebraischen Ausdruck für
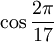 explizit angab. Durch die in seinen Disquisitiones arithmeticae entwickelte Theorie gelang es Gauß fünf Jahre später, eine hinreichende Bedingung für die Konstruktion regelmäßiger Polygone anzugeben:
explizit angab. Durch die in seinen Disquisitiones arithmeticae entwickelte Theorie gelang es Gauß fünf Jahre später, eine hinreichende Bedingung für die Konstruktion regelmäßiger Polygone anzugeben:- Wenn n ein Produkt einer Potenz von 2 und paarweise voneinander verschiedenen Fermatschen Primzahlen ist, dann ist das regelmäßige n-Eck konstruierbar.
Gauß wusste zwar, dass die Bedingung auch notwendig ist, hat allerdings seinen Beweis hierfür nicht veröffentlicht. Pierre-Laurent Wantzel holte dies 1837 nach.
Man kann zeigen, dass eine Zahl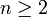 genau dann ein Produkt einer Potenz von 2 und verschiedenen Fermatschen Primzahlen ist, wenn
genau dann ein Produkt einer Potenz von 2 und verschiedenen Fermatschen Primzahlen ist, wenn 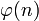 eine Potenz von 2 ist. Hierbei bezeichnet
eine Potenz von 2 ist. Hierbei bezeichnet  die Eulersche φ-Funktion.
die Eulersche φ-Funktion.Zusammenfassend sind also für eine Zahl
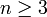 äquivalent:
äquivalent:- Das regelmäßige n-Eck ist mit Zirkel und Lineal konstruierbar.
 für
für 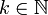 und
und  verschiedene fermatsche Primzahlen.
verschiedene fermatsche Primzahlen. für
für  .
.
Sind insbesondere m und n teilerfremd und sowohl das m-Eck als auch das n-Eck konstruierbar, so ist wegen
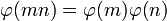 auch das mn-Eck konstruierbar. Für diese Tatsache lässt sich auch direkt die geometrische Konstruktion angeben, denn wenn m und n teilerfremd sind, so gibt es mit dem Lemma von Bézout zwei ganze Zahlen a und b mit 1 = am + bn. Indem man nun a-mal den Zentriwinkel des n-Ecks und b-mal den Zentriwinkel des m-Ecks anlegt, hat man den Winkel
auch das mn-Eck konstruierbar. Für diese Tatsache lässt sich auch direkt die geometrische Konstruktion angeben, denn wenn m und n teilerfremd sind, so gibt es mit dem Lemma von Bézout zwei ganze Zahlen a und b mit 1 = am + bn. Indem man nun a-mal den Zentriwinkel des n-Ecks und b-mal den Zentriwinkel des m-Ecks anlegt, hat man den Winkel  konstruiert, und somit das mn-Eck.
konstruiert, und somit das mn-Eck.
In folgender Tabelle sind die konstruierbaren n-Ecke für aufgeführt, markiert durch Fettdruck in der ersten Zeile:
aufgeführt, markiert durch Fettdruck in der ersten Zeile:-
n 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 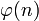
2 2 4 2 6 4 6 4 10 4 12 6 8 8 16 6 18 8 12 10 22 8 20 12 18 12 28 8 30 16 20 16
Die konstruierbaren Polygone sind Folge A003401 in OEIS, die nicht konstruierbaren sind Folge A004169 in OEIS.
Insbesondere sieht man, dass die allgemeine Dreiteilung des Winkels nicht möglich ist, denn das regelmäßige Dreieck ist konstruierbar während das regelmäßige Neuneck nicht konstruierbar ist. Mit anderen Worten, der Winkel von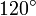 kann nicht mit Zirkel und Lineal dreigeteilt werden.
kann nicht mit Zirkel und Lineal dreigeteilt werden.Galoistheorie
Durch Entwicklung der Galoistheorie gelangte man zu einer tieferen Einsicht in das Problem. Die Menge der konstruierbaren Zahlen bildet nämlich einen Körper, in dem zusätzlich auch aus positiven Zahlen die Quadratwurzel gezogen werden kann. Insbesondere entspricht das Schneiden von Geraden dem Lösen einer linearen Gleichung und das Schneiden einer Geraden mit einem Kreis oder das Schneiden zweier Kreise dem Lösen einer quadratischen Gleichung. In der Sprache der Körpererweiterungen ist das folgende Tatsache:
- Ist a eine konstruierbare Zahl, so gibt es einen Körperturm
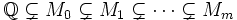 , so dass
, so dass 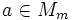 und
und ![M_{i+1}=M_i[\sqrt{\gamma_i}]](/pictures/dewiki/100/da4fdf729243e55343e4149d64bc421e.png) für ein
für ein 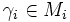 .
.
Umgekehrt ist natürlich auch jede Zahl aus Mm konstruierbar. Ist also a konstruierbar, so ist a algebraisch und es ist
![[\mathbb{Q}[a]:\mathbb{Q}]=2^m](/pictures/dewiki/55/779f07f60a3e5c5e3cd7555bef2b890b.png) eine Potenz von 2.
eine Potenz von 2.
Zur Klärung der Konstruktion von regelmäßigen n-Ecken mit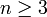 betrachtet man Kreisteilungskörper
betrachtet man Kreisteilungskörper ![\mathbb{Q}[\zeta_n]](/pictures/dewiki/99/ce1178d78e079a24b8a39a38f26e1e26.png) als Körpererweiterung über
als Körpererweiterung über 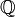 , wobei
, wobei 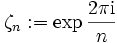 die n-te Einheitswurzel bezeichnet. Die n-ten Einheitswurzeln sind die auf dem Einheitskreis liegenden Ecken eines regelmäßigen n-Ecks. Es genügt die reelle Zahl
die n-te Einheitswurzel bezeichnet. Die n-ten Einheitswurzeln sind die auf dem Einheitskreis liegenden Ecken eines regelmäßigen n-Ecks. Es genügt die reelle Zahl 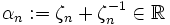 zu konstruieren.
zu konstruieren.Sind zum Beispiel m und n teilerfremd, so ist
![\mathbb{Q}[\zeta_{mn}]=\mathbb{Q}[\zeta_m,\zeta_n]](/pictures/dewiki/51/3956bb5b30fe0bfe729a8cf80689b063.png) . Sind dann das m- und das n-Eck konstruierbar, so ist auch das mn-Eck konstruierbar.
. Sind dann das m- und das n-Eck konstruierbar, so ist auch das mn-Eck konstruierbar.Um nun obige Argumente anwenden zu können, müssen eine Körpererweiterungsgrade bestimmt werden. Da die Kreisteilungspolynome irreduzibel sind, ist
![[\mathbb{Q}[\zeta_n]:\mathbb{Q}] = \varphi(n)](/pictures/dewiki/50/2bc010c8aca3f78b375f7c34fa3ca16e.png) . Wegen
. Wegen 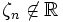 ist
ist ![[\mathbb{Q}[\zeta_n]:\mathbb{Q}[\alpha_n]]>1](/pictures/dewiki/57/960cb9db5be688ebc6bc08e2dcd6176e.png) , also ist
, also ist ![\operatorname{MinPol}_{\mathbb{Q}[\alpha_n]}(\zeta_n) = X^2-\alpha_nX+1](/pictures/dewiki/49/1f6013696a9971d67f05421f70f49b8a.png) , und damit
, und damit ![[\mathbb{Q}[\zeta_n]:\mathbb{Q}[\alpha_n]]=2](/pictures/dewiki/97/a1080e95683621d70e4fd570c2508436.png) .
.
Im regelmäßigen n-Eck beträgt der Zentriwinkel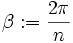 . Ist somit das regelmäßige n-Eck konstruierbar, so auch eine Strecke der Länge
. Ist somit das regelmäßige n-Eck konstruierbar, so auch eine Strecke der Länge  . Wegen
. Wegen 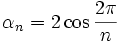 ist dann auch diese Zahl konstruierbar, also muss
ist dann auch diese Zahl konstruierbar, also muss ![[\mathbb{Q}[\alpha_n] : \mathbb{Q}] = 2^m](/pictures/dewiki/52/45d58b81899daa8ecf3af2cf7b7ba081.png) eine Potenz von zwei sein. Damit ist dann
eine Potenz von zwei sein. Damit ist dann ![\varphi(n) = [\mathbb{Q}[\zeta_n]:\mathbb{Q}] = [\mathbb{Q}[\zeta_n]:\mathbb{Q}[\alpha_n]]\cdot[\mathbb{Q}[\alpha_n]:\mathbb{Q}] = 2^{m+1}](/pictures/dewiki/49/1e96b2fdd9d8ef4f6aaa8a6da7d8c09d.png) .
.
Ist umgekehrt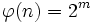 , so ist
, so ist ![\operatorname{Gal}(\mathbb{Q}[\zeta_n]:\mathbb{Q})\cong\left(\Z/n\Z\right)^\times](/pictures/dewiki/50/295c202b0a75e03043156d43882e7f29.png) eine endliche abelsche Gruppe der Ordnung 2m. Mit dem Hauptsatz über endlich erzeugte abelsche Gruppen existiert dann eine Kette von sukzessiven Normalteilern
eine endliche abelsche Gruppe der Ordnung 2m. Mit dem Hauptsatz über endlich erzeugte abelsche Gruppen existiert dann eine Kette von sukzessiven Normalteilern 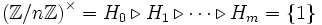 mit | Hi | = 2m − i. Mit dem Hauptsatz der Galoistheorie erhält man daraus dann als Fixkörper von
mit | Hi | = 2m − i. Mit dem Hauptsatz der Galoistheorie erhält man daraus dann als Fixkörper von ![\mathbb{Q}[\zeta_n]](/pictures/dewiki/99/ce1178d78e079a24b8a39a38f26e1e26.png) einen Körperturm
einen Körperturm ![\mathbb{Q}=M_0\subseteq M_1\subseteq\dots\subseteq M_m=\mathbb{Q}[\zeta_n]](/pictures/dewiki/51/332011c320bbf9b8a2a73a7220454920.png) mit [Mi + 1:Mi] = | Hi / Hi + 1 | = 2, mithin ist
mit [Mi + 1:Mi] = | Hi / Hi + 1 | = 2, mithin ist ![M_{i+1}=M_i[\sqrt{\gamma_i}]](/pictures/dewiki/100/da4fdf729243e55343e4149d64bc421e.png) für
für 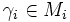 , und somit ist ζn und damit auch das regelmäßige n-Eck konstruierbar.
, und somit ist ζn und damit auch das regelmäßige n-Eck konstruierbar.
Sei beispielsweise n = 5. Dann ist eine Potenz von 2 und
eine Potenz von 2 und ![\operatorname{Gal}(\mathbb{Q}[\zeta_5]:\mathbb{Q})\cong\left(\Z/5\Z\right)^\times = \langle2\rangle](/pictures/dewiki/99/ccdedbf44b351d011449302ffb858d79.png) , da 2 eine Primitivwurzel modulo 5 ist. Eine mögliche Kette von Normalteilern ist
, da 2 eine Primitivwurzel modulo 5 ist. Eine mögliche Kette von Normalteilern ist 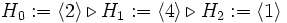 . Der dazugehörige Körperturm ist
. Der dazugehörige Körperturm ist ![M_0:=\mathbb{Q} \subseteq M_1:=\mathbb{Q}[\zeta_5+\zeta_5^{-1}] \subseteq M_2:=\mathbb{Q}[\zeta_5]](/pictures/dewiki/99/ceef313938fd3917d9418dbdc4bb59a2.png) . Es ist
. Es ist 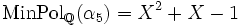 , da es normiert ist und α5 annulliert und mit Reduktion modulo 2 irreduzibel ist. Nach Lösen der Gleichung x2 + x − 1 = 0 ergibt sich
, da es normiert ist und α5 annulliert und mit Reduktion modulo 2 irreduzibel ist. Nach Lösen der Gleichung x2 + x − 1 = 0 ergibt sich 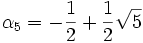 . Nun könnte man bereits die erste Ecke konstruieren, indem man den Punkt mit Abstand α5 vom Mittelpunkt auf einer Achse aus konstruiert und dann das Lot durch diesen Punkt fällt. Durch Lösen von x2 − α5x + 1 = 0 ergibt sich
. Nun könnte man bereits die erste Ecke konstruieren, indem man den Punkt mit Abstand α5 vom Mittelpunkt auf einer Achse aus konstruiert und dann das Lot durch diesen Punkt fällt. Durch Lösen von x2 − α5x + 1 = 0 ergibt sich  . Durch diesen algebraischen Ausdruck lässt sich alternativ die erste Ecke konstruieren, indem man eine reelle und eine imaginäre Achse einzeichnet und mit deren Hilfe den Punkt ζ5 konstruiert.
. Durch diesen algebraischen Ausdruck lässt sich alternativ die erste Ecke konstruieren, indem man eine reelle und eine imaginäre Achse einzeichnet und mit deren Hilfe den Punkt ζ5 konstruiert.Weblinks
- Eric W. Weisstein: Constructible Polygon auf MathWorld (englisch)
Wikimedia Foundation.
