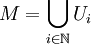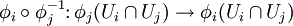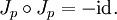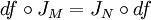- Komplexe Geometrie
-
Komplexe Mannigfaltigkeiten sind topologische Mannigfaltigkeiten, deren Kartenwechselhomöomorphismen sogar konform sind. Diese Objekte werden in der Differentialgeometrie und der Funktionentheorie untersucht. Ihre Definition ist analog zu der Definition der differenzierbaren Mannigfaltigkeit, jedoch kann im Gegensatz zu den differenzierbaren Mannigfaltigkeiten nicht jede komplexe Mannigfaltigkeit in den
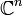 eingebettet werden.
eingebettet werden.Inhaltsverzeichnis
Definition
Sei M ein topologischer Hausdorff-Raum, welcher dem zweiten Abzählbarkeitsaxiom genügt.
Eine Karte ist eine offene Teilmenge
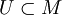 zusammen mit einem Homöomorphismus
zusammen mit einem Homöomorphismus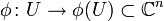 .
.
Eine Karte ist also ein 2-Tupel (U,φ).
Ein komplexer Atlas ist eine Menge solcher Karten, so dass
gilt, mit der Eigenschaft, dass für je zwei Karten (Ui,φi) und (Uj,φj) die Kartenwechselabbildungen
konform (biholomorph) sind.
Eine komplexe Mannigfaltigkeit' ist ein topologischer Hausdorff-Raum, welcher dem zweiten Abzählbarkeitsaxiom genügt und einen Atlas besitzt. Man sagt M hat Dimension n, wenn die Kartenwechselhomöomorphismen in den
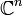 abbilden.
abbilden.Eigenschaften
- Komplexe Mannigfaltigkeiten der Dimension 1 werden als Riemann'sche Flächen bezeichnet. Diese darf man nicht mit den Riemann'schen Mannigfaltigkeiten verwechseln.
- Jede komplexe Mannigfaltigkeit der Dimension n, kann auch als glatte Mannigfaltigkeit der Dimension 2n aufgefasst werden.
- Jede komplexe Mannigfaltigkeit ist orientierbar.
- Der Raum der holomorphen Funktion
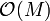 von M nach
von M nach 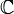 enthält, falls M kompakt ist, nur die konstanten Funktion. Deshalb interessiert man sich dafür, ob eine komplexe Mannigfaltigkeit holomorph separabel ist.
enthält, falls M kompakt ist, nur die konstanten Funktion. Deshalb interessiert man sich dafür, ob eine komplexe Mannigfaltigkeit holomorph separabel ist.
- Kompakte, komplexe Mannigfaltigkeiten können nicht in den
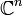 eingebettet werden.
eingebettet werden.
Beispiele
- Der Vektorraum
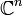 und offene Teilmenge davon.
und offene Teilmenge davon. - Allgemeine Stein'sche Mannigfaltigkeiten
- Komplex-projektive Räume
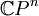
- Riemannsche Flächen wie zum Beispiel die riemannsche Zahlenkugel, die Jacobi-Varietät und die punktierte komplexe Ebene.
- Kählermannigfaltigkeiten
Fastkomplexe Mannigfaltigkeiten
Eine Abschwächung des Begriffs komplexe Mannigfaltigkeit ist der Begriff der fastkomplexen Mannigfaltigkeit. Während komplexe Mannigfaltigkeiten lokal wie der komplexe Raum aussehen, tun dies fastkomplexe nur „infinitesimal“, d. h. die Tangentialräume sind (auf untereinander verträgliche Art) komplexe Vektorräume. Um einen reellen Vektorraum zu einem komplexen zu machen, muss man festlegen, was das Produkt eines Vektors mit der imaginären Einheit i sein soll. Dies ist im Fall des Tangentialraums TpM die Aufgabe der Abbildung Jp.
Eine fastkomplexe Struktur auf einer glatten Mannigfaltigkeit M ist eine glatte Abbildung
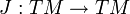 mit der Eigenschaft, dass die Einschränkung
mit der Eigenschaft, dass die Einschränkung 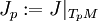 auf den Tangentialraum zu jedem Punkt
auf den Tangentialraum zu jedem Punkt 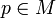 eine bijektive lineare Abbildung ist, die
eine bijektive lineare Abbildung ist, dieerfüllt. (Dies entspricht der Gleichheit i2 = − 1)
Eine fastkomplexe Mannigfaltigkeit ist eine glatte Mannigfaltigkeit M zusammen mit einer fastkomplexen Struktur auf M.
Seien M und N zwei fastkomplexe Mannigfaltigkeiten mit den jeweiligen fastkomplexen Strukturen JM und JN. Eine stetig differenzierbare Abbildung
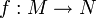 heißt holomorph (oder pseudo-holomorph), wenn der Push-Forward
heißt holomorph (oder pseudo-holomorph), wenn der Push-Forward 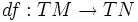 von f mit den fastkomplexen Strukturen von M und N verträglich ist, das heißt
von f mit den fastkomplexen Strukturen von M und N verträglich ist, das heißtgilt.
Eine komplexe Mannigfaltigkeit ist automatisch auch eine fastkomplexe. Durch die komplexe Struktur werden die Tangentialräume zu komplexen Vektorräumen und durch Jv: = iv für
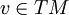 wird eine fastkomplexe Struktur definiert. Umgekehrt braucht eine fastkomplexe Mannigfaltigkeit im allgemeinen keine komplexe Struktur zu besitzen. Falls es aber einen Atlas gibt mit Karten, deren Zielbereich ein komplexer Vektorraum ist und die im Sinne der fastkomplexen Struktur holomorph sind, dann ist dieser Atlas ein komplexer Atlas, der die fastkomplexe Struktur induziert. Man kann deshalb komplexe Mannigfaltigkeiten auch definieren als fastkomplexe Mannigfaltigkeiten, die einen holomorphen Atlas besitzen.
wird eine fastkomplexe Struktur definiert. Umgekehrt braucht eine fastkomplexe Mannigfaltigkeit im allgemeinen keine komplexe Struktur zu besitzen. Falls es aber einen Atlas gibt mit Karten, deren Zielbereich ein komplexer Vektorraum ist und die im Sinne der fastkomplexen Struktur holomorph sind, dann ist dieser Atlas ein komplexer Atlas, der die fastkomplexe Struktur induziert. Man kann deshalb komplexe Mannigfaltigkeiten auch definieren als fastkomplexe Mannigfaltigkeiten, die einen holomorphen Atlas besitzen.Riemannsche Fläche
Im reell zweidimensionalen (d.h. im komplex eindimensionalen) ist jede fastkomplexe Mannigfaltigkeit eine komplexe Mannigfaltigkeit, also eine riemannsche Fläche, was man durch das Lösen der Beltrami-Gleichung zeigen kann.
Literatur
- Klaus Fritzsche & Hans Grauert - From Holomorphic Functions to Complex Manifolds, Springer-Verlag, ISBN 0-387-95395-7
Wikimedia Foundation.