- Kochkurve
-
Die Koch-Kurve oder kochsche Kurve ist ein von dem schwedischen Mathematiker Helge von Koch 1904 vorgestelltes Beispiel für eine überall stetige, aber nirgends differenzierbare Kurve. Es handelt sich bei ihr ferner um eines der ersten formal beschriebenen fraktalen Objekte. Die Koch-Kurve ist eins der am häufigsten zitierten Beispiele für ein Fraktal und wurde bei der Entdeckung als Monsterkurve bezeichnet. Die Koch-Kurve ist auch in Form der kochschen Schneeflocke bekannt, die durch geeignete Kombination dreier Koch-Kurven entsteht.
Inhaltsverzeichnis
Konstruktion
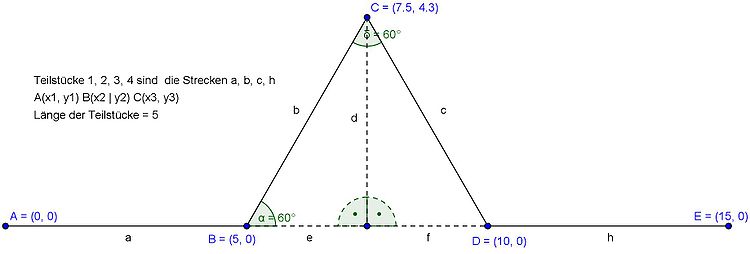
Man kann die Kurve anschaulich mittels eines iterativen Prozesses konstruieren (s. Lindenmayer-System). Zu Beginn besteht die Kurve aus einem einzigen Streckenstück. Die Iteration besteht nun darin, dass dieser Streckenabschnitt durch einen anderen, aus vier gleichlangen Strecken bestehenden Streckenabschnitt ersetzt wird, der wie folgt aufgebaut ist: Strecke – 60°-Winkel – Strecke – 120°-Winkel (in der Gegenrichtung) – Strecke – 60°-Winkel – Strecke. Jeder der vier neuen Streckenabschnitte hat 1/3 der Länge des ursprünglichen Streckenabschnitts. Im nächsten Schritt wird jeder der vier Streckenabschnitte durch einen Streckenabschnitt der oberen Art ersetzt. Und so weiter.
Diese Iteration wird nun beliebig oft wiederholt, wobei die Dreiecke stets zur selben Seite der Kurve hin zu errichten sind. Auf diese Weise ergibt sich eine Folge von Streckenzügen, die gegen die Koch-Kurve strebt.
Graphische Darstellung der Konstruktion
Die ersten drei Iterationen der Konstruktion
Nach fünf Iterationen:Dieses Konstruktionsprinzip, bei dem iterativ jede Teilstrecke durch einen Streckenzug ersetzt wird, lässt sich auch für die Erzeugung anderer fraktaler Kurven verwenden. So wird es beispielsweise bei der Drachenkurve eingesetzt.
Das Konstruktionsprinzip ist eng verwandt mit dem der Erzeugung der Cantor-Menge, welche man erhält, wenn man das mittlere Drittel der Strecke nicht ersetzt, sondern entfernt.
Definition des Grenzwerts
Der Grenzwert dieser Iteration (z. B. als IFS-Fraktal), die eigentliche Koch-Kurve, ist in gewissem Sinne unendlich fein strukturiert und kann daher nur näherungsweise graphisch dargestellt werden. In diesem Fall lässt sich der Grenzwert einfach wie folgt definieren:
- Zum Grenzwert der Iteration gehören diejenigen Punkte, die von irgendeinem Iterationsschritt an in allen folgenden Iterationen enthalten sind, sowie alle Häufungspunkte der so gebildeten Punktmenge.
Der linke Endpunkt des anfänglichen Streckenstücks ist beispielsweise in jeder Iteration enthalten und gehört damit zur Kochkurve. Der Mittelpunkt des anfänglichen Streckenstücks hingegen ist schon ab der ersten Iteration nicht mehr enthalten. Eine andere (gleichbedeutende) Grenzwertdefinition ist weiter unten durch die Parameterdarstellung f gegeben.
Eigenschaften
Eigenschaften aus der fraktalen Geometrie
Die Koch-Kurve ist nach ihrer Konstruktionsvorschrift streng selbstähnlich, das heißt, es erscheinen bei beliebiger Vergrößerung immer wieder die gleichen Strukturen.
Sie hat eine Hausdorff-Dimension von
Länge und Flächeninhalt
Die Länge der Kurve ist unbegrenzt, da der Streckenzug bei jedem Iterationsschritt um den Faktor 4/3 länger wird. Nach dem n-ten Iterationsschritt ist die Kurvenlänge also auf das (4 / 3)n-fache angewachsen.
Die (oben grün eingefärbte) Fläche „unterhalb“ der Kurve ist hingegen begrenzt. Wenn das Dreieck unterhalb der ersten Iteration den Flächeninhalt 1 hat, kommt bei der zweiten Iteration an jeder der 4 Strecken ein Dreieck mit Flächeninhalt 1/9 hinzu, und bei der n-ten Iteration kommt ein Flächeninhalt von
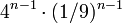 hinzu. Der gesamte Flächeninhalt berechnet sich demnach als geometrische Reihe zu
hinzu. Der gesamte Flächeninhalt berechnet sich demnach als geometrische Reihe zu-
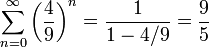 .
.
Stetigkeit und Differenzierbarkeit
Die Kurve ist überall stetig, aber nirgends differenzierbar. Zur Untersuchung dieser Eigenschaften betrachtet man die Parameterdarstellung
![f_n\colon [0,1]\to {\mathbb R}^2](/pictures/dewiki/56/8000ce895cf7b268864e93afe0958f8a.png) der n-ten Iteration und deren Grenzfunktion
der n-ten Iteration und deren Grenzfunktion 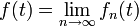 . Wenn man
. Wenn man ![t\in [0,1]](/pictures/dewiki/100/d9a06fde4663cdd5b1ba693e9127232f.png) als Zeitpunkt auffasst, ist fn(t) derjenige Punkt auf dem Streckenzug nach der n-ten Iteration, den man zum Zeitpunkt t erreicht, wenn man den Streckenzug mit konstanter Geschwindigkeit (allerdings mit 4n − 1 − 1 abrupten Richtungsänderungen) vom linken zum rechten Endpunkt durchläuft. Die Funktionen fn sind alle stetig und konvergieren gleichmäßig gegen die Grenzfunktion f, die nach einem Satz der Analysis darum ebenfalls stetig ist.
als Zeitpunkt auffasst, ist fn(t) derjenige Punkt auf dem Streckenzug nach der n-ten Iteration, den man zum Zeitpunkt t erreicht, wenn man den Streckenzug mit konstanter Geschwindigkeit (allerdings mit 4n − 1 − 1 abrupten Richtungsänderungen) vom linken zum rechten Endpunkt durchläuft. Die Funktionen fn sind alle stetig und konvergieren gleichmäßig gegen die Grenzfunktion f, die nach einem Satz der Analysis darum ebenfalls stetig ist.Kochsche Schneeflocke
Beginnt man den Ersetzungsprozess der Koch-Kurve nicht mit einer Strecke, sondern mit einem gleichseitigen Dreieck, dann erhält man die kochsche Schneeflocke. Sie besteht aus drei Koch-Kurven und schließt trotz ihrer unendlichen Länge nur einen Bereich mit endlicher Fläche ein.
Anwendung
- Ein Beispiel ist die Fraktalantenne
Erstveröffentlichungen
- Helge von Koch, Une courbe continue sans tangente, obtenue par une construction géometrique élémentaire. Arkiv för Matematik 1 (1904) 681-704.
- Helge von Koch, Une méthode géométrique élémentaire pour l'étude de certaines questions de la théorie des courbes planes. Acta Mathematica 30 (1906) 145-174.
Weblinks
Wikimedia Foundation.

.jpg)