Knotentheorie

Projektion des Kleeblattknotens

Die Knotentheorie ist ein Forschungsgebiet der Topologie. Sie beschäftigt sich unter anderem damit, die topologischen Eigenschaften von Knoten zu untersuchen. Eine Fragestellung ist etwa, ob zwei gegebene Knoten äquivalent sind, also ob sie ineinander überführt werden können, ohne dass dabei die Schnur „zerschnitten“ wird. Die Knotentheorie beschäftigt sich im Gegensatz zur Knotenkunde nicht mit dem Knüpfen von Knoten in der Praxis, sondern mit mathematischen Gebilden.

Mathematische Definition

Im mathematischen Sinn ist ein Knoten eine Einbettung einer Kreislinie in den dreidimensionalen Raum. Zwei Knoten gelten als gleich, wenn sie durch eine stetige Verformung ineinander überführt werden können (Isotopie).

In der Knotentheorie werden auch Einbettungen von mehreren Kreislinien untersucht; diese nennt man Verschlingungen. Eine andere Erweiterung des Themas sind mehrdimensionale Knoten, das heißt Einbettungen der Sphären der Dimension n in den n+2-dimensionalen Raum für n>1.

Knotendiagramme und Reidemeister-Bewegungen

Ein wilder Knoten

In der Knotentheorie wird ein Knoten oft durch seine Projektion auf eine Ebene dargestellt. Die Projektion wird dabei so gewählt, dass sie nur endlich viele Doppelpunkte (Kreuzungen) hat. Knoten, bei denen man eine solche Projektion nicht angeben kann, bezeichnet man als wilde Knoten, diejenigen mit einer solchen Projektion als zahme Knoten. Zum Beispiel ist jeder stückweise glatte Knoten zahm. In der Knotentheorie werden hauptsächlich Eigenschaften von zahmen Knoten untersucht.

Um aus einer Projektion den Knoten rekonstruieren zu können, muss man bei jeder Kreuzung angeben, welcher der beiden Stränge oben bzw. unten liegt. Eine Projektion mit dieser Zusatzinformation nennt man ein Knotendiagramm. Jeder zahme Knoten lässt sich somit durch ein Diagramm darstellen. Ein solches Diagramm ist jedoch nicht eindeutig, denn jeder Knoten lässt sich durch unendlich viele verschiedene Diagramme darstellen. Zum Beispiel ändern die folgenden lokalen Züge zwar das Diagramm, nicht aber den dargestellten Knoten:

Die drei Bewegungstypen ( "Reidemeister-Bewegungen" )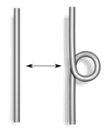

;	;	.
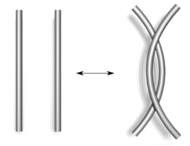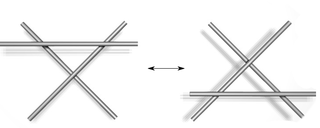Typ I	Typ II	Typ III

Diese Züge werden Reidemeister-Bewegungen genannt, zu Ehren von Kurt Reidemeister. Dieser hat 1927 gezeigt, dass diese drei Züge bereits ausreichen: Zwei Knotendiagramme stellen genau dann den gleichen Knoten dar, wenn sie durch eine endliche Folge von Reidemeister-Bewegungen ineinander überführt werden können.

Knoteninvarianten

Ein Ziel der Knotentheorie ist es, Knoten-Invarianten zu finden, also mathematische Objekte, die sich nicht ändern, wenn man den Knoten im dreidimensionalen Raum stetig deformiert. Einige Beispiele von Knoteninvarianten sind Polynome, z. B. das Jones-Polynom, das HOMFLY-Polynom oder das Kauffman-Polynom. Diese Polynome kann man mit Hilfe von Knotendiagrammen algorithmisch berechnen, indem man für alle Kreuzungen geeignete Terme zu einem Gesamtpolynom addiert. Zur Invarianz genügt es zu zeigen, dass das so konstruierte Polynom invariant unter den drei Reidemeister-Bewegungen ist.

Bis heute ist noch keine einfach berechenbare Knoten-Invariante gefunden worden, die alle nicht-äquivalenten Knoten unterscheidet, welche also die Eigenschaft hat, dass die Invariante für zwei Knoten genau dann identisch ist, wenn die zwei Knoten äquivalent sind. Dies ist ein wichtiges Ziel der aktuellen Forschung (Lösungen hierfür gibt es eventuell im Bereich der Floer-Homologien). Es ist auch unbekannt, ob das Jones-Polynom den trivialen Knoten erkennt, also ob es einen nicht-trivialen Knoten gibt, dessen Jones-Polynom gleich dem des trivialen Knoten ist.

Anwendungen

Lange Zeit war die Beschäftigung mit Knoten eher eine brotlose Kunst. Mittlerweile existieren aber eine Reihe wichtiger Anwendungen, etwa in der Biochemie bzw. Strukturbiologie, mit denen überprüft werden kann, ob komplizierte Faltungen von Proteinen mit anderen Proteinen übereinstimmen. Ähnliches gilt für die DNA. Weitere aktuelle Anwendungen gibt es in der Polymerphysik. Eine wichtige Stellung nimmt die Knotentheorie in der modernen theoretischen Physik ein, wo es etwa um Pfade in Feynmandiagrammen geht.

Die Knotentheorie wird auch in benachbarten Gebieten der Topologie und Geometrie genutzt. Zur Untersuchung 3-dimensionaler Räume sind Knoten sehr nützlich, da sich jede orientierbare geschlossene 3-dimensionale Mannigfaltigkeit durch Dehn-Chirurgie an einem Knoten oder einer Verschlingung erzeugen lässt. In der hyperbolischen Geometrie spielen Knoten eine Rolle, weil die Komplemente der meisten Knoten in der 3-dimensionalen Sphäre S³ eine vollständige hyperbolische Metrik tragen.

Siehe auch

• Borromäische Ringe
• Zopfgruppe

Literatur

• Colin C. Adams: The Knot Book. An elementary introduction to the mathematical theory of knots. 1994; 2004, ISBN 0-8218-3678-1
  • Das Knotenbuch. Einführung in die mathematische Theorie der Knoten. Spektrum, Heidelberg/Berlin/Oxford 1995, ISBN 3-86025-338-7
• Meike Akveld: Knoten in der Mathematik. Ein Spiel mit Schnüren, Bildern und Formeln. Orell Fuessli, Zürich 2007, ISBN 978-3-280-04050-8
• Gerhard Burde & Heiner Zieschang: Knots. de Gruyter, Berlin/New York 1985, ISBN 3-11-008675-1
• Gunnar Hornig: Magnetes Geheimnis. In: RUBIN – Das Wissenschaftsmagazin der Ruhr-Universität Bochum. 2/01, S. 6–10 (PDF)
• Louis H. Kauffman: Knots and Physics. World Scientific, 1991, ISBN 981-02-0343-8
  • Knoten. Diagramme, Zustandsmodelle, Polynominvarianten. Spektrum, Heidelberg/Berlin/Oxford 1995, ISBN 3-86025-232-1
• Lee Neuwirth: Theorie der Knoten. In: Spektrum der Wissenschaft. August 1979, ISSN 0170-2971 (unter anderem: Modell eines mathematischen Knotens, Beziehungen zwischen Geometrie und Algebra)
• Dale Rolfsen: Knots and Links. AMS Chelsea Publ., 2003, ISBN 0-8218-3436-3
• Alexei Sossinsky: Nœuds. Genèse d'une théorie mathématique. Éditions du Seuil, Paris 1999, ISBN 2-02-032089-4 (Science Ouverte).
  • Mathematik der Knoten. Rowohlt-Taschenbuch-Verlag, Reinbek 2000, ISBN 3-499-60930-4

Weblinks

• The KnotPlot Site von Robert G. Scharein (Software für interaktives Visualisieren, Manipulieren und Simulieren von mathematischen Knoten)