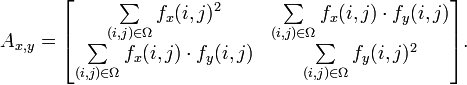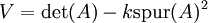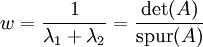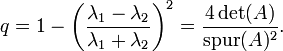Interest-operator

Bild mit markanten Punkten (rote Kreuze). Benutzt wurde der Harris Corner Detector

Mit Interest-Operatoren werden auf dem Bereich der Bildverarbeitung Algorithmen bezeichnet, die markante Stellen in Bildern extrahieren und gleichzeitig eine oder mehrere Kenngrößen liefern.

Einleitung

Markante Stellen in Bildern sind diejenigen Punkte, die in einer begrenzten Umgebung möglichst einzigartig sind. An die Interest-Operatoren werden folglich verschiedene Anforderungen gestellt:

1. Die detektierten Punkte sollen deutlich, das heißt lokal einzigartig und vom Hintergrund unterscheidbar sein. Auch ihre Seltenheit, das heißt ihre Unterscheidbarkeit zu anderen Bildpunkten, soll möglichst groß sein.
2. Invarianz gegenüber Bildänderungen wie geometrischen und radiometrischen Verzerrungen
3. Unempfindlichkeit gegenüber Rauschen.

Das Ergebnis der Suche nach markanten Punkten wird zum Beispiel bei der Berechnung der Epipolargeometrie zwischen zwei Kameras oder beim bildbasierten Tracking verwendet.

Einzelne Operatoren

Bekannte Interest-Operatoren sind der Moravec-Operator, der Plessy Punkt-Detektor und der Förstner-Operator.

Moravec-Operator

Der Moravec-Operator wurde von Hans Moravec im Jahr 1977 vorgestellt. ^[1] Er berechnet die mittleren quadratischen Gradientensummen in den vier Hauptrichtungen des Fensters der Größe 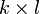$k \times l$. Linienhafte Kanten werden somit nicht als markant markiert.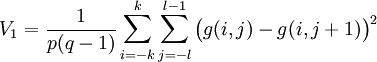

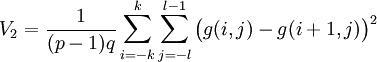
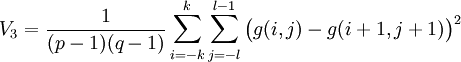
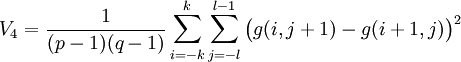
$V_1=\frac{1}{p(q-1)}\sum_{i=-k}^k\sum_{j=-l}^{l-1}\bigl(g(i,j)-g(i,j+1)\bigr)^2$

$V_2=\frac{1}{(p-1)q}\sum_{i=-k}^k\sum_{j=-l}^{l-1}\bigl(g(i,j)-g(i+1,j)\bigr)^2$

$V_3=\frac{1}{(p-1)(q-1)}\sum_{i=-k}^k\sum_{j=-l}^{l-1}\bigl(g(i,j)-g(i+1,j+1)\bigr)^2$

$V_4=\frac{1}{(p-1)(q-1)}\sum_{i=-k}^k\sum_{j=-l}^{l-1}\bigl(g(i,j+1)-g(i+1,j)\bigr)^2$

V = min(V₁,V₂,V₃,V₄)

mit p = 2k + 1 und q = 2l + 1.

Liegt der Wert über einer bestimmten Schwelle, liegt ein markanter Punkt vor. Der Moravec-Operator ist sehr leicht zu implementieren und benötigt wenig Rechenzeit. Er ist aber nicht rotationsinvariant und seine Genauigkeit beträgt lediglich 1 Pixel.

Plessy Punkt-Detektor

Der Plessy Punkt-Detektor (auch Harris Corner Detector genannt) wurde 1988 von Harris und Stephens vorgestellt. ^[2] Sie beschrieben eine Verbesserung des Moravec-Operators, indem sie die diskreten Verschiebungen und Richtungen mit Hilfe der Autokorrelationsfunktion lösten und damit auch die Genauigkeit der Lokalisierung steigerten.

Die Autokorrelationsmatrix A berechnet sich dabei durch Summierung der Ableitung der Bildfunktion f in dem Gebiet Ω um einen Punkt:

$A_{x,y}= \begin{bmatrix} \sum\limits_{(i,j)\in\Omega}f_x(i,j)^2 & \sum\limits_{(i,j)\in\Omega}f_x(i,j)\cdot f_y(i,j) \\ \sum\limits_{(i,j)\in\Omega}f_x(i,j)\cdot f_y(i,j) & \sum\limits_{(i,j)\in\Omega}f_y(i,j)^2 \\ \end{bmatrix}.$

f_x und f_y sind dabei die partiellen Ableitungen der Bildfunktion f.

A beschreibt die Nachbarschaftsstruktur um die Stelle (x,y). Ihr Rang unterscheidet sich je nach Eigenschaft der Umgebung:

Rang 2: Es liegt ein markanter Punkt vor.

Rang 1: Es liegt eine gerade Kante vor.

Rang 0: Es liegt eine homogene, unstrukturierte Fläche vor.

Die Punktstärke V wird aus A mittels der Formel

$V=\det(A)-k\operatorname{spur}(A)^2$

ermittelt. Um eine Trennung der Kanten von markanten Punkten zu erhalten, wird k = 0,04 gewählt. Auf diese Weise erhält man für Punkte positive und für Kanten negative Werte. Eine lokale Nicht-Maxima-Unterdrückung liefert schließlich die Position des Interest-Punktes.

Förstner-Operator

Der Förstner-Operator ^[3] bestimmt markante Punkte auch mittels der Autokorrelationsmatrix A. Hierbei wird ausgenutzt, dass die Matrix A ^{− 1} der Kovarianzmatrix entspricht, also angibt, wie genau die Position des Interestpunkts bestimmt werden kann (große Gradienten in A führen zu kleinen Varianzen bzw. Kovarianzen in A ^{− 1} und damit zu genauer Bestimmbarkeit). Die Achsen und Achsabschnitte der entsprechenden Fehlerellipse korrespondieren mit den Eigenvektoren und Eigenwerten λ₁,λ₂ der Matrix A ^{− 1}.

Ein guter Interestpunkt liegt vor, wenn die Fehlerellipse möglichst klein und möglichst rund ist. Im Gegensatz dazu besitzt die Fehlerellipse entlang einer ausgeprägten Grauwertkante eine sehr kleine und eine sehr große Halbachse (λ₁ klein, λ₂ groß), der Punkt wäre also senkrecht zur Kante gut, entlang der Kante jedoch schlecht bestimmt.

Die Größe und Rundheit wird anhand der folgenden beiden Maßzahlen beurteilt, der Größe

$w=\frac 1{\lambda_1+\lambda_2}=\frac{\det(A)}{\operatorname{spur}(A)}$

und der Rundheit

$q=1-\left(\frac{\lambda_1-\lambda_2}{\lambda_1+\lambda_2}\right)^2=\frac{4\det(A)}{\operatorname{spur}(A)^2}.$

Zu beachten ist, dass λ₁,λ₂ die Eigenwerte von A ^{− 1} (nicht von A) sind. Durch die gegebenen Formeln lassen sich jedoch w und q ohne Inversion bzw. Eigenwertzerlegung berechnen.

Anhand dieser beiden Kenngrößen kann die Eignung eines Interestpunkts beurteilt werden:

1. Markante Punkte besitzen kleine, kreisförmige Ellipsen.
2. Gerade Kanten lassen sich durch langgestreckte Fehlerellipsen detektieren.
3. Große Ellipsen kennzeichnen eine unstrukturierte, gleichförmige Fläche.

Als Faustregel für einen Interestpunkt kann man q > 0,8 angeben. Für w ist die Angabe schwieriger, da sie vom Bildkontrast abhängig ist. Eine Methode besteht darin, x Prozent der Punkte mit den größten Werten auszuwählen, also z. B. von allen Punkten (welche die Bedingung an q erfüllen) die 10 % mit größtem w. Alternativ kann man sich aus dem Mittelwert aller w über das gesamte Bild einen Schwellwert berechnen. Der Wert von w ist zugleich die „Stärke“ des Interestpunkts.

Die subpixelgenaue Berechnung des Interestpunktes wurde von Förstner ebenfalls beschrieben. das heißt, obwohl die Bewertung einer Umgebung anhand der Maße w und q nur auf Pixelgrenzen erfolgt, kann ein (Eck- oder Zentrums-) Punkt subpixelgenau berechnet werden.

Referenzen

1. ↑ H. P. Moravec: Towards Automatic Visual Obstacle Avoidance. In: Proceedings of the 5th International Joint Conference on Artificial Intelligence. 1977, S. 584. 
2. ↑ C. Harris and M. Stephens: A combined corner and edge detector. In: Proceedings of the 4th Alvey Vision Conference. 1988, S. 17-151. 
3. ↑ W. Förstner und E. Gülch: A Fast Operator for Detection and Precise Location of Distinct Points, Corners and Centers of Circular Features. In: Proceedings of the ISPRS Intercommission Workshop on Fast Processing of Photogrammetric Data. 1987, S. 281-305.