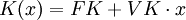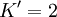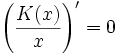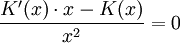- Grenzaufwand
-
Die Grenzkosten (auch Marginalkosten) sind in der Betriebswirtschaftslehre und der Mikroökonomik die Kosten, die durch die Produktion einer zusätzlichen Einheit eines Produktes entstehen. Mathematisch ist die Grenzkostenfunktion die erste Ableitung (die Steigung) der Kostenfunktion. Historisch ist die Grenzkostenbetrachtung auf das Marginalprinzip zurückzuführen.
Inhaltsverzeichnis
Beispiel
Für die Produktion eines Produktes X fallen Fixkosten in Höhe von 100.000 Euro an. Beispielsweise in Form von Mieten für Produktionsstätten, Kosten der Bereitstellung von Maschinen und Löhne für Mitarbeiter. Mit diesen vorhandenen Mitteln können maximal 5000 Einheiten eines Produktes gefertigt werden. Für die Fertigung einer Einheit von X werden Rohstoffe für 5 Euro benötigt (variable Kosten).
Bei einer gefertigten Einheit fallen also Gesamtkosten der Produktion in Höhe von 100.005 Euro, für zwei gefertigte Einheiten 100.010 Euro usw. an. Mit jeder produzierten Einheit erhöhen sich die Gesamtkosten um 5 Euro – dieser Betrag entspricht den Grenzkosten.
Angenommen der Lieferant für die Rohstoffe gewährt einen Mengennachlass (Rabatt) in Höhe von 0,50 Euro ab 3000 Einheiten Rohstoff und 1 Euro für eine Abnahme ab 4000 Einheiten. Bis zu einer Produktion von 2999 Einheiten betragen die Grenzkosten dann 5 Euro, zwischen 3000 und 3999 Einheiten betragen die Grenzkosten 4,50 Euro und ab 4000 Einheiten 4 Euro – die Grenzkosten fallen also.
Steigt die Nachfrage auf über 5000 Stück, wird also die Kapazitätsgrenze der Produktion überschritten, so werden weitere Kosten für die Ausweitung der Produktion benötigt. Beispielsweise müssen höhere (variable) Kosten für die Wartung von Maschinen und Überstundenzuschüsse für das Personal kalkuliert werden. An diesem Punkt steigen die Grenzkosten.
Alternative Definitionen
- „Grenzkosten sind der Kostenzuwachs, der durch die Mehrproduktion einer Ausbringungseinheit entsteht. “
Abzugrenzen ist hierbei jedoch der Begriff der sogenannten sprungfixen Kosten. Diese entstehen beim Überschreiten einer Kapazitätsstufe zusätzlich zu den absolut fixen Kosten der jeweils vorherigen Kapazitätsstufe und fallen in der neuen Kapazitätsstufe unabhängig vom Beschäftigungsgrad an. Folglich bedeutet dies für die angegebene Grenzkostendefinition, dass sie nur genau solange ihre Richtigkeit behält, wie die zusätzliche Produktionseinheit innerhalb einer Kapazitätsstufe erstellt werden kann. Voraussetzung hierfür ist, dass in der Kapazitätsstufe, in der sich eine Unternehmung momentan befindet (z. B. vorhandene Maschinen, Anlagen, Produktionshallen), noch freie Kapazitäten vorhanden sind. Ist diese Voraussetzung nicht erfüllt, so müssen zwangsläufig sprungfixe Kosten anfallen, da für die Produktion einer zusätzlichen Leistungseinheit neue Kapazitäten geschaffen werden müssen in Form von Investitionen.
- „Grafisch betrachtet sind die Grenzkosten die Steigung der Tangente der Gesamtkostenkurve für die untersuchte Ausbringungsmenge.“[1]
Auch diese Definition deckt nur einen Teil der notwendigen Erläuterungsbestandteile der Grenzkosten ab. Sprungfixe Kosten spielen bei Grenzkosten, wie bereits oben erläutert, stets eine wichtige Rolle und sollten deshalb nicht außer Acht gelassen werden. Weiterhin ist auch der Fixkostenblock jeder Unternehmung in die Diskussion einzubeziehen, um den Schnittpunkt der Kostenfunktion mit der Ordinate zu ermitteln und sich den Verlauf der Kosten- als auch der Grenzkostenfunktion vorstellen zu können. Vor allem durch technische Standards entstehen in Unternehmen vermehrt Fixkostenbestandteile, die besonders bei mittel- und langfristigen Entscheidungen in den Mittelpunkt rücken müssen.
Grenzkostenfunktion
Die Grenzkostenfunktion stellt grafisch die erste Ableitung der Kostenfunktion dar. Diese wird im Folgenden, angewandt auf zwei verschiedene Funktionstypen, näher erläutert. Auf der Abszisse wird dabei die Ausbringungsmenge x (Output) abgetragen und auf der Ordinate die dazugehörigen Gesamtkosten K.
Linearer Kostenverlauf
Um zunächst das Prinzip der Grenzkosten darzustellen, wird der lineare Kostenverlauf anhand eines Beispiels erläutert, auch wenn dieser in der Praxis so gut wie nie in reiner Form vorkommt. Die Gesamtkosten ergeben sich aus der Summe von fixen Kosten FK und variablen Kosten VK, wobei letztere mit der Ausbringungsmenge x multipliziert werden.
Die Grafik 1 stellt eine lineare Kostenfunktion dar mit der allgemeinen Form
In dem Beispiel lautet die Kostenfunktion K(x) = 2x + 1, d. h. die Fixkosten betragen eins (z. B. Geldeinheiten: €) und die sich mit der Ausbringungsmenge ändernden variable Kosten entsprechen zwei. Diese bildet den orangen Graph mit einem Schnittpunkt mit der y- Achse im Punkt (0;1) und einem positiven Anstieg von zwei ab. Um die Grenzkosten zu ermitteln, muss man die mathematische Definition der Grenzkosten praktisch umsetzen und die Kostenfunktion K nach x differenzieren. Somit ergibt sich als erste Ableitung K':
Die Grenzkostenfunktion (grün dargestellt) verhält sich unabhängig von der Ausbringungsmenge x und verläuft als Gerade parallel zur Abszisse. Dieser lineare Kostenverlauf stellt einen Sonderfall der Grenzkosten dar, da die Grenzkosten GK gleich den variablen Kosten VK sind. Steigt die Produktion in diesem Unternehmen um eine Leistungseinheit, so steigen die Kosten um zwei Geldeinheiten unter den Voraussetzungen, die in Abschnitt 1 erläutert wurden.
Nicht-linearer Kostenverlauf
Der nicht-lineare Kostenverlauf beruht auf der ertragsgesetzlichen Kostenfunktion und hat bei weitem mehr praktische Relevanz als der lineare Kostenverlauf, da er die betrieblich anfallenden Kosten realistischer darstellt.
Die Grafik 2 veranschaulicht im oberen Abschnitt den Verlauf der Kostenfunktion K, die wie zu erkennen ist, nicht linear ist, d. h. nicht als Gerade interpretiert werden kann. Im unteren Abschnitt werden die sich aus der Kostenfunktion ergebenden durchschnittlichen variablen Kosten VDK (blauer Graph), durchschnittlichen gesamten Kosten TDK (gelber Graph) und die Grenzkosten GK (rosa Graph), die im Folgenden weiter analysiert werden, als eigenständige Funktionen dargestellt.
Im Betrieb geht man meist von sinkenden Grenzkosten aus, da sich die Herstellung von großen Mengeneinheiten für ein Unternehmen mehr rentiert als die Produktion von kleinen Mengen. Gründe hierfür sind Skalenerträge und Lernkurveneffekte. Der erste Abschnitt der Grenzkostenkurve bis zum Minimum der GK-Funktion verläuft daher zunächst fallend, d. h. mit steigender Ausbringungsmenge sinkt der Preis der jeweils zusätzlich produzierten Leistungseinheit. Hier sind die Grenzkosten kleiner als die durchschnittlichen gesamten Kosten TDK und die Skalenerträge nehmen zu. Es ist also möglich, den doppelten Output zu erreichen ohne dafür die doppelten Kosten zu verursachen. Dann erreicht die Grenzkostenfunktion ihr Minimum im Wendepunkt der Kostenfunktion K und die Grenzkosten steigen wieder an, die Grenzkosten sind jetzt größer als die durchschnittlichen gesamten Kosten TDK und die Skalenerträge nehmen ab, d.h. mit doppeltem Kosteneinsatz kann nicht der doppelte Absatz erreicht werden. Ursachen für diesen Verlauf sind mit Hilfe der ertragsgesetzlichen Kosten- bzw. Produktionsfunktion nachzuvollziehen. Die Grenzkostenfunktion schneidet die Durchschnittskostenfunktionen in deren Minimum.
Grenzkosten und Durchschnittskosten
Die Grenzkosten schneiden die Durchschnittskosten immer in deren Minimum. Dies hängt damit zusammen, dass die Tangente an die Kostenfunktion und die Gerade aus dem Ursprung, die ebenfalls an die Kostenfunktion angelegt wird, die gleiche Steigung haben. Damit sind die Durchschnittskosten
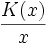 in diesem Punkt genauso hoch wie die Grenzkosten
in diesem Punkt genauso hoch wie die Grenzkosten 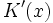 . Bei fallenden Grenzkosten liegt der Schnittpunkt beider Kurven im Maximum der Durchschnittskosten.
. Bei fallenden Grenzkosten liegt der Schnittpunkt beider Kurven im Maximum der Durchschnittskosten.Will man das Minimum der Durchschnittskosten ermitteln, so muss man die erste Ableitung der Durchschnittskostenfunktion gleich null setzen (
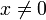 ) :
) :Daraus folgt nach der Quotientenregel:
Daraus folgt:
Das entspricht mathematisch wiederum dem Schnittpunkt der Grenzkosten K' mit den Durchschnittkosten
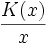 .
.Grundzüge der Gewinnmaximierung in kurzer Frist
Der Sektor der Unternehmen in ökonomischer Sicht hat immer das Ziel seine Gewinne zu maximieren, d. h. allen Unternehmen wird unterstellt, sie seien Gewinnmaximierer. Der Gewinn ergibt sich aus der Differenz von Gesamterlösen und den Gesamtkosten.
- Gewinn G = Gesamterlöse R - Gesamtkosten K
„Zur Gewinnmaximierung wählt ein Unternehmen den Output, bei dem die Differenz zwischen dem Erlös und den Kosten am größten ist.“ [2] Um dieses Ziel zu erreichen, muss ein Unternehmer vor allem bei seiner Kosten- und der damit verbundenen Preiskalkulation in Abhängigkeit seiner Marktform gut unterrichtet sein.
Gewinnmaximierung im Wettbewerbsunternehmen
Es wird die Marktform eines Polypols unterstellt, d. h. es herrscht vollkommene Konkurrenz zwischen den Unternehmen. Alle Wettbewerbsunternehmen sind der Nachfrage anderer Wirtschaftssektoren und auch des eigenen gleichermaßen ausgesetzt und somit gilt der Preis für ein Produkt als fix und der erzielbare Erlös aus einer zusätzlichen verkauften Leistungseinheit Grenzerlös R´entspricht dem Preis P, den ein Wirtschaftssubjekt für das Produkt zu zahlen hat. Es gilt für alle Wettbewerbsunternehmen die kurzfristige Gewinnmaximierungsbedingung:
- Grenzkosten K´ = Grenzerlös R´ = Preis P
Da der Preis als konstant angesehen wird, kann ein Polypolist die Gewinnmaximierung nur über die Absatzmenge regeln und nicht über den Preis.
Gewinnmaximierung im Monopol
Anders als der Polypolist kann der Monopolist aufgrund seiner starken Marktposition als einziger Käufer/Verkäufer seinen Gewinn auch über den Preis bestimmen. Er bestimmt den Schnittpunkt zwischen der Grenzerlöskurve und der Grenzkostenkurve und erhält dabei eine gewinnmaximierende Absatzmenge. Anhand der Nachfragefunktion kann der Monopolist den dazugehörigen Preis festlegen. Produziert der Monopolist unter der errechneten gewinnmaximierenden Menge, so hat er zwar weniger Kosten, aber die entgehenden Erlöse aus den zusätzlichen Verkäufen sind größer als die Kosten und führen somit zur Gewinnminderung. Stellt der Monopolist im Gegensatz dazu mehr als die gewinnmaximierende Produktionsmenge her, so entstehen ihm einerseits höhere Erlöse, andererseits übersteigen die Kosten für die zusätzliche Produktion über der Gleichgewichtsmenge die Erlöse und führen ebenfalls zur Gewinnschrumpfung. Es gilt die Gewinnmaximierungsbedingung:
- Grenzkosten K´ = Grenzerlös R´
Bei einem normalen Monopol gibt es einen Bereich, wo die Grenzkosten den fallenden Grenzerlös (Grenzumsatz) schneiden (Die Umsatzkurve ist bei linearer Nachfragekurve [P-Q] durch doppelte Fallrate aber gleichen Ausgangspunkt wie bei der Nachfragekurve gekennzeichnet.). In diesem Schnittpunkt (cournotscher Punkt) liegt für den Monopolisten die Kombination von angebotener Menge und erzieltem Preis, die den Gesamterlös maximiert. Dieser Preis wird, ceteris paribus, höher sein als beim Mengenanpasser, und die angebotene Menge geringer als bei der perfekten Konkurrenz.
Bei einem natürlichen Monopol nehmen die Durchschnittkosten mit der Menge immer weiter ab. Es gibt dann keinen Schnittpunkt zwischen Grenzkosten und Durchschnittskosten, da die Grenzkosten immer unterhalb der Durchschnittskosten liegen. Darum kann ein solcher natürlicher Monopolist seine Kosten nicht mit den Grenzkosten decken, sondern muss mindestens zu Durchschnittskosten anbieten. Erst wenn die Grenzkosten über den Durchschnittskosten liegen, kann der Preis gleich den Grenzkosten gesetzt werden, bei Deckung aller Kosten.
Wenn die Grenzkosten über den Durchschnittskosten ohne Fixkosten liegen, ist das Betriebsminimum erreicht. Der Betrieb sollte hierbei den nächstfolgenden Auftrag annehmen. Wenn er jedoch unter diese Grenze kommt, lohnt es nicht weiterzuproduzieren, da nicht einmal die variablen Kosten gedeckt werden können.
Besser ist es jedoch, wenn die Grenzkosten über den Durchschnittkosten inkl. Fixkosten liegen. Man bewegt sich bei dieser Produktionsmenge über dem Betriebsoptimum.
Formel:
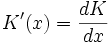 Die erste Ableitung der Kostenfunktion nach x.
Die erste Ableitung der Kostenfunktion nach x.Siehe auch
Einzelnachweise
- ↑ Vgl.:Rechnungswesen und Controlling; Bausteine des Rechnungswesens und ihre Verknüpfungen; Verlag neue Wirtschaftsbriefe(NWB),Herne/Berlin; 1998; S. 272, ISBN 3-482-48121-0
- ↑ Pindyck, Robert S.,Rubinfeld, Daniel L., Mikroökonomie, 6. Auflage, München, S. 361, ISBN 3-8273-7164-3
Literatur
- Rechnungswesen und Controlling; Bausteine des Rechnungswesens und ihre Verknüpfungen; Verlag neue Wirtschaftsbriefe, (NWB),Herne/Berlin; 1998; S. 272, ISBN 3-482-48121-0
- Robert S. Pindyck, Daniel L. Rubinfeld, Mikroökonomie, 6. Auflage, München, S. 361, ISBN 3-8273-7164-3
- Adolf E. Luger, Allgemeine Betriebswirtschaftslehre,Band 1: Der Aufbau des Betriebes, 5. Auflage,Carl Hanser Verlag, München Wien, ISBN 3-446-22539-0
Weblinks
Wikimedia Foundation.