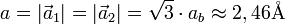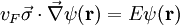- Graphene
-
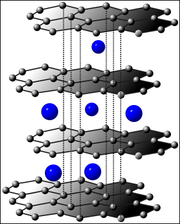
Graphen ([gʁa'feːn], engl. graphene) ist die Bezeichnung für einen zweidimensionalen hexagonalen Kristall aus sp2-gebundenen Kohlenstoff-Atomen. Diese monoatomare Kohlenstoffschicht wurde zum ersten Mal verwendet, um den Aufbau und die elektronischen Eigenschaften komplexerer Materialien aus Kohlenstoff beschreiben zu können. Durch Stapeln der Schichten erhält man das dreidimensionale Graphit[1], durch Aufrollen die eindimensionalen Kohlenstoffnanoröhren[2] und durch Einfügen von Fünfecken und anschließendes Zusammenballen erhält man die quasi-nulldimensionalen Fullerene[3].
Da solche strikt zweidimensionalen Strukturen wie Graphen thermodynamisch nicht stabil sein können[4][5], war es umso erstaunlicher als Novoselov et al.[6] 2004 die Präparation von freistehenden Graphenkristallen bekannt gab. Diese experimentellen Ergebnisse könnten durch die Existenz eines metastabilen Zustandes[7] oder durch Faltenbildung des Graphens[8] erklärt werden.
Wie bei Alkenen oder Benzen verweist die Endung -en des Namens auf ungesättigte Doppelbindungen in den Kohlenstoffringen.
Inhaltsverzeichnis
Struktur
Die Kohlenstoffatome sind in einer hexagonalen Honigwaben-Struktur angeordnet. Diese Anordnung resultiert aus der Hybridisierung („Verschmelzung“) der 2s-, 2px- und 2py-Orbitale der beteiligten Kohlenstoffatome zu sogenannten sp2-Hybridorbitalen, welche plane σ-Bindungen zu drei weiteren C-Atomen ausbilden. Die Honigwaben-Struktur ergibt sich aus den Bindungswinkeln β von β = 120°. Der Bindungsabstand ab der Kohlenstoffatome beträgt im Graphen ab=1,42 Å [9] Die übriggebliebenen 2px-Orbitale stehen senkrecht zur Graphenebene und bilden ein delokalisiertes π-Bindungssystem aus.[10]
Graphen besteht zudem aus zwei äquivalenten Untergittern A und B, denen die Kohlenstoffatome zugeordnet sind. Die Untergitter sind um die Bindungslänge ab gegeneinander verschoben. Die zweiatomige Einheitszelle wird durch zwei Gittervektoren
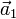 und
und 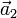 aufgespannt. Die Gittervektoren zeigen dabei auf die jeweils übernächsten Nachbarn. Die Länge der Vektoren und damit die Gitterkonstante a lässt sich berechnen zu
aufgespannt. Die Gittervektoren zeigen dabei auf die jeweils übernächsten Nachbarn. Die Länge der Vektoren und damit die Gitterkonstante a lässt sich berechnen zuHerstellung von Graphen
Mechanisch
Die ersten Graphenflakes wurden von Novoselov [6] durch Exfoliation von HOPG (eng. Highly Oriented Pyrolytic Graphite) erhalten. Dabei wurde Klebeband (wegen der Marktführerschaft in den USA oft Scotch-Tape genannt) auf das HOPG gedrückt und anschließend abgezogen, dabei bleibt Graphit im Klebstoff zurück. Danach wird der Klebstreifen auf einen Silicium-Wafer mit einer dünnen Siliciumdioxidschicht gedrückt und wieder abgezogen. Danach wird der Wafer mit einem optischen Mikroskop nach Graphenstücken abgesucht, dabei muss man bedenken, dass Graphitfilme dünner als 50 nm optisch transparent sind, was mit abnehmender Schichtdicke noch weiter zunimmt (vgl. lambert-beersches Gesetz). Diese dünnen 50-nm-Schichten sind, aus der Vielzahl der zurückgelassenen Graphitstücke, mit einem optischen Mikroskop nur durch Interferenzeffekte zu finden, das heißt, durch die zusätzliche Schicht verändern sich die Reflexionseigenschaften des Substrates, so dass sich die durch Interferenzeffekte verursachte violette Farbe der Siliciumdioxidschicht nach blau verändert. An den Rändern dieser 50-nm-Schichten kann man dann mit dem Rastertunnel- oder Rasterkraftmikroskop nach dünnerem Graphen suchen.
Bei einer weiteren Exfoliationsmethode werden vor dem Exfolitionsprozess mit einem Sauerstoffplasma Vertiefungen (im englischen als mesa bezeichnet) in das HOPG geätzt. Danach wird ein mit Klebstoff benetzter Glasträger mit auf die Oberfläche gedrückt und abgezogen. Die im Kleber haftenden Mesas werden nun ebenfalls solange mit Klebestreifen abgezogen, bis nur noch ein Rest übrig bleibt. Danach wird der Kleber in Aceton aufgelöst und die im Aceton gelösten Graphenflakes mit einem Siliciumwafer herausgefischt und wiederum mit optischem Mikroskop und Rastertunnel- oder Rasterkraftmikroskop abgesucht.
Bei diesen beiden Methoden handelt es sich um sehr zeitaufwändige Verfahren, bei denen man zwar hochwertige, aber nur sehr wenige Proben erhält.
Chemisch
Neben der mechanischen Exfoliation gibt es noch die Synthese aus organischen Molekülen[11] [12] und die chemische Exfoliation[13] bei der Graphit in organischen Lösungsmitteln in seine Basalebenen aufgespalten wird.
Am 11. November 2008 gab das California Nanosystems Institute (CNSI) bekannt, dass es Y. Yang gelungen sei, ein „Massenproduktionsverfahren“ für die Graphen-Synthese zu erarbeiten. Bei diesem neuen Verfahren wird Graphit-Oxid in flüssiges Hydrazin getaucht. Dem Forschungsteam ist es bereits gelungen eine Graphen-Monolage der Größe 40 µm × 20 µm zu erzeugen. Unter Fachleuten wird dieses Verfahren als sehr vielversprechend bezeichnet.
Epitaktisches Wachstum
Graphen kann epitaktisch auf metallischen Substraten wachsen. Eine in der Literatur vorgestellte Methode ist die Zersetzung von Ethen auf Iridium[14]. In einem weiteren Verfahren wird die Löslichkeit von Kohlenstoff in Übergangsmetallen verwendet[15]. Beim Erhitzen löst sich der Kohlenstoff im Metall, tritt beim Abkühlen wieder heraus und ordnet sich als Graphen auf der Oberfläche an.
Eine weitere Möglichkeit der Darstellung einzelner Graphen-Lagen ist das Erhitzen hexagonaler Siliciumcarbid-Oberflächen auf Temperaturen oberhalb des Schmelzpunktes von Silizium. Aufgrund des höheren Dampfdruckes des Siliciums evaporieren die Siliciumatome schneller als die Kohlenstoff-Atome. Auf der Oberfläche bilden sich dann dünne Schichten einkristallinen Graphits, die aus wenigen Graphen-Monolagen bestehen. Dieses Verfahren ist für Anlassprozesse in Vakuum[16][17] und in einer Inertgasatmosphäre aus Argon [18]. Die Dicke und Struktur des epitaktisch gewachsenen Graphens hängt dabei empfindlich von den eingestellten Prozessparametern ab, insbesondere von der Wahl der Atmosphäre und der Struktur der Substratoberfläche sowie der Polarisation der SiC-Oberfläche.
Eigenschaften
Graphen-Flächeneinkristalle sind innerhalb der Flächen außerordentlich steif und fest. Der Elastizitätsmodul entspricht mit ca. 1020 GPa dem von normalen Graphit entlang der Basalebenen und ist fast so groß wie die des Diamants. Wissenschaftler der New Yorker Columbia University veröffentlichten 2008 weitergehende Messergebnisse, in denen sie hervorhoben, dass Graphen die höchste Rissfestigkeit aufweise, die je ermittelt wurde.[19]
Neben den Anwendungsmöglichkeiten in Verbundwerkstoff dient Graphen in der Grundlagenforschung als Modellsubstanz für zweidimensionale Kristalle: Es ist schwierig, das System in dieser Form zu erhalten, d. h. als Einzelschicht. Erst im Jahre 2004 gelang dies einer Arbeitsgruppe an der Universität Manchester, was zu kontaktierbaren „Graphen-Flocken“ führte.
Der Einzelelektronentransistor aus Graphen könnte Silizium als Transistormaterial ablösen. Forschern und Studenten am Massachusetts Institute of Technology ist es gelungen einen Graphit-Microchip herzustellen, der mit bis zu 1000 GHz operieren kann[20]. Dennoch gibt es bei der Herstellung von Graphen-Transistoren noch große Hürden zu überwinden. Graphen besitzt keine natürliche Bandlücke wie bei Halbleitern üblich. Jedoch ist es bereits gelungen, eine künstliche Bandlücke im Graphen zu erzeugen, indem man Graphen in ein maximal 10 nm breites Gate „schneidet“.[21][22][23][24][25]
Mit Hilfe von atomarem Wasserstoff, der durch eine elektrische Entladung in einem Wasserstoff-Argon-Gemisch erzeugt wird, läßt sich Graphen in Graphan umwandeln. In Graphan ist jedem Kohlenstoffatom ein Wasserstoffatom zugeordnet, und die Bindungsstruktur ähnelt dem sesselförmigen Cyclohexan. Graphan zerfällt oberhalb von 450 Grad Celsius in Graphen und Wasserstoff. Graphan ist im Gegensatz zum Graphen ein elektrischer Isolator. [26][27][28]
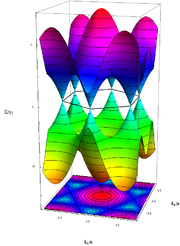 Energie der Elektronen in Graphen entsprechend ihrem Impuls
Energie der Elektronen in Graphen entsprechend ihrem Impuls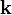 im Tight-Binding-Modell.
im Tight-Binding-Modell.Pseudo-Relativistisches Verhalten
Die elektrischen Eigenschaften von Graphen lassen sich gut durch ein Tight-Binding-Modell beschreiben. Im Rahmen dieses Modells ergibt sich die Energie der Elektronen mit Impuls
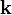 (siehe Wellenvektor) zu
(siehe Wellenvektor) zu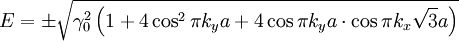 [1],
[1],
mit der Nächsten-Nachbar-Hopping-Energie
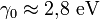 und der Gitterkonstante
und der Gitterkonstante 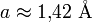 . Leitungs- und Valenzband (entsprechen Plus bzw. Minus in der obigen Dispersionsrelation) berühren sich in Graphen in sechs ausgezeichneten Punkten, den sogenannten K-Punkten, von denen jedoch nur zwei voneinander unabhängig sind (die übrigen sind durch die Gittersymmetrie zu diesen beiden äquivalent). In ihrer Umgebung hängt die Energie wie bei einem relativistischen Teilchen linear vom Impuls ab. Da die Basis zweiatomig ist, hat die Wellenfunktion sogar eine Spinorstruktur. Dies führt dazu, dass die Elektronen bei niedrigen Energien durch eine Gleichung beschrieben werden können, die formal äquivalent zur Dirac-Gleichung ist, und das zusätzlich im sogenannten chiralen Limes, d. h. für verschwindende Ruhemasse M0, was einige Besonderheiten ergibt:
. Leitungs- und Valenzband (entsprechen Plus bzw. Minus in der obigen Dispersionsrelation) berühren sich in Graphen in sechs ausgezeichneten Punkten, den sogenannten K-Punkten, von denen jedoch nur zwei voneinander unabhängig sind (die übrigen sind durch die Gittersymmetrie zu diesen beiden äquivalent). In ihrer Umgebung hängt die Energie wie bei einem relativistischen Teilchen linear vom Impuls ab. Da die Basis zweiatomig ist, hat die Wellenfunktion sogar eine Spinorstruktur. Dies führt dazu, dass die Elektronen bei niedrigen Energien durch eine Gleichung beschrieben werden können, die formal äquivalent zur Dirac-Gleichung ist, und das zusätzlich im sogenannten chiralen Limes, d. h. für verschwindende Ruhemasse M0, was einige Besonderheiten ergibt:Hier bezeichnet
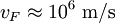 die Fermi-Geschwindigkeit in Graphen, die an die Stelle der Lichtgeschwindigkeit tritt;
die Fermi-Geschwindigkeit in Graphen, die an die Stelle der Lichtgeschwindigkeit tritt; 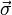 bezeichnet die Pauli-Matrizen,
bezeichnet die Pauli-Matrizen, 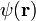 die zweikomponentige Wellenfunktion der Elektronen und E ihre Energie.[29]
die zweikomponentige Wellenfunktion der Elektronen und E ihre Energie.[29]Ungewöhnlicher Quanten-Hall-Effekt
Wegen der Besonderheiten in der Dispersion ist in diesem Material die Treppenstruktur der ganzzahligen Quanten-Hall-Plateaus,
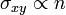 , für alle Stufen genau „um 1/2 verschoben“,
, für alle Stufen genau „um 1/2 verschoben“, 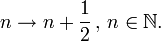 [30] Die Zwei-Valley-Struktur und die Spin-Entartung ergeben zusammen einen zusätzlichen Faktor 4.
[30] Die Zwei-Valley-Struktur und die Spin-Entartung ergeben zusammen einen zusätzlichen Faktor 4.Literatur
- Björn Trauzettel: Von Graphit zu Graphen. In: Physik Journal. 6, Nr. 7, 2007, ISSN 1617-9439, S. 39–44 ([1]).
- Mikhail I. Katsnelson: Graphene: carbon in two dimensions. In: Materials Today. 10, Nr. 1-2, 2007, ISSN 1369-7021, S. 20–27 (doi:10.1016/S1369-7021(06)71788-6).
- Phaedon Avouris, Zhihong Chen, Vasili Perebeinos: Carbon-based electronics. In: Nat Nano. 2, Nr. 10, 2007, ISSN 1748-3387, S. 605–615 (doi:10.1038/nnano.2007.300).
- Andre K. Geim, Philip Kim: Wunderstoff aus dem Bleistift. In: Spektrum der Wissenschaft. Nr. 8, 2008, S. 86–93.
Weblinks
- Jan Oliver Löfken: Graphen: Das vielleicht stabilste Papier der Welt. In: pro-physik.de. 26. Juli 2007. Abgerufen am 28. März 2008.
- Thomas Pichler: Kleinster Transistor der Welt nur ein Atom dick. In: Pressetext Schweiz (pte). 18. April 2008. Abgerufen am 28. März 2008.
- Thomas Pichler: Nano-Transistor erhöht Energieeffizienz um Faktor 50. In: Pressetext Schweiz (pte). 25. April 2008. Abgerufen am 28. März 2008.
- Andreas Stiller: Wundermaterial Graphene. In: Heise-Online. 20. Juli 2008. Abgerufen am 28. März 2008. (News-Meldung zu aktuellen Forschungsergebnissen 20. Juli 2008)
Einzelnachweise
- ↑ a b P. R. Wallace: The Band Theory of Graphite. In: Physical Review. 71, Nr. 9, 1947, S. 622-634 (doi:10.1103/PhysRev.71.622).
- ↑ Sumio Iijima: Helical microtubules of graphitic carbon. In: Nature. 354, 1991, S. 56-58 ff.
- ↑ Mitsutaka Fujita, Riichiro Saito, G. Dresselhaus, M.S. Dresselhaus: Formation of general fullerenes by their projection on a honeycomb lattice. In: Physical Review B. 45, Nr. 23, 1992, S. 13834 ff.
- ↑ L.D. Landau: Zur Theorie der Phasenumwandlungen II. In: Phys. Z. Sowjetunion. 11, 1937, S. 11.
- ↑ R.E Peierls: Quelques propriétés typiques des corpses solides. In: Ann. I. H. Poincaré. 5, 1935, S. 177-222.
- ↑ a b K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos,I. V. Grigorieva, A. A. Firsov: Electric Field Effect in Atomically Thin Carbon Films. In: Science. 306, Nr. 5696, 2004, S. 666-669 (doi:10.1126/science.1102896).
- ↑ N.D. Mermin: Crystalline Order in Two Dimensions. In: Physical Review. 176, Nr. 1, 1968, S. 250 ff (doi:10.1103/PhysRev.176.250).
- ↑ J.C. Meyer, A.K. Geim, M.I. Katsnelson, K. S. Novoselov, T. J. Booth, S. Roth: The structure of suspended graphene sheets. In: Nature. 446, 2007, S. 60 (doi:10.1038/nature05545).
- ↑ W. A. Harrison,: Electronic structure and the properties of solids: the physics of the chemical bond. W.H. Freeman and Company, San Francisco 1980, ISBN 0-7167-1000-5.
- ↑ C.E. Mortimer: Chemie. Georg Thieme Verlag, Stuttgart 2007, ISBN 978-3-13-484309-5.
- ↑ J. Wu, W. Pisula, K. Müllen: Graphenes as Potential Material for Electronics. In: Chemical Review. 107, Nr. 3, 2007, ISSN 0009-2665, S. 718-747.
- ↑ L. Zhi, K. Müllen: A bottom-up approach from molecular nanographenes to unconventional carbon materials. In: J. Mater. Chem.. 18, Nr. 18, 2008, S. 1472-1484 (doi:10.1039/b717585).
- ↑ Y. Hernandez, V. Nicolosi, M. Lotya, F. Blighe, Z. Sun, S. De, I.T. McGovern, B. Holland, M. Byrne, Y. Gunko, J. Boland, P. Niraj, G. Duesberg, S. Krishnamurti, R. Goodhue, J. Hutchison, V. Scardaci, A.C. Ferrari, J.N. Coleman: High yield production of graphene by liquid phase exfoliation of graphite. In: arXiv:0805.2850. 2008.
- ↑ A.T. N'Diaye, S. Bleikamp, P.J. Feibelman, T. Michely: Two-Dimensional Ir Cluster Lattice on a Graphene Moiré on Ir(111). In: Physical Review Letters. 97, Nr. 21, 2006, S. 718-747 (doi:10.1103/PhysRevLett.97.215501).
- ↑ P.W. Sutter, J.-I. Flege, E.A. Sutter,: Epitaxial graphene on ruthenium. In: Nature Materials. 97, Nr. 5, 2008, S. 406-411 (doi:10.1038/nmat2166).
- ↑ I. Forbeaux, J.-M. Themlin, J.-M. Debever: Heteroepitaxial graphite on 6H-SiC (0001): Interface formation through conduction-band electronic structure, overview surface reconstructions LEED, KRIPES, dispersion relation, XPS, UPS, SXPS. In: Physical Review B. Nr. 24, 1998 (doi:10.1103/PhysRevB.58.16396).
- ↑ A. Charrier, A. Coati, T. Argunova, F. Thibaudau, Y. Garreau, R. Pinchaux, I. Forbeaux, J.-M. Debever, M. Sauvage-Simkin, J.-M. Themlin: Solid-state decomposition of silicon carbide for growing ultra-thin heteroepitaxial graphite films. In: Journal of Applied Physics. 92, Nr. 5, 2002, S. 2479-2480 (doi:110.1063/1.1498962).
- ↑ K. V. Emtsev, A. Bostwick and K. Horn and J. Jobst,G. L. Kellogg, L. Ley, J.L. McChesney, T. Ohta, S.A. Reshanov, E. Rotenberg, A.K. Schmid, D. Waldmann, H. B. Weber,Th. Seyller: Atmospheric pressure graphitization of SiC(0001)- A route towards wafer-size graphene layers. In: arXiv:0808.1222. 2008.
- ↑ Changgu Lee, Xiaoding Wei, Jeffrey W. Kysar, James Hone: Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. In: Science. 321, Nr. 5887, 2008, S. 385–388 (doi:10.1126/science.1157996). )
- ↑ David Chandler: New material could lead to faster chips. In: MIT News. 19. März 2009. Abgerufen am 28. März 2009.
- ↑ Nico Ernst: Briten entwickeln Ein-Elektron-Transistor aus Graphen: Zweidimensionaler Kohlenstoff als neuer Halbleiter. In: www.golem.de. 6. März 2007. Abgerufen am 6. März 2007.
- ↑ Kevin Bullis, Wolfgang Stieler: Magischer Halbleiter-Stoff. In: Technology Review. 4, 2008 (Online ; Stand: 28. März 2008).
- ↑ Zhihong Chen, Yu-Ming Lin, Michael J. Rooks, Phaedon Avouris: Graphene nano-ribbon electronics. In: Physica E: Low-dimensional Systems and Nanostructures. 40, Nr. 2, 2007, S. 228–232 (doi:10.1016/j.physe.2007.06.020).
- ↑ Mike Rodewalt: Researchers discover method for mass production of nanomaterial graphene. In: UCLA Newsroom. 10. Nov. 2008. Abgerufen am 16. Nov. 2008.
- ↑ Luca Banszerus, Michael Schmitz, Tobias Kaufmann: Graphen. (PDF ; Stand: 16. Nov. 2008; Jugend-forscht-Arbeit).
- ↑ Werkstoffe: Aus Graphen wird Graphan. In: Physik in unserer Zeit. 40, Nr. 2, 2009, S. 70 (doi:10.1002/piuz.200990033).
- ↑ James Urquhart: Graphene to graphane by chemical conversion. 29. Jan. 2009. Abgerufen am 26. Apr. 2009. (Nachrichtenmeldung, englisch)
- ↑ D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim, K. S. Novoselov: Control of Graphene's Properties by Reversible Hydrogenation: Evidence for Graphane. In: Science. 323, Nr. 5914, 2009, S. 610-613 (doi:10.1126/science.1167130).
- ↑ A. H. Castro Neto, F. Guinea, N. M. R Peres, K. S. Novoselov, A. K. Geim: The electronic properties of graphene. In: Arxiv preprint. 2007 (arXiv:0709.1163v2).
- ↑ A. K. Geim, K.S. Novoselov: The rise of graphene. In: Nature Materials. Nr. 6, 2007, S. 183–191 (doi:10.1038/nmat1849).
Wikimedia Foundation.