Gradientfeld

Ein Gradientenfeld ist ein Vektorfeld, das der Gradient einer „Stammfunktion“ sein kann. Das Vektorfeld F ist also genau dann ein Gradientenfeld, wenn es ein Skalarfeld G gibt mit 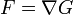$F = \nabla G$. Dann heißt G Potential.

Gradientenfelder zeichnen sich durch folgenden Eigenschaften aus:

1. Kurvenintegrale sind wegunabhängig, nur die Anfangs- und Endposition sind relevant.
2. Daraus folgt, dass alle geschlossenen Kurvenintegrale verschwinden.
3. Gradientenfelder sind rotationsfrei. (wirbelfrei)

Integrabilitätsbedingung

→ Hauptartikel: Integrabilitätsbedingung

Sei 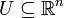$U \subseteq \mathbb{R}^n$ offene und sternförmige Menge und 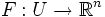$F: U \to \mathbb{R}^n$ stetig differenzierbar, so ist F genau dann ein Gradientenfeld, wenn die Integrabilitätsbedingung 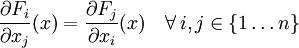$\frac{\partial F_i}{\partial x_j}(x) = \frac{\partial F_j}{\partial x_i} (x) \quad \forall\, i,j \in \{1 \dots n \}$ auf U erfüllt ist. Eine äquivalente Schreibweise ist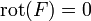 $\operatorname{rot}(F)=0$

Im Zwei- und Dreidimensionalen genügt, dass U eine offene und einfach zusammenhängende Menge ist. Die Integrabilitätsbedingung schreibt sich dann:

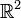
• im 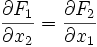$\mathbb{R}^2$ $\frac{\partial F_1}{\partial x_2} = \frac{\partial F_2}{\partial x_1}$ (nach dem Satz von Schwarz)
• im 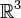$\mathbb{R}^3$ zusätzlich 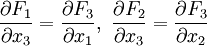$\frac{\partial F_1}{\partial x_3} = \frac{\partial F_3}{\partial x_1},\ \frac{\partial F_2}{\partial x_3} = \frac{\partial F_3}{\partial x_2}$ ^[1]

Die Integrabilitätsbedingung ist notwendig aber nicht hinreichend.

Potential in der Physik

In der Physik besitzt das Potential das entgegengesetzte Vorzeichen: $F = - \nabla G$

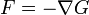
Siehe auch

• Konservatives Feld
• Potentialfeld

Einzelnachweise

1. ↑ Königsberger, Analysis 2, Springer Verlag, 5. Auflage, ISBN 3-540-20389-3, Korollar Seite 193