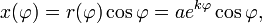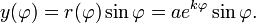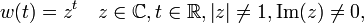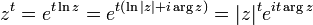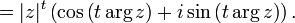- Gleichwinklige Spirale
-
Eine logarithmische Spirale ist eine Spirale, die mit jeder Umdrehung den Abstand von ihrem Mittelpunkt, dem Pol, um den gleichen Faktor vergrößert. In umgekehrter Drehrichtung schlingt sich die Kurve mit abnehmendem Radius immer enger um den Pol. Jede Gerade durch den Pol schneidet die logarithmische Spirale stets unter dem gleichen Winkel. Wegen dieser Eigenschaft spricht man auch von einer gleichwinkligen Spirale.
Inhaltsverzeichnis
Mathematische Darstellung
Am leichtesten lässt sich eine logarithmische Spirale in Polarkoordinaten
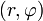 angeben:
angeben: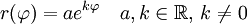
- mit k = const. als Steigung der Spirale, und dem Steigungswinkel α, tanα = k
In kartesischen Koordinaten ergibt sich:
Namensgebend ist die implizite Darstellung:
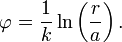
 lässt sich hierbei als normierter Radius verstehen.
lässt sich hierbei als normierter Radius verstehen.
In der komplexen Ebene lässt sich jede logarithmische Spirale sogar noch einfacher darstellen:
denn
Eigenschaften
Die logarithmische Spirale hat eine Reihe einzigartiger Eigenschaften, weshalb sie von einem ihrer größten Liebhaber, Jakob Bernoulli, auch als spira mirabilis („wundersame Spirale“) bezeichnet wurde:
- alle durch den Pol gehenden Geraden schneiden die Kurve – also ihre Tangenten – unter dem gleichen Tangentenwinkel
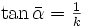 bzw.
bzw. 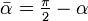 (siehe Abbildung)
(siehe Abbildung) - die Spirale umkreist den Ursprung unendlich oft, ohne ihn zu erreichen (asymptotischer Punkt)
- obwohl unendlich viele Drehungen bis zum Erreichen des Pols benötigt werden, ist die Länge der Kurve von jedem Kurvenpunkt bis zum Pol endlich
- mit jeder Windung wächst der Radius um einen konstanten Faktor:
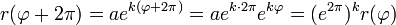
- mit e2π ≈ 535,5 in einer Potenz der Steigung k (daher ergeben nur relativ flache Spiralen mit k ≪ 1 „hübsche“ Schnecken). Diese Eigenschaft unterscheidet alle logarithmischen Spiralen von den archimedischen, die sich bei jeder Windung um eine Konstante ausdehnen (ihre Steigung nimmt dabei ab)
- die logarithmische Spirale ist – in Verallgemeinerung der obigen Herleitung – selbstähnlich (invariant) gegenüber einer zentrischen Streckung um den Faktor ekγ bei gleichzeitiger Drehung um den Winkel γ
- Das gilt für die konstant wachsende Archimedesspirale nicht: Darum scheinen rotierende Archimedesspiralen „nach außen“ zu wandern, aber logarithmische perspektivisch auf den Beobachter zuzukommen.
- die Kurve ist ihre eigene Evolute
- die Kurve ist ihre eigene Brennlinie (Kaustik)
- die Kurve ist ihre eigene Fußpunktkurve
- eine Inversion der Kurve (
 ) führt zu Drehung und Spiegelung der Kurve an der Y-Achse (für a = 1 nur zur Spiegelung); aus einer linksdrehenden logarithmischen Spirale wird eine rechtsdrehende und umgekehrt
) führt zu Drehung und Spiegelung der Kurve an der Y-Achse (für a = 1 nur zur Spiegelung); aus einer linksdrehenden logarithmischen Spirale wird eine rechtsdrehende und umgekehrt - alle Spiralen gleicher Steigung sind ähnlich
- Für
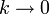 nähert sich die Spirale immer mehr einem Kreis des Radius a an, der die Kurvengleichung für k = 0 (Schnittwinkel 90 Grad) erfüllt. Dass der Kreis ein Spezialfall der logarithmischen Spirale ist, ist insbesondere in der Kugelgeometrie bedeutend.
nähert sich die Spirale immer mehr einem Kreis des Radius a an, der die Kurvengleichung für k = 0 (Schnittwinkel 90 Grad) erfüllt. Dass der Kreis ein Spezialfall der logarithmischen Spirale ist, ist insbesondere in der Kugelgeometrie bedeutend.
Spezialfälle und Näherungen
Die Goldene Spirale ist ein Sonderfall der logarithmischen Spirale, die als Spezialität das Teilungsverhältnisses des Goldenen Schnittes als Steigung verwendet, und durch Verwendung von rekursiver Teilung eines Goldenen Rechtecks in je ein Quadrat und ein weiteres, kleineres Goldenes Rechteck, in sich trägt.
Jede logarithmische Spirale lässt sich auch durch einen Polygonzug approximieren, bei dem Dreiecke mit einem gleichen Winkel (k), und jeweils der kürzeren Seite so lang wie die längere Seite des vorigen Dreiecks. Eine Erweiterung dieses Gedankenganges gilt auch für gewisse irreguläre Polygone, die sich aneinanderlegen lassen. Dieses Bauprinzip ist in der Natur verbreitet, und liefert im allgemeinen mehrgängige Spiralen.
Formeln
siehe auch: Formelsammlung Geometrie
Formeln zur Logarithmischen Spirale Funktion 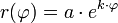
Steigung 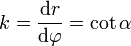
Krümmungsradius 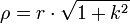
Bogenelement 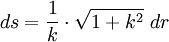
Flächenelement 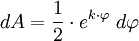
Vorkommen
In der belebten Natur finden sich zahlreiche Beispiele logarithmischer Spiralen mit diversen Steigungen, wie beispielsweise durch Wachstum entstandene Schneckenhäuser oder die Anordnung von Kernen in der Blüte einer Sonnenblume.
Ein Fluginsekt orientiert sich bei einem nächtlichen Flug am Stand des (weitentfernten) Mondes, indem es den Winkel zu ihm konstant hält. Durch eine (punktuelle nahe) Straßenlaterne wird die Flugkurve jedoch regelmäßig korrigiert, so dass sie zu einer logarithmischen Spirale wird, in deren Zentrum sich die Straßenlaterne befindet.
Daneben finden sich annähernd logarithmisch spiralförmige Strukturen in allen dynamischen Mehrkörpersystemen und fluiddynamischen Systemen (Wirbelbildung bei ausreichend großem Geschwindigkeitsgradient) sowie in der Technik (z. B. Hinterdrehen).
Der Erzählung nach war es ein Wunsch Jakob Bernoullis, dass seine geliebte logarithmische Spirale mit der Inschrift eadem mutata resurgo („Verwandelt kehr' ich als dieselbe wieder“) auf seinen Grabstein eingemeißelt werden sollte. Der zuständige Steinmetz meißelte nach dem Tod Bernoullis zwar eine Spirale auf dessen Grabstein, allerdings handelte es sich (vermutlich aus Unwissenheit oder um sich Arbeit zu sparen) um eine Archimedische Spirale, für die keine der genannten Eigenschaften zutrifft. Bernoullis Grabstein kann noch heute im Kreuzgang des Münsters zu Basel besichtigt werden.
Schnitt eine Nautilus-Schale
Whirlpool-Galaxie, eine typische Spiralgalaxie
Tiefdruckwirbel über Island
Weblinks
- Mathworld (englisch)
Wikimedia Foundation.