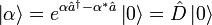Glauber-Zustand

Kohärente Zustände (vgl. auch kohärente Strahlung) sind quantenmechanische Zustände unbestimmter Teilchenzahl, meist bei Bosonen.

Wie R.J. Glauber 1963 zeigte, lässt sich die elektromagnetische Welle einer Laser-Mode am besten durch kohärente Zustände beschreiben.

Kohärente Zustände kommen klassischen elektromagnetischen Wellen sehr nahe, weil der Erwartungswert der elektrischen Feldstärke die Form einer klassischen elektromagnetischen Welle hat, unabhängig vom Erwartungswert der Teilchenzahl.

Misst man in einem kohärenten Zustand die Teilchenzahl jeweils in einem festen Zeitintervall, so erhält man Messwerte, die einer Poisson-Verteilung genügen.

Beschreibung im Fockraum

Ein idealer kohärenter Zustand bei der quantenfeldtheoretischen Behandlung der Photonen, Elektronen, etc. ist stets eine Überlagerung von Zuständen verschiedener Teilchenzahl, er enthält sogar (verschwindend geringe) Anteile beliebig hoher Teilchenzahl. In Fock-Raum-Schreibweise (nach Wladimir Alexandrowitsch Fock) ergibt sich der kohärente Zustand 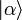$|\alpha\rangle$ als unendliche Linearkombination von Zuständen fester Teilchenzahl (Fock-Zustände) 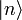$|n\rangle$ nach:

$|\alpha\rangle=e^{-{|\alpha|^2\over2}}\sum_{n=0}^{\infty}{\alpha^n\over\sqrt{n!}}|n\rangle$

Dabei ist α eine beliebige nichtverschwindende komplexe Zahl, die den kohärenten Zustand vollständig definiert. Die Wahrscheinlichkeit eine Besetzung von genau n Teilchen zu messen ist

$P(n)= |\langle n|\alpha \rangle|^2 = \frac{|\alpha|^{2n}}{n!}e^{-|\alpha|^2}$

Die Verteilung entspricht also der Poisson-Verteilung. Demnach ist | α | ² der Erwartungswert der Besetzungszahl des kohärenten Zustandes. Der kohärente Zustand kann auf einfache Weise durch Anwendung eines unitären "Verschiebungsoperators" 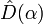$\hat{D}(\alpha)$ aus dem unbesetzten Zustand 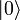$|0\rangle$ des Systems erzeugt werden (siehe Abschnitt Herleitung):

$|\alpha\rangle=\hat{D}(\alpha)|0\rangle=\exp{\left(\alpha \hat{a}^\dagger - \alpha^* \hat{a}\right)}|0\rangle$

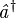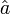Dabei sind $\mathit{\hat{a}^\dagger}$ und $\hat{a}\$ die Auf- bzw. Absteigeoperatoren des Fock-Zustandes.

Eigenschaften

Wichtige Eigenschaften eines kohärenten Zustandes 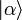$|\alpha\rangle$ sind:

• Normierung: Der Vorfaktor des kohärenten Zustandes dient also der Normierung. $\langle\alpha|\alpha\rangle = 1$
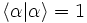
• Orthogonalität: Kohärente Zustände sind nicht orthogonal. $\langle\beta|\alpha\rangle \ne \delta(\alpha - \beta)$
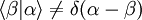
• Der kohärente Zustand ist ein "rechtsseitiger" Eigenzustand des Vernichtungsoperators 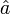$\hat a$. Es gilt: $\hat a|\alpha\rangle = \alpha |\alpha\rangle$.

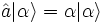Der Bra-Vektor ist ein linksseitiger Eigenzustand des Erzeugungsoperators mit komplex-konjugiertem Eigenwert: $\langle \alpha | \hat a ^\dagger= \alpha ^{*} \langle \alpha |$

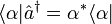
Der Vernichtungsoperator a kann im Gegensatz zum Erzeugungsoperator 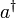$a^\dagger$ tatsächlich Eigenzustände (Rechtseigenzustände) besitzen. Der Erzeugungsoperator erhöht die minimale Teilchenzahl eines Zustandes im Fockraum um eins; der damit entstandene Zustand kann also nicht der ursprüngliche sein. Dagegen verringert der Vernichtungsoperator die maximale Teilchenzahl um eins; da ein Zustand im Fockraum aber Komponenten aller Teilchenzahlen beinhalten kann (wie es beim kohärenten Zustand zutrifft), ist damit nicht verboten, dass a Eigenzustände besitzt.

• Kohärente Zustände besitzen minimale Unschärfe: $\frac{1}{4}|\langle\alpha|[\hat p,\hat x]|\alpha\rangle|^2 = \frac{\hbar^2}{4}$
• Kohärente Zustände bleiben kohärent

In der Quantenelektrodynamik ist der kohärente Zustand ein Eigenzustand des Operators des Vektorfeldes 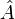$\hat A$ (oder, gleichbedeutend, des elektrischen Feldes 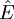$\hat E$). In einem kohärenten Zustand verschwinden also die Quantenfluktuationen des elektrischen Feldes.

Geschichte

Der o.g. kohärente Zustand wurde von Erwin Schrödinger entdeckt als dieser nach einem Zustand des quantenmechanischen harmonischen Oszillators suchte, der dem des klassischen harmonischen Oszillators entspricht und von Roy J. Glauber auf den Fockraum übertragen. Der kohärente Zustand entspricht demnach einem gaußschen Wellenpaket das im harmonischen Potential hin- und herläuft ohne Orts- oder Impulsunschärfe zu verändern.

Herleitung

Im Folgenden wird gezeigt, dass die kohärenten Zustände Eigenzustände des Vernichtungsoperators sind:

$\hat{a}\left|\alpha\right\rangle =\alpha\left|\alpha\right\rangle$

Die Fockzustände 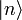$|n\rangle$ bilden ein vollständiges Orthonormalensystem, also kann man jeden Zustand nach ihnen entwickeln:

$|\alpha\rangle=\sum\limits _{n=0}^{\infty}|n\rangle\underbrace{\langle n|\alpha\rangle}_{b_{n}}=\sum\limits _{n=0}^{\infty}b_{n}|n\rangle$

Nun betrachtet man die linke Seite der Eigenwertgleichung, wobei 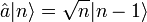$\hat{a}|n\rangle=\sqrt{n}|n-1\rangle$ und $\hat{a}|0\rangle=0$:

$\hat{a}|\alpha\rangle=\sum\limits _{n=0}^{\infty}b_{n}\hat{a}|n\rangle=\sum\limits _{n=1}^{\infty}b_{n}\sqrt{n}\,|n-1\rangle=\sum\limits _{n=0}^{\infty}b_{n+1}\sqrt{n+1}\,|n\rangle$

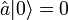Die rechte Seite der Eigenwertgleichung:

$\alpha|\alpha\rangle=\sum\limits _{n=0}^{\infty}b_{n}\alpha|n\rangle$

Aus der Gleichheit beider Seiten gewinnt man eine Rekursionsbeziehung $b_{n+1}\sqrt{n+1}=b_{n}\alpha$

$b_{n}=\frac{\alpha}{\sqrt{n}}\,b_{n-1}=\frac{\alpha^{n}}{\sqrt{n!}}\,b_{0}$

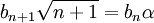
Nun nutzt man die Normierungsbedingung der kohärenten Zustände aus, um b₀ zu bestimmen:

$1=\langle\alpha|\alpha\rangle=\sum\limits _{m,n=0}^{\infty}b_{m}^{*}b_{n}\underbrace{\langle m|n\rangle}_{\delta_{mn}}=\sum\limits _{n=0}^{\infty}|b_{n}|^{2}=\sum\limits _{n=0}^{\infty}\frac{|\alpha|^{2n}}{n!}|b_{0}|^{2}=e^{|\alpha|^{2}}|b_{0}|^{2}$

Radizieren liefert b₀, wobei eine komplexe Phase zu null und somit b₀ reell gewählt wird:

$b_{0}=e^{-\frac{1}{2}|\alpha|^{2}}$

Dies ergibt eingesetzt in obige Entwicklung die Darstellung der kohärenten Zustände:

$|\alpha\rangle=\sum\limits _{n=0}^{\infty}b_{n}|n\rangle=b_{0}\sum\limits _{n=0}^{\infty}\frac{\alpha^{n}}{\sqrt{n!}}|n\rangle=e^{-\frac{\left|\alpha\right|^{2}}{2}}\sum\limits _{n=0}^{\infty}\frac{\alpha^{n}}{\sqrt{n!}}\left|n\right\rangle$

Nutzt man noch aus, dass die Fockzustände 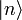$|n\rangle$ sich durch Anwendung des Erzeugungsoperators aus dem Vakuumzustand 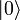$|0\rangle$ ergeben 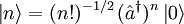$\left|n\right\rangle =(n!)^{-1/2}\,(\hat{a}^{\dagger})^{n}\left|0\right\rangle$ und dann noch dass die Anwendung des Vernichtungsoperators auf den Vakuumzustand eine Null produziert 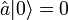$\hat{a}|0\rangle=0$ bzw. 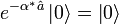$e^{-\alpha^{*}\hat{a}}\left|0\right\rangle =\left|0\right\rangle$, dann erhält man:

$\left|\alpha\right\rangle =e^{-\frac{\left|\alpha\right|^{2}}{2}}\sum\limits _{n=0}^{\infty}\frac{\alpha^{n}}{\sqrt{n!}}\frac{\left(\hat{a}^{\dagger}\right)^{n}}{\sqrt{n!}}\left|0\right\rangle =e^{-\frac{\left|\alpha\right|^{2}}{2}}e^{\alpha\hat{a}^{\dagger}}\left|0\right\rangle=e^{-\frac{\left|\alpha\right|^{2}}{2}}e^{\alpha\hat{a}^{\dagger}}e^{-\alpha^{*}\hat{a}}\left|0\right\rangle$

Mit der Baker-Campbell-Hausdorff-Formel $e^{\hat{A}}e^{\hat{B}}=e^{\hat{A}+\hat{B}}e^{[\hat{A},\hat{B}]/2}$ kann man das Produkt der beiden Exponentialfunktionen zusammenfassen, wobei $[\hat{a}^{\dagger},\hat{a}]=-1$:

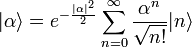
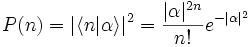
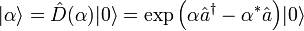
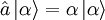
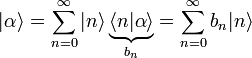
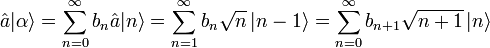
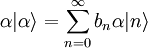
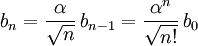
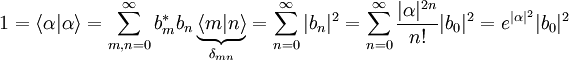
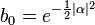
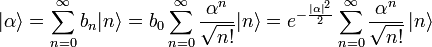
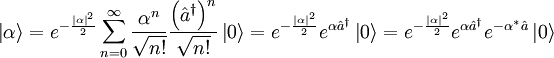
$e^{\alpha\hat{a}^{\dagger}}e^{-\alpha^{*}\hat{a}}=e^{\alpha\hat{a}^{\dagger}-\alpha^{*}\hat{a}}e^{-\alpha\alpha^{*}[\hat{a}^{\dagger},\hat{a}]/2}=e^{\alpha\hat{a}^{\dagger}-\alpha^{*}\hat{a}}e^{|\alpha|^{2}/2}$

Somit

$\left|\alpha\right\rangle =e^{\alpha\hat{a}^{\dagger}-\alpha^{*}\hat{a}}\left|0\right\rangle=\hat{D}\left|0\right\rangle$

Literatur

• R.J. Glauber, Phys. Rev. 131, 2766, 1963

Siehe auch

• Kohärente Strahlung
• Kohärenz
• Fockraum