- Fraktale Geometrie
-
 Berühmtes Fraktal: die Mandelbrot-Menge (sogenanntes „Apfelmännchen“)
Berühmtes Fraktal: die Mandelbrot-Menge (sogenanntes „Apfelmännchen“)Fraktal ist ein von Benoît Mandelbrot (1975) geprägter Begriff (lat. fractus: gebrochen, von frangere: brechen, in Stücke zerbrechen), der natürliche oder künstliche Gebilde oder geometrische Muster bezeichnet, die einen hohen Grad von Skaleninvarianz bzw. Selbstähnlichkeit aufweisen. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst besteht. Geometrische Objekte dieser Art unterscheiden sich in wesentlichen Aspekten von gewöhnlichen glatten Figuren.
Der Begriff Fraktal kann sowohl substantivisch wie adjektivisch verwendet werden. Das Gebiet der Mathematik, in dem Fraktale und ihre Gesetzmäßigkeiten untersucht werden, heißt fraktale Geometrie und ragt in mehrere andere Bereiche hinein, wie Funktionentheorie, Berechenbarkeitstheorie und dynamische Systeme. Wie der Name schon andeutet, wird der klassische Begriff der euklidischen Geometrie erweitert, was sich auch in den gebrochenen und nicht natürlichen Dimensionen vieler Fraktale widerspiegelt. Neben Mandelbrot gehören Waclaw Sierpinski und Gaston Maurice Julia zu den namensgebenden Mathematikern.
Durch ihren Formenreichtum und dem damit verbundenen ästhetischen Reiz spielen sie in der digitalen Kunst eine gewisse Rolle und haben dort das Genre der sogenannten Fraktalkunst hervorgebracht. Ferner werden sie bei der computergestützten Simulation formenreicher Strukturen wie beispielsweise realitätsnaher Landschaften eingesetzt.
Inhaltsverzeichnis
Fraktale Dimension
 Ein kleiner Ausschnitt am Rand der Mandelbrotmenge. Hier zeigt sie Ähnlichkeit mit einer Julia-Menge
Ein kleiner Ausschnitt am Rand der Mandelbrotmenge. Hier zeigt sie Ähnlichkeit mit einer Julia-MengeIn der traditionellen Geometrie ist eine Linie eindimensional, eine Fläche zweidimensional und ein Raum dreidimensional. Für fraktale Gebilde lässt sich die Dimensionalität nicht so einfach angeben: Führt man beispielsweise eine Rechenoperation für ein fraktales Linienmuster tausende von Malen fort, so füllt sich mit der Zeit die gesamte Zeichenfläche (etwa der Bildschirm des Computers) mit Linien, und das eindimensionale Gebilde nähert sich einem zweidimensionalen.
Mandelbrot benutzte den Begriff der verallgemeinerten Dimension nach Hausdorff und stellte fest, dass fraktale Gebilde meist eine nicht-ganzzahlige Dimension aufweisen. Sie wird auch als fraktale Dimension bezeichnet. Daher führte er folgende Definition ein:
- Ein Fraktal ist eine Menge, deren Hausdorff-Dimension größer ist als ihre Lebesgue’sche Überdeckungsdimension.
Jede Menge mit nicht-ganzzahliger Dimension ist also ein Fraktal. Die Umkehrung gilt nicht, Fraktale können auch ganzzahlige Dimension besitzen, beispielsweise die Brownsche Bewegung.
Besteht ein Fraktal aus einer bestimmten Anzahl von verkleinerten Kopien seiner selbst, und ist dieser Verkleinerungsfaktor für alle Kopien derselbe, verwendet man die Ähnlichkeitsdimension D, die in solchen einfachen Fällen der anschaulichen Berechnung der Hausdorff-Dimension entspricht.
Etwas abstrakter betrachtet wird diese Dimension, führt man folgende Größen ein:
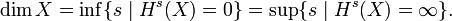
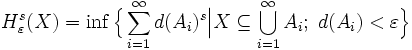
Wobei ebenjenes X der fraktalen Dimension entspricht.
Beispiele
Die einfachsten Beispiele für selbstähnliche Objekte sind Strecken, Parallelogramme (u. a. Quadrate) und Würfel, denn sie können durch zu ihren Seiten parallele Schnitte in verkleinerte Kopien ihrer selbst zerlegt werden. Diese sind jedoch keine Fraktale, weil ihre Ähnlichkeitsdimension und Lebesgue’sche Überdeckungsdimension übereinstimmen. Ein Beispiel für ein selbstähnliches Fraktal ist das Sierpinski-Dreieck, welches aus drei auf die Hälfte verkleinerten Kopien seiner selbst aufgebaut ist. Es hat somit die Ähnlichkeitsdimension
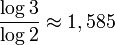 , während die Lebesgue’sche Überdeckungsdimension gleich 1 ist.
, während die Lebesgue’sche Überdeckungsdimension gleich 1 ist.Die Selbstähnlichkeit muss nicht perfekt sein, wie die erfolgreiche Anwendung der Methoden der Fraktale Geometrie auf natürliche Gebilde wie Bäume, Wolken, Küstenlinien usw. zeigen. Die genannten Objekte sind in mehr oder weniger starkem Maß selbstähnlich strukturiert (ein Baumzweig sieht ungefähr so aus wie ein verkleinerter Baum), die Ähnlichkeit ist jedoch nicht streng, sondern stochastisch. Im Gegensatz zu Formen der euklidischen Geometrie, die bei einer Vergrößerung oft flacher und damit einfacher werden (etwa ein Kreis), können bei Fraktalen immer komplexere und neue Details auftauchen.
Fraktale Muster werden oft durch rekursive Operationen erzeugt. Auch einfache Erzeugungsregeln ergeben nach wenigen Rekursionsschritten schon komplexe Muster.
Dies ist zum Beispiel am Pythagoras-Baum zu sehen. Ein solcher Baum ist ein Fraktal, welches aus Quadraten aufgebaut ist, die so angeordnet sind wie im Satz des Pythagoras definiert.
Ein weiteres Fraktal ist das Newton-Fraktal, es wird berechnet über das Newton-Verfahren, das zur Nullstellenberechnung verwendet wird.
Ein Fraktal im dreidimensionalen Raum ist der Menger-Schwamm.
Verfahren zur Erzeugung von Fraktalen
Fraktale können auf viele verschiedene Arten erzeugt werden, doch alle Verfahren enthalten ein rekursives Vorgehen. Mögliche Verfahren sind:
- Die Iteration von Funktionen ist die einfachste und bekannteste Art, Fraktale zu erzeugen; die Mandelbrot-Menge entsteht so. Eine besondere Form dieses Verfahrens sind IFS–Fraktale (Iterierte Funktionensysteme), bei denen mehrere Funktionen kombiniert werden. So lassen sich natürliche Gebilde erstellen.
- Dynamische Systeme erzeugen fraktale Gebilde, sogenannte seltsame Attraktoren.
- L-Systeme, die auf wiederholter Textersetzung beruhen, eignen sich gut zur Modellierung natürlicher Gebilde wie Pflanzen und Zellstrukturen.
Fraktale, die sich geometrisch konstruieren lassen
Fraktal L-System Winkel Strecken-Verhältnis Visualisierung Drachenkurve F → R oder F → L R → +R--L+ L → -R++L-
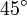
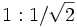
Gosper-Kurve F → R oder F → L R → R+L++L-R--RR-L+ L → -R+LL++L+R--R-L
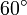
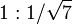
Hilbert-Kurve X X → -YF+XFX+FY- Y → +XF-YFY-FX+
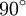
1:1 / 2 Koch-Flocke F--F--F F → F+F--F+F
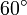
1:1 / 3 Peano-Kurve X X → XFYFX+F+YFXFY-F-XFYFX Y → YFXFY-F-XFYFX+F+YFXFY
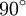
Peano-Kurve F F → F-F+F+F+F-F-F-F+F
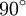
1:1 / 3 Penta Plexity F++F++F++F++F F → F++F++F|F-F++F
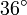
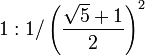
Pfeilspitze F → R oder F -> L R → -L+R+L- L → +R-L-R+
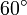
1:1 / 2 Sierpinski-Dreieck FXF--FF--FF X → --FXF++FXF++FXF-- F → FF
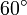
Dreieck F--F--F F → F--F--F--ff f → ff
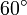
1:1 / 3 Sierpinski-Teppich F F → F+F-F-FF-F-F-fF f → fff
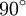
1:1 / 3 Lévy-C-Kurve F F → +F--F+
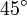
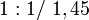
- Erklärung des L-Systems:
Das optionale, also nicht notwendige F wird im allgemeinen als Strecke benutzt, die durch eine Anweisungsfolge ersetzt wird. Wie das F stehen auch andere groß geschriebene Buchstaben wie R und L für einen Streckenabschnitt, der ersetzt wird. + und - stehen für einen bestimmten Winkel, der im Uhrzeigersinn, oder gegen den Uhrzeigersinn läuft. Das Symbol | bezeichnet eine Kehrtwendung des Zeichenstiftes, also eine Drehung um 180°. Gegebenenfalls setzt man dafür ein entsprechendes Vielfaches des Drehwinkels ein.
-
- Beispiel Drachenkurve:
F → R R → +R--L+ L → -R++L-
F ist eine einfache Strecke zwischen zwei Punkten. F -> R heißt, dass die Strecke F durch R ersetzt wird. Dieser Schritt ist notwendig, da es zwei rekursive Ersetzungen R und L besitzt, die sich gegenseitig enthalten. Im weiteren wird wie folgt ersetzt:
R +R--L+ +(+R--L+)--(-R++L-)+ +(+(+R--L+)--(-R++L-)+)--(-(+R--L+)++(-R++L-)-)+ . . .
Ab einem bestimmten Abschnitt muss dieser Ersetzungsprozess abgebrochen werden, um eine Grafik zu bekommen:
+(+(+r--l+)--(-r++l-)+)--(-(+r--l+)++(-r++l-)-)+
Wobei r und l jeweils eine fest vorgegebene Strecke darstellen.
Fraktale in der Natur
 Fraktaler Blumenkohl
Fraktaler BlumenkohlFraktale Konzepte findet man auch in der Natur. Dabei ist jedoch die Anzahl der Stufen von selbstähnlichen Strukturen begrenzt und beträgt oft nur 3-5. Typische Beispiele aus der Biologie sind die fraktalen Strukturen bei der grünen Blumenkohlzüchtung Romanesco und bei den Farnen. Auch der Blumenkohl hat einen fraktalen Aufbau, wobei man es diesem Kohl auf den ersten Blick häufig gar nicht ansieht. Es gibt aber immer wieder einige Blumenkohlköpfe, die dem Romanesco im fraktalen Aufbau sehr ähnlich sehen.
Weit verbreitet sind fraktale Strukturen ohne strenge sondern mit statistischer Selbstähnlichkeit. Dazu zählen beispielsweise Bäume, der Blutkreislauf, Flusssysteme und Küstenlinien. Im Fall der Küstenlinie ergibt sich als Konsequenz die Unmöglichkeit einer exakten Bestimmung der Küstenlänge. Je genauer man die Feinheiten des Küstenverlaufes vermisst, umso größer ist die Länge, die man erhält. Im Falle eines mathematischen Fraktals, wie beispielsweise der Kochkurve, wäre sie unbegrenzt.
Fraktale finden sich auch als Erklärungsmodelle für chemische Reaktionen. Systeme wie die Oszillatoren (Standardbeispiel Belousov-Zhabotinsky-Reaktion) lassen sich einerseits als Prinzipbild verwenden, andererseits aber auch als Fraktale erklären. Ebenso findet man fraktale Strukturen auch im Kristallwachstum und bei der Entstehung von Mischungen, wenn man z. B. einen Tropfen Farblösung in ein Glas Wasser gibt.
Das Auffasern von Bast lässt sich über die fraktale Geometrie von Naturfaserfibrillen erklären. Insbesondere ist die Flachsfaser eine fraktale Faser.
Literatur
- Herbert Voß: Chaos und Fraktale selbst programmieren, franzis', ISBN 3-7723-7003-9
- Horst Halling / Rolf Möller: Mathematik fürs Auge - Eine Einführung in die Welt der Fraktale, Spektrum, ISBN 3-86025-427-8
- Benoît B. Mandelbrot: Die fraktale Geometrie der Natur, Birkhäuser, ISBN 3-7643-2646-8
- Heinz-Otto Peitgen, Peter H. Richter: The Beauty of Fractals. Images of Complex Dynamical Systems, Springer, ISBN 0-387-15851-0 bzw. ISBN 3-540-15851-0
- Heinz-Otto Peitgen, Dietmar Saupe: The Science of Fractal Images, ISBN 0-387-96608-0
- Kenneth Falconer: FRACTAL GEOMETRY. Mathematical Foundations and Applications, Wiley 1997
Weblinks
- Fractalizer.de Website des Fraktalprogramms "Fractalizer"
- Quaternionische Fraktale (PDF), Abschlussarbeit über quaternionische (4D) Fraktale
- Die Ästhetik der Fraktale, (PDF), Rafael Reiter
- Fraktale in der Natur (engl.)
- Mandelbrot Fractal Explorer Erforschung der Mandelbrot-Menge mit MapClient (OpenLayers)
- Einige Fraktale und in Basic geschriebene Programme, die diese erzeugen
- Javabasierter Fraktalgenerator und interaktive Fraktal-Galerie. (Ein aktuelles Java-Browser-Plug-in ist erforderlich)
- YaFGen — Ein Fraktalgenerator für verschiedene Typen, geschrieben in der Programmiersprache Java.
- Visual Basic Programm Barnsely Farn und mehr - Programm zum Erzeugen von Farnblättern und vielem mehr, incl. Facharbeit
Wikimedia Foundation.















.jpg)