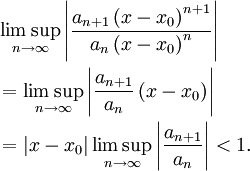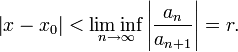Formel von Cauchy-Hadamard
- Formel von Cauchy-Hadamard
-
Als Konvergenzradius einer Potenzreihe der Form
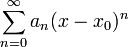
ist die größte Zahl r definiert, für welche die Potenzreihe für alle x mit | x − x0 | < r konvergiert. Falls sie auf der ganzen komplexen Zahlenebene konvergiert, sagt man, der Konvergenzradius ist unendlich.
Wird eine reelle Potenzreihe betrachtet, deren Koeffizienten ak reelle Zahlen sind, und sind auch  reell, so ist der Konvergenzbereich nach Auflösung der Betragsungleichung das Intervall
reell, so ist der Konvergenzbereich nach Auflösung der Betragsungleichung das Intervall 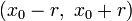 sowie möglicherweise einer der oder beide Randpunkte. Für Potenzreihen im Komplexen, das heißt, alle diese Größen können komplexe Zahlen sein, besteht der Konvergenzbereich dieser Funktionenreihe aus dem Inneren der Kreisscheibe um den Mittelpunkt x0 und mit Radius r sowie möglicherweise aus einigen Randpunkten.
sowie möglicherweise einer der oder beide Randpunkte. Für Potenzreihen im Komplexen, das heißt, alle diese Größen können komplexe Zahlen sein, besteht der Konvergenzbereich dieser Funktionenreihe aus dem Inneren der Kreisscheibe um den Mittelpunkt x0 und mit Radius r sowie möglicherweise aus einigen Randpunkten.
Der Konvergenzradius lässt sich mit der Formel von Cauchy-Hadamard berechnen. Es gilt
![r=\frac{1}{\limsup\limits_{n\rightarrow\infty}\left(\sqrt[n]{|a_n|}\right)}.](/pictures/dewiki/57/9026caee3746222ff14d9c7c63976d95.png)
Wenn ab einem bestimmten Index alle an von 0 verschieden sind und der folgende Limes existiert, dann kann der Konvergenzradius einfacher durch
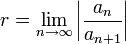
berechnet werden. Diese Formel ist aber nicht immer anwendbar, zum Beispiel bei der Koeffizientenfolge 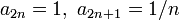 : Die zugehörige Reihe hat Konvergenzradius 1, aber der angegebene Limes existiert nicht. Die Formel von Cauchy-Hadamard ist dagegen immer anwendbar.
: Die zugehörige Reihe hat Konvergenzradius 1, aber der angegebene Limes existiert nicht. Die Formel von Cauchy-Hadamard ist dagegen immer anwendbar.
Folgerungen aus dem Konvergenzradius:
- Ist | x − x0 | < r, so ist die Potenzreihe absolut konvergent.
- Ist | x − x0 | > r, so ist die Potenzreihe divergent.
- Ist | x − x0 | = r, so kann keine allgemeine Aussage getroffen werden.
Beispiele für unterschiedliches Randverhalten
Die folgenden drei Beispiele haben jeweils Konvergenzradius 1:
Herleitung
Die Formeln für den Konvergenzradius lassen sich aus den Konvergenzkriterien für Reihen herleiten.
Wurzelkriterium
Die Formel von Cauchy-Hadamard ergibt sich aus dem Wurzelkriterium. Nach diesem Kriterium konvergiert die Potenzreihe
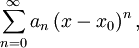
absolut wenn
![\underset{n\to \infty }{\mathop{\lim \sup }}\,\sqrt[n]{\left| a_n\left(x-x_0\right)^n \right|} = \left|x-x_0\right|\underset{n\to \infty }{\mathop{\lim \sup }}\,\sqrt[n]{|a_n|}&lt;1.](/pictures/dewiki/98/b4c029cdf81d666d899a14a25e784ac8.png)
Auflösen nach 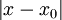 liefert den Konvergenzradius
liefert den Konvergenzradius
![\left|x-x_0\right|&lt;\frac 1{\underset{n\to \infty }{\mathop{\lim \sup }}\sqrt[n]{|a_n|}}=r.](/pictures/dewiki/51/336242c7bafe7ac4391d14534cb01166.png)
Quotientenkriterium
Die Potenzreihe 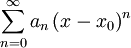 konvergiert nach dem Quotientenkriterium, wenn folgende Bedingung erfüllt ist:
konvergiert nach dem Quotientenkriterium, wenn folgende Bedingung erfüllt ist:
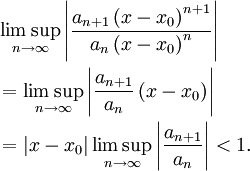
Auflösen nach 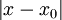 liefert den Konvergenzradius
liefert den Konvergenzradius
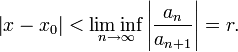
Die Potenzreihe konvergiert also für 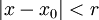 .
.
Literatur
- E. Freitag, R. Busam: Funktionentheorie. 2. Auflage. Springer-Verlag, Berlin 1995, ISBN 3-540-58650-4.
- P. Hartmann: Mathematik für Informatiker. 3. Auflage. Friedr. Vieweg & Sohn Verlag, Wiesbaden 2004, ISBN 3-528-23181-5.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Augustin Louis Cauchy — [ogysˈtɛ̃ lwi koˈʃi] (* 21. August 1789 in Paris; † 23. Mai 1857 in Sceaux) war ein französischer Ma … Deutsch Wikipedia
Liste von Mathematikern — Diese Liste bedeutender Mathematiker stellt eine Auswahl von Mathematikern von der Antike bis zu Gegenwart dar. Die Auswahl der Mathematiker richtet sich dabei nach ihren wissenschaftlichen Leistungen oder ihrem Bekanntheitsgrad, aufgrund deren… … Deutsch Wikipedia
Konvergenzradius — Als Konvergenzradius einer Potenzreihe der Form ist die größte Zahl r definiert, für welche die Potenzreihe für alle x mit | x − x0 | < r konvergiert: Dabei kennzeichnet sup das Supremum der Menge. Falls die Potenzreihe auf der ganzen… … Deutsch Wikipedia
Formale Laurentreihe — Die Laurent Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe ähnlich einer Potenzreihe, aber zusätzlich mit negativen Exponenten. Allgemein hat eine Laurent Reihe in x mit Entwicklungspunkt c diese Gestalt: Dabei sind die an und das … Deutsch Wikipedia
Laurent-Entwicklung — Die Laurent Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe ähnlich einer Potenzreihe, aber zusätzlich mit negativen Exponenten. Allgemein hat eine Laurent Reihe in x mit Entwicklungspunkt c diese Gestalt: Dabei sind die an und das … Deutsch Wikipedia
Laurent Reihe — Die Laurent Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe ähnlich einer Potenzreihe, aber zusätzlich mit negativen Exponenten. Allgemein hat eine Laurent Reihe in x mit Entwicklungspunkt c diese Gestalt: Dabei sind die an und das … Deutsch Wikipedia
Laurentreihe — Die Laurent Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe ähnlich einer Potenzreihe, aber zusätzlich mit negativen Exponenten. Allgemein hat eine Laurent Reihe in x mit Entwicklungspunkt c diese Gestalt: Dabei sind die an und das … Deutsch Wikipedia
Laurentreihen — Die Laurent Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe ähnlich einer Potenzreihe, aber zusätzlich mit negativen Exponenten. Allgemein hat eine Laurent Reihe in x mit Entwicklungspunkt c diese Gestalt: Dabei sind die an und das … Deutsch Wikipedia
Laurent-Reihe — Die Laurent Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe ähnlich einer Potenzreihe, aber zusätzlich mit negativen Exponenten. Allgemein hat eine Laurent Reihe in x mit Entwicklungspunkt c diese Gestalt: Dabei sind die an und das … Deutsch Wikipedia
Potenzreihe — Unter einer Potenzreihe versteht man in der Analysis eine unendliche Reihe der Form ist hierbei eine beliebige Folge von reellen oder komplexen Zahlen. x0 wird als der Entwicklungspunkt der Potenzreihe bezeichnet. Hinsichtlich der Konvergenz sind … Deutsch Wikipedia
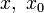 reell, so ist der Konvergenzbereich nach Auflösung der Betragsungleichung das Intervall
reell, so ist der Konvergenzbereich nach Auflösung der Betragsungleichung das Intervall 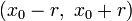 sowie möglicherweise einer der oder beide Randpunkte. Für Potenzreihen im Komplexen, das heißt, alle diese Größen können komplexe Zahlen sein, besteht der Konvergenzbereich dieser Funktionenreihe aus dem Inneren der Kreisscheibe um den Mittelpunkt x0 und mit Radius r sowie möglicherweise aus einigen Randpunkten.
sowie möglicherweise einer der oder beide Randpunkte. Für Potenzreihen im Komplexen, das heißt, alle diese Größen können komplexe Zahlen sein, besteht der Konvergenzbereich dieser Funktionenreihe aus dem Inneren der Kreisscheibe um den Mittelpunkt x0 und mit Radius r sowie möglicherweise aus einigen Randpunkten.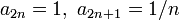 : Die zugehörige Reihe hat Konvergenzradius 1, aber der angegebene Limes existiert nicht. Die Formel von Cauchy-Hadamard ist dagegen immer anwendbar.
: Die zugehörige Reihe hat Konvergenzradius 1, aber der angegebene Limes existiert nicht. Die Formel von Cauchy-Hadamard ist dagegen immer anwendbar.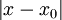 liefert den Konvergenzradius
liefert den Konvergenzradius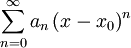 konvergiert nach dem Quotientenkriterium, wenn folgende Bedingung erfüllt ist:
konvergiert nach dem Quotientenkriterium, wenn folgende Bedingung erfüllt ist: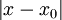 liefert den Konvergenzradius
liefert den Konvergenzradius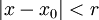 .
.
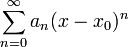
![r=\frac{1}{\limsup\limits_{n\rightarrow\infty}\left(\sqrt[n]{|a_n|}\right)}.](/pictures/dewiki/57/9026caee3746222ff14d9c7c63976d95.png)
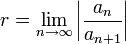
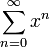
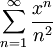
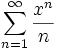
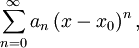
![\underset{n\to \infty }{\mathop{\lim \sup }}\,\sqrt[n]{\left| a_n\left(x-x_0\right)^n \right|} = \left|x-x_0\right|\underset{n\to \infty }{\mathop{\lim \sup }}\,\sqrt[n]{|a_n|}&lt;1.](/pictures/dewiki/98/b4c029cdf81d666d899a14a25e784ac8.png)
![\left|x-x_0\right|&lt;\frac 1{\underset{n\to \infty }{\mathop{\lim \sup }}\sqrt[n]{|a_n|}}=r.](/pictures/dewiki/51/336242c7bafe7ac4391d14534cb01166.png)