- Euklidischer Körper
-
Ein euklidischer Körper ist ein Körper (im Sinne der Algebra), der ein geordneter Körper ist und in dem jedes nichtnegative Element eine Quadratwurzel hat.
Jeder reell abgeschlossene Körper ist euklidisch und jeder euklidische Körper ist ein pythagoreischer Körper und ein formal reeller Körper.
Euklidische Körper spielen in der synthetischen Geometrie eine wichtige Rolle: Der Koordinatenkörper K einer euklidischen Ebene K2 ist stets ein euklidischer Körper, auf diesen Körpern lässt sich stets eine euklidische Ebene aufbauen. Der Begriff „Euklidische Ebene“ ist dabei etwas allgemeiner als in der üblichen Geometrie, wo die euklidische Ebene etwa durch Hilberts Axiomensystem der euklidischen Geometrie so definiert wird, dass sie zwingend eine affine Ebene über dem speziellen euklidischen Körper der reellen Zahlen ist - eine zu Hilberts System gleichwertige Formulierung in der Sprache der linearen Algebra lautet: Eine euklidische Ebene ist ein affiner Raum, dessen Vektorraum der Verschiebungen ein zweidimensionaler euklidischer Vektorraum, also isomorph zu
 mit einem Skalarprodukt ist. Die euklidischen Ebenen der synthetischen Geometrie stehen in engem Zusammenhang mit klassischen Fragen der Konstruierbarkeit. Aus diesen Fragestellungen ergeben sich zusätzliche Axiome, wie das Winkelmesseraxiom, das die Existenz eines Bogenmaßes fordert, und das Winkelteilungsaxiom, die nicht in allen euklidischen Ebenen erfüllbar sind.
mit einem Skalarprodukt ist. Die euklidischen Ebenen der synthetischen Geometrie stehen in engem Zusammenhang mit klassischen Fragen der Konstruierbarkeit. Aus diesen Fragestellungen ergeben sich zusätzliche Axiome, wie das Winkelmesseraxiom, das die Existenz eines Bogenmaßes fordert, und das Winkelteilungsaxiom, die nicht in allen euklidischen Ebenen erfüllbar sind.Eine gewisse Bedeutung haben euklidische Körper als Gegenbeispiele in der Theorie der Körpererweiterungen und der Galoistheorie, daneben bei Transzendenzuntersuchungen in der Zahlentheorie.
Euklidische Körper und Ebenen tragen ihre Namen zu Ehren des antiken Mathematikers Euklid von Alexandria, wobei beide ihren Namen seinem axiomatischen Aufbau der - bis heute nach ihm benannten - euklidischen Geometrie in seinem Werk „Die Elemente“ verdanken. → Der Begriff „Euklidischer Ring“ aus der Teilbarkeitstheorie in kommutativen Ringen steht in keinem engeren inhaltlichen Zusammenhang zu den im vorliegenden Artikel beschriebenen Begriffen als dem, dass er ebenfalls nach Euklid und zwar nach dem von ihm beschriebenen euklidischen Algorithmus benannt ist.
Inhaltsverzeichnis
Alternative Definitionen
Ein pythagoreischer Körper K, also ein Körper, in dem jede Summe von Quadraten wieder ein Quadrat ist, ist genau dann ein euklidischer Körper, wenn er genau die zwei Quadratklassen Q1 und Q − 1 enthält. Zwar ist durch diese rein algebraische Definition noch keine Anordnung gegeben, aber es gibt in solchen pythagoreischen Körpern nur genau eine Möglichkeit, sie zu einem geordneten Körper zu machen und zwar durch die Definition
- a < b genau dann, wenn b − a ein Quadrat (also ein Element von Q1) ist.
Damit kann man diese „kanonische Anordnung“ als durch die algebraische Struktur mit gegeben ansehen. In den folgenden Definitionen sollen alle Körper, die nur eine Anordnung zulassen, die dann immer diese kanonische ist, als mit dieser Anordnung ausgestattet angesehen werden.
Ein Körper K ist genau dann euklidisch wenn er
- ein geordneter pythagoreischer Körper mit genau zwei Quadratklassen,
- ein pythagoreischer Körper mit genau zwei Quadratklassen Q1 und Q − 1,
- ein formal reeller Körper mit genau zwei Quadratklassen,
- ein Körper der Charakteristik 0 mit genau zwei Quadratklassen Q1 und Q − 1 oder
- ein formal reeller Körper, der keine formal reelle, quadratische Körpererweiterung zulässt
ist.
Eigenschaften
Ein euklidischer Körper K
- hat stets die Charakteristik 0,
- enthält immer unendlich viele Elemente,
- ist nie algebraisch abgeschlossen,
- ist stets formal reell und pythagoreisch,
- enthält zu jeder reinquadratischen Gleichung
 genau zwei verschiedene Lösungen,
genau zwei verschiedene Lösungen, - kann auf genau eine Art angeordnet werden,
- ist genau dann reell abgeschlossen, wenn K(i) algebraisch abgeschlossen ist,
- besitzt als einzigen Körperautomorphismus die identische Abbildung.
Eine Verschärfung der letztgenannten Eigenschaft: Ist K < L eine Körpererweiterung und ist K ein euklidischer und L ein formal reeller Körper, dann gibt es genau eine Einbettungsabbildung von K nach L.
Und eine Folgerung der letztgenannten Eigenschaft: Eine Körpererweiterung K < L mit einem euklidischen Erweiterungskörper L ist genau dann galoissch über K, wenn K = L ist.
In geometrischen Anwendungen sind euklidische Körper meist Teilkörper der reellen Zahlen und also archimedisch angeordnet. Dass dies nicht notwendig so sein muss, zeigt das Beispiel der hyperreellen Zahlen.
Beispiele und Gegenbeispiele
Euklische Körper sind neben dem wichtigsten Beispiel, dem der reellen Zahlen
 :
:- die reellen algebraischen Zahlen
 (das sind die reellen Zahlen im algebraischen Abschluss des Körpers der rationalen Zahlen
(das sind die reellen Zahlen im algebraischen Abschluss des Körpers der rationalen Zahlen  ),
), - der Körper der hyperreellen Zahlen.
Für jede Teilmenge M von
 , die
, die  enthält, ist die Menge der aus M „mit Zirkel und Lineal konstruierbaren“ reellen Zahlen ein euklidischer Körper. Dieser Körper ist der kleinste euklidische Körper, in dem M als Teilmenge enthalten ist, und für
enthält, ist die Menge der aus M „mit Zirkel und Lineal konstruierbaren“ reellen Zahlen ein euklidischer Körper. Dieser Körper ist der kleinste euklidische Körper, in dem M als Teilmenge enthalten ist, und für  der kleinste euklidische Körper E überhaupt: Jeder euklidische Körper enthält einen zu E isomorphen Teilkörper.
der kleinste euklidische Körper E überhaupt: Jeder euklidische Körper enthält einen zu E isomorphen Teilkörper.- Der genannte kleinste euklidische Körper E besteht genau aus denjenigen reellen algebraischen Zahlen c, für die ein Turm von quadratischen Körpererweiterungen
 existiert, so dass
existiert, so dass  und
und  für ein
für ein  ist. Notwendig für die Existenz des Turms ist dabei, dass der Erweiterungsgrad der Körpererweiterung
ist. Notwendig für die Existenz des Turms ist dabei, dass der Erweiterungsgrad der Körpererweiterung  eine Potenz von 2 ist
eine Potenz von 2 ist ![\left(\left[ \Q(c):\Q\right]=2^m; m\in \N_0\right)](6/d460e7c712f1f7fc4e2734122ded1c6d.png) .
. - Der euklidische Körper der aus einer Menge M
 mit Zirkel und Lineal konstruierbaren Zahlen besteht genau aus denjenigen reellen und über
mit Zirkel und Lineal konstruierbaren Zahlen besteht genau aus denjenigen reellen und über  algebraischen Zahlen c, für die ein entsprechender Turm über
algebraischen Zahlen c, für die ein entsprechender Turm über  existiert, und der Grad von c über K0 ist dann notwendig eine Potenz von 2.
existiert, und der Grad von c über K0 ist dann notwendig eine Potenz von 2.
- Dass die beschriebenen Mengen tatsächlich Körper sind, das heißt dass mit 2 Elementen mit der angegebenen Eigenschaft auch deren Summe und Produkt etc. die geforderte Eigenschaft hat, ist am einfachsten geometrisch einzusehen. → Siehe Konstruierbare Polygone.
In allen Fällen sind die euklidischen Körper über
 unendlichdimensionale
unendlichdimensionale  -Vektorräume, das heißt Körpererweiterungen unendlichen Grades.
-Vektorräume, das heißt Körpererweiterungen unendlichen Grades. ist ein Beispiel für einen formal reellen Körper, der nicht euklidisch ist.
ist ein Beispiel für einen formal reellen Körper, der nicht euklidisch ist.- Der kleinste euklidische Körper E ist euklidisch, aber nicht reell abgeschlossen, da die Nullstellen von X3 − 2 im algebraischen Abschluss von
 alle den Grad 3 über
alle den Grad 3 über  haben und daher nicht in E liegen, damit kann auch E(i) nicht algebraisch abgeschlossen sein.
haben und daher nicht in E liegen, damit kann auch E(i) nicht algebraisch abgeschlossen sein.
Euklidische Ebenen und die euklidische Ebene
Euklidische Ebenen in der synthetischen Geometrie erfüllen alle Axiome der Axiomengruppen I bis IV in Hilberts Axiomensystem, aber nicht immer die beiden Stetigkeitsaxiome, die die Gruppe V bilden:
- V.1. (Axiom des Messens oder Archimedisches Axiom). Sind AB und CD irgendwelche Strecken, so gibt es eine Anzahl n derart, dass das n-malige Hintereinanderabtragen der Strecke CD von A aus auf den durch B gehenden Halbstrahl über den Punkt B hinausführt.
- V.2. (Axiom der (linearen) Vollständigkeit) Zu den Punkten einer Geraden können, bei Erhalt ihrer Anordnungs- und Kongruenzbeziehungen, keine weiteren Punkte hinzugefügt werden, ohne dass die unter den vorherigen Elementen bestehenden Beziehungen, die aus den Axiomen I-III folgenden Grundeigenschaften der linearen Anordnung und Kongruenz oder aber das Axiom V.1 verletzt werden.
In der Nonstandardmathematik (siehe Internal Set Theory) kann das archimedische Axiom übertragen werden: Anstelle einer endlichen Anzahl
 von Abtragungen, wird dann in der Nonstandardversion die hyperendliche Anzahl n in der inneren Menge
von Abtragungen, wird dann in der Nonstandardversion die hyperendliche Anzahl n in der inneren Menge  zugelassen. Für diese euklidischen Ebenen sind dann (bei entsprechender Übertragung aller anderen Axiome, die auf unendliche Teilmengen der Ebene oder endliche Zählmengen mit unbestimmter Anzahl Bezug nehmen) genau die reelle und die hyperreelle euklidische Ebene ein Modell. - In dieser hyperreellen euklidischen Ebene kann ein reguläres Vieleck auch eine wohlbestimmte hyperendliche Anzahl von Ecken haben. Die synthetische Standardgeometrie liefert auch über dem euklidischen Körper der hyperreellen Zahlen nicht diese Geometrie.
zugelassen. Für diese euklidischen Ebenen sind dann (bei entsprechender Übertragung aller anderen Axiome, die auf unendliche Teilmengen der Ebene oder endliche Zählmengen mit unbestimmter Anzahl Bezug nehmen) genau die reelle und die hyperreelle euklidische Ebene ein Modell. - In dieser hyperreellen euklidischen Ebene kann ein reguläres Vieleck auch eine wohlbestimmte hyperendliche Anzahl von Ecken haben. Die synthetische Standardgeometrie liefert auch über dem euklidischen Körper der hyperreellen Zahlen nicht diese Geometrie.In der Standardgeometrie werden die Axiome der Stetigkeit durch ein Axiom ersetzt, das gewährleistet, dass die Konstruktionen mit Zirkel und Lineal niemals aus dem Koordinatenbereich herausführen. Dann erfüllen genau die Ebenen über euklidischen Körpern, wie sie in diesem Artikel beschrieben sind, das neue Axiomensystem.
 zum euklidischen Anordnungsaxiom
zum euklidischen Anordnungsaxiom
Ein anderes Axiomensystem, das diese euklidischen Ebenen beschreibt, erhält man, wenn man zusätzlich zu den Axiomen einer pythagoreischen Ebene das folgende euklidische Anordnungsaxiom hinzunimmt:
- (E) Es gibt eine Anordnung "zwischen", so dass von drei verschiedenen kollinearen Punkten, A,B,D genau dann D zwischen A und B liegt, wenn sich über der Strecke AB ein bei C rechtwinkliges Dreieck ABC mit dem Höhenfußpunkt D errichten lässt.[1]
Die Anordnung "zwischen" auf Geraden der Ebene muss natürlich die anderen, von den Anordnungen auf einer pythagoreischen Ebene geforderten geometrischen Eigenschaften erfüllen, woraus dann folgt, dass sie von einer der in formal reellen pythagoreischen Körpern stets möglichen Körperanordnungen induziert wird.
Eine affine Ebene ist genau dann euklidisch (im Sinne der synthetischen Geometrie), wenn sie eine pythagoreische Ebene ist und (E) erfüllt. Jede Koordinatenebene K2 über einem euklidischen Körper wird durch die Anordnung, die von der in K einzig möglichen Körperanordnung induziert wird, und durch die (bis auf Koordinatentransformation) einzig mögliche Orthogonalität zu einer solchen euklidischen Ebene. Jede euklidische Ebene ist isomorph zu einer solchen Koordinatenebene über einem euklidischen Körper.
Bedeutung des Euklidischen Anordnungsaxioms
Seiner Form nach fordert das Euklidische Anordnungsaxiom nur, dass die Anordnung der Ebene, deren Existenz das Axiom fordert, mit der auf der pythagoreischen Ebene definierten Orthogonalitätsrelation verträglich sei. Es ist bemerkenswert, dass diese "anschaulich selbstverständliche" Verträglichkeitsforderung impliziert, dass überhaupt nur eine Anordnung der Ebene möglich ist und dass die Ebene unter Konstruktionen mit Zirkel und Lineal abgeschlossen ist. [2]
- Eine "stark" angeordnete, pappussche Ebene ist immer isomorph zu einer Koordinatenebene über einem geordneten Körper. Solche Körper enthalten immer wenigstens die zwei Quadratklassen Q1 und Q − 1. Daher kann auf der Ebene stets eine Orthogonalitätsrelation definiert werden. (→Präeuklidische Ebene).
- Die Orthogonalitätsrelation muss für eine pythagoreische Ebene so beschaffen sein, dass jeder Winkel der Ebene halbiert werden kann (die Ebene muss frei beweglich sein), also speziell jeder rechte Winkel, woraus die Existenz von Quadraten folgt und damit, dass die Orthogonalitätskonstante quadratisch äquivalent zu − 1 ist. (→Präeuklidische Ebene#Quadrate).
- Gerade unter diesen Voraussetzungen existieren noch unendlich viele verträgliche Orthogonalitätsrelationen: Wählt man ein festes Bezugssystem (O,E1,E2), dann liefert jede Zahl c < 0 im geordneten Körper als Orthogonalitätskonstante (bezogen auf dieses Koordinatensystem) eine andere Orthogonalitätsrelation! Jede dieser Orthogonalitätsrelationen führt in einer euklidischen Ebene aber, wenn man (E) zur Definition der Anordnung verwendet, zur gleichen Anordnung der Ebene.
Motivation
Die Beispiele für euklidische Körper machen deutlich, wodurch die Verallgemeinerung der reellen ebenen Geometrie motiviert ist: Die euklidischen Ebenen spiegeln wieder, welche Konstruktionen bei bestimmten Vorgaben der Menge M möglich sind. Figuren, die sich aus M nicht mit Zirkel und Lineal konstruieren lassen, sind in der aus M konstruierten euklidischen Ebene einfach nicht vorhanden! Während der reelle Abschluss von
 sozusagen der größte über
sozusagen der größte über  algebraische Körper ist, auf dem eine euklidische Ebene (im Sinn der synthetischen Geometrie) aufgebaut werden kann, die die „Vorgabelängen“ enthält, sind die in den Beispielen genannten euklidischen Körper die kleinsten Körper mit diesen Eigenschaften.
algebraische Körper ist, auf dem eine euklidische Ebene (im Sinn der synthetischen Geometrie) aufgebaut werden kann, die die „Vorgabelängen“ enthält, sind die in den Beispielen genannten euklidischen Körper die kleinsten Körper mit diesen Eigenschaften.Archimedische euklidische Ebene
Eine euklidische Ebene ist genau dann archimedisch angeordnet (kurz: archimedisch), erfüllt also das Axiom V.1 des Messens, wenn ihr Koordinatenkörper ein archimedischer (kurz für: archimedisch geordneter) Körper ist. Dies ist offensichtlich genau dann der Fall, wenn dieser euklidische Körper K zu einem Teilkörper der reellen Zahlen isomorph ist. In diesem Fall gibt es – aufgrund der algebraisch eindeutig bestimmten Anordnung von K − genau eine Einbettung
 und der Körper kann stets mit dem „reellen Modell“
und der Körper kann stets mit dem „reellen Modell“  identifiziert werden.
identifiziert werden.Ein „kleines“ und geometrisch allenfalls für Gegenbeispiele interessantes Modell eines nicht archimedischen euklidischen Körpers erhält man, wenn man den rationalen Funktionenkörper in einer Variablen
 analog zu der oben für
analog zu der oben für  beschriebenen Konstruktion innerhalb seines algebraischen Abschlusses reellquadratisch abschließt.
beschriebenen Konstruktion innerhalb seines algebraischen Abschlusses reellquadratisch abschließt.Analytische Geometrie auf euklidischen Ebenen
In der analytischen Geometrie werden unter anderem
- Normalformen für die affinen Selbstabbildungen eines affinen Raumes, speziell die Affinitäten auf diesem Raum,
- Normalformen für quadratische Formen und die zugehörigen Quadriken
bestimmt. In beiden Aspekten verhält sich die euklidische Ebene über einem archimedischen euklidischen Körper K, der hier mit seinem „reellen Modell“ identifiziert wird, im Wesentlichen wie die affine bzw. euklidische Ebene über
 , denn ausschlaggebend ist hier die Existenz (oder Nichtexistenz) von Eigenwerten zu
, denn ausschlaggebend ist hier die Existenz (oder Nichtexistenz) von Eigenwerten zu  -Matrizen mit Einträgen aus K. Eigenwerte, die hier die Nullstellen eines charakteristischen Polynoms vom Grad 2 sind, existieren für solche Matrizen genau dann in K, wenn sie in
-Matrizen mit Einträgen aus K. Eigenwerte, die hier die Nullstellen eines charakteristischen Polynoms vom Grad 2 sind, existieren für solche Matrizen genau dann in K, wenn sie in  existieren! Jede
existieren! Jede  -Matrix mit Einträgen aus K, die reell diagonalisierbar ist, ist auch über K diagonalisierbar, hat sie eine jordansche Normalform über
-Matrix mit Einträgen aus K, die reell diagonalisierbar ist, ist auch über K diagonalisierbar, hat sie eine jordansche Normalform über  , dann ist sie auch über K zu dieser jordanschen Normalform ähnlich.
, dann ist sie auch über K zu dieser jordanschen Normalform ähnlich.Besonders für quadratische Formen und Quadriken ist bedeutsam, dass eine symmetrische
 -Matrix mit Einträgen aus K durch eine Orthogonalmatrix mit Einträgen aus K diagonalisiert werden kann. Die Eigenwerte dieser euklidischen Normalform sind dann entweder 0 oder quadratisch äquivalent zu −1 oder 1. Daher existieren in der euklidischen Ebene über K ebenso viele affine Äquivalenzklassen von Quadriken, wie über der reellen Koordinatenebene. (→ Siehe Hauptachsentransformation)
-Matrix mit Einträgen aus K durch eine Orthogonalmatrix mit Einträgen aus K diagonalisiert werden kann. Die Eigenwerte dieser euklidischen Normalform sind dann entweder 0 oder quadratisch äquivalent zu −1 oder 1. Daher existieren in der euklidischen Ebene über K ebenso viele affine Äquivalenzklassen von Quadriken, wie über der reellen Koordinatenebene. (→ Siehe Hauptachsentransformation)Dies stimmt im allgemeinen nur im zweidimensionalen affinen Raum über K, also in der Ebene.
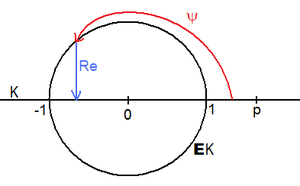
Ebenen mit Bogenmaß
Für eine übersichtliche Darstellung wird ein euklidischer Körper K im folgenden als Teilkörper von
 aufgefasst, auch wenn analoge Konstruktionen auch für nicht archimedische euklidische Ebenen und Körper möglich sind. Die hier dargestellte Einführung eines Bogenmaßes bedeutet, dass auf einer Ebene, aus der Konstruktionen mit Zirkel und Lineal nicht herausführen, die also eine euklidische Ebene ist, ein zusätzliches Konstruktionswerkzeug „Winkelmesser“ eingeführt wird, mit dem es möglich ist, Bogenlängen (Winkelmaße) auf Strecken „abzuwickeln“.
aufgefasst, auch wenn analoge Konstruktionen auch für nicht archimedische euklidische Ebenen und Körper möglich sind. Die hier dargestellte Einführung eines Bogenmaßes bedeutet, dass auf einer Ebene, aus der Konstruktionen mit Zirkel und Lineal nicht herausführen, die also eine euklidische Ebene ist, ein zusätzliches Konstruktionswerkzeug „Winkelmesser“ eingeführt wird, mit dem es möglich ist, Bogenlängen (Winkelmaße) auf Strecken „abzuwickeln“.Dazu wird die orientierte euklidische Ebene A über K mit der Zahlenebene
 identifiziert. Die Orientierung von A und damit
identifiziert. Die Orientierung von A und damit  hat den technischen Zweck, dass die Identifizierung von
hat den technischen Zweck, dass die Identifizierung von  mit
mit  im richtigen Drehsinn erfolgt, so dass Drehungen im mathematisch positiven Sinn das richtige Vorzeichen erhalten. Eine Drehung wα der Punktebene
im richtigen Drehsinn erfolgt, so dass Drehungen im mathematisch positiven Sinn das richtige Vorzeichen erhalten. Eine Drehung wα der Punktebene  um den Ursprung kann dann durch die Multiplikation mit einer komplexen Zahl z = eiα dargestellt werden:
um den Ursprung kann dann durch die Multiplikation mit einer komplexen Zahl z = eiα dargestellt werden: .
.
Damit entspricht jede Drehung wα der reellen Ebene um den Ursprung umkehrbar eindeutig einer Zahl eiα = a + ib auf dem komplexen Einheitskreis
 . Dieser Einheitskreis ist zugleich als Untergruppe von
. Dieser Einheitskreis ist zugleich als Untergruppe von  isomorph zur Gruppe
isomorph zur Gruppe  der Drehungen um den Ursprung und α liefert für die Drehung wα um den Winkel α und damit für jeden orientierten Winkel ein (orientiertes) Bogenmaß (ein orientiertes Winkelmaß im üblichen Sinn) α, das bis auf die Addition von Vielfachen des Vollwinkelmaßes 2π eindeutig ist.
der Drehungen um den Ursprung und α liefert für die Drehung wα um den Winkel α und damit für jeden orientierten Winkel ein (orientiertes) Bogenmaß (ein orientiertes Winkelmaß im üblichen Sinn) α, das bis auf die Addition von Vielfachen des Vollwinkelmaßes 2π eindeutig ist.Die Gruppe der Drehungen der euklidischen Ebene
 um den Ursprung ist isomorph zu der Untergruppe
um den Ursprung ist isomorph zu der Untergruppe 
Man definiert: Ein surjektiver Homomorphismus

- mit der Eigenschaft, dass ein Element
 existiert, so dass der Realteil
existiert, so dass der Realteil  das Intervall
das Intervall ![[0,p]\cap K](4/fb49f011bd0b6e9d6043c8339c08af5b.png) bijektiv und streng monoton fallend auf das Intervall
bijektiv und streng monoton fallend auf das Intervall ![[-1,1]\cap K](4/7b45c605fd66505efe1a50a383a98aa9.png) abbildet und
abbildet und  ist, wird ein Bogenmaß auf der euklidischen Ebene A genannt. Die Zahl p heißt die Kreiszahl des Bogenmaßes.
ist, wird ein Bogenmaß auf der euklidischen Ebene A genannt. Die Zahl p heißt die Kreiszahl des Bogenmaßes.
Natürlich können bei jeder Koordinatenebene über einem Teilkörper von
 die Drehungen und Winkel durch reelle Maßzahlen beschrieben werden. Das Entscheidende ist hier, dass jeder Klasse von gleichlangen Strecken mit der Länge l in der euklidischen Ebene, wobei
die Drehungen und Winkel durch reelle Maßzahlen beschrieben werden. Das Entscheidende ist hier, dass jeder Klasse von gleichlangen Strecken mit der Länge l in der euklidischen Ebene, wobei  ist, durch das Bogenmaß umkehrbar eindeutig eine Drehung der Ebene ψ(l) entspricht und die Addition von Zahlen, das heißt das Hintereinanderabtragen solcher Strecken mit der Komposition der zugehörigen Drehungen übereinstimmt!
ist, durch das Bogenmaß umkehrbar eindeutig eine Drehung der Ebene ψ(l) entspricht und die Addition von Zahlen, das heißt das Hintereinanderabtragen solcher Strecken mit der Komposition der zugehörigen Drehungen übereinstimmt!Die Existenz eines Bogenmaßes ist ein zusätzliches Axiom in der synthetischen Geometrie für euklidische Ebenen, es wird auch als Winkelmesseraxiom[3] bezeichnet. Seine Gültigkeit ist unabhängig von den übrigen Axiomen, die kleinste euklidische Ebene besitzt kein Bogenmaß, ebenso wenig die Ebene über dem Körper
 der reellen algebraischen Zahlen.[4].
der reellen algebraischen Zahlen.[4].In einer orientierten, archimedisch angeordneten euklidischen Ebene mit Bogenmaß gibt es zu jeder Zahl
 genau ein Bogenmaß, das p als Kreiszahl hat. Dieses Bogenmaß bestimmt ein orientiertes Winkelmaß, das heißt für zwei Drehungen ψ(l1),ψ(l2) ist
genau ein Bogenmaß, das p als Kreiszahl hat. Dieses Bogenmaß bestimmt ein orientiertes Winkelmaß, das heißt für zwei Drehungen ψ(l1),ψ(l2) ist  genau dann, wenn sie gleich (für " + ") bzw. invers zueinander (für " − ") sind.
genau dann, wenn sie gleich (für " + ") bzw. invers zueinander (für " − ") sind.In der orientierten Ebene
 sind genau die Homomorphismen
sind genau die Homomorphismen  Bogenmaße im Sinne der synthetischen Geometrie, ihre Kreiszahl ist dann p = π / c.
Bogenmaße im Sinne der synthetischen Geometrie, ihre Kreiszahl ist dann p = π / c.In einer euklidischen Ebene mit Bogenmaß
- existiert zu jeder natürlichen Zahl
 ein regelmäßiges n-Eck,
ein regelmäßiges n-Eck, - gibt es zu jeder Drehung wα und jeder natürlichen Zahl
 eine Drehung wα / n mit
eine Drehung wα / n mit  .
.
Die zweite Aussage, die gelegentlich als Winkelteilungsaxiom bezeichnet wird, impliziert die erste. Beide Eigenschaften hat die kleinste euklidische Ebene nicht, während die euklidische Ebene über den reellen algebraischen Zahlen beide erfüllt. Sie sind also keine hinreichenden Bedingungen für die Existenz eines Bogenmaßes.
Hinreichend für die Existenz eines Bogenmaßes ist, dass die Einschränkungen der Winkelfunktionen cos und sin auf den euklidischen Körper K nur Bilder in K haben. Mit dieser Beobachtung lässt sich ein (als Menge) abzählbarer euklidischer Körper konstruieren, dessen Koordinatenebene ein Bogenmaß besitzt.[5]
Literatur
- Wendelin Degen und Lothar Profke: Grundlagen der affinen und euklidischen Geometrie, Teubner, Stuttgart, 1976, ISBN 3-519-02751-8
- Hans Freudenthal: Mathematik als pädagogische Aufgabe 1. Stuttgart 1973
- Thomas W. Hungerford: Algebra. 5. print. Springer-Verlag, 1989, ISBN 0-387-90518-9
- Theodor Schneider: Einführung in die transzendenten Zahlen. Berlin-Göttingen-Heidelberg 1957
- Bartel Leendert van der Waerden: Algebra 1. 8. Auflage, Berlin-Heidelberg-New York 1971
Einzelnachweise
Wikimedia Foundation.