- Endliche einfache Gruppe
-
Endliche einfache Gruppen, im Folgenden kurz als einfache Gruppen bezeichnet, gelten in der Gruppentheorie (einem Teilgebiet der Mathematik) als die Bausteine der endlichen Gruppen.
Einfache Gruppen spielen für die endlichen Gruppen eine ähnliche Rolle wie die Primzahlen für die natürlichen Zahlen: Jede endliche Gruppe lässt sich in endlich vielen Schritten aus einfachen Gruppen konstruieren; jede endliche Gruppe lässt sich auch wieder in ihre einfachen Gruppen zerteilen. Es gibt jedoch keine „noch einfacheren Gruppen“, aus denen sich die endlichen einfachen Gruppen konstruieren lassen.
Inhaltsverzeichnis
Definition
Eine endliche Gruppe E mit mindestens zwei Elementen ist eine einfache Gruppe, wenn für jeden surjektiven Gruppenhomomorphismus
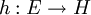 eine der beiden folgenden Bedingungen gilt:
eine der beiden folgenden Bedingungen gilt:- Die Abbildung h ist injektiv (und daher bijektiv), d. h. die Gruppen E und H sind gleich mächtig.
- Die Abbildung ist trivial, h bildet alle Elemente von E auf das neutrale Element e von H ab.
Jeder nichttriviale Homomorphismus einer einfachen Gruppe ist also ein Isomorphismus. Eine hierzu äquivalente Definition ist, dass die Gruppe E genau dann einfach ist, wenn sie nur {e} und sich selbst als Normalteiler besitzt.
Klassifikation
Seit 1962 war bekannt, dass alle nicht-abelschen einfachen Gruppen eine gerade Ordnung haben müssen (Satz von Feit und Thompson). Bis zur vollständigen Klassifikation war es aber noch ein weiter Weg.
Seit 1982 sind die endlichen einfachen Gruppen vollständig klassifiziert:
- Die abelschen Gruppen von Primzahlordnung
- Die Gruppen vom Lie-Typ, 16 jeweils unendliche Serien
- Die alternierenden Gruppen
- Die 26 sporadischen Gruppen
Zum Beweis des Klassifikationssatzes
Die Herleitung des Satzes war eines der umfangreichsten Projekte der Mathematikgeschichte:
- Der Beweis verteilt sich auf über 500 Fachartikel mit zusammen fast 15.000 gedruckten Seiten. Es sind aber nicht alle Beweise auch publiziert worden.
- Über 100 Mathematiker waren von Ende der 1920er bis Anfang der 1980er Jahre daran beteiligt.
Da Teile des Satzes mit Hilfe von Computern überprüft wurden, wird der Beweis jedoch nicht von allen Mathematikern anerkannt. Nach der „Fertigstellung“ des Beweises um 1980 ist von führenden Mathematikern des Klassifikationsprogramms wie Michael Aschbacher und Daniel Gorenstein ein Programm gestartet worden, den Beweis zu vereinfachen und lückenlos zu dokumentieren. Dabei sind auch Lücken entdeckt worden, von denen die meisten ohne größere Komplikationen geschlossen werden konnten; eine Lücke erwies sich allerdings als so hartnäckig, dass erst 2002 durch Aschbacher und andere ein Beweis erbracht werden konnte (Aschbacher, Smith: The classification of quasithin groups, AMS), der immerhin 1200 Seiten lang war - ein Grund war allerdings, dass sich die Autoren bemühten, diesmal möglichst ohne Verweise auszukommen.
Familien einfacher Gruppen (Beispiele)
Zyklische Gruppen mit Primzahlordnung
Die zyklischen Gruppen Zp mit p = 2, 3, 5, 7, 11,... bilden eine Familie einfacher Gruppen.
Bei den einfachen Gruppen fallen die Eigenschaften zyklisch und kommutativ zusammen, denn jede zyklische Gruppe ist kommutativ und jede einfache kommutative Gruppe ist zyklisch.
Bei den einfachen Gruppen fallen die Eigenschaften zyklisch und ungerade Ordnung beinahe zusammen:
- Jede einfache zyklische Gruppe - außer Z2 - besitzt eine ungerade Anzahl von Elementen.
- Jede einfache Gruppe mit ungerader Ordnung gehört zu den zyklischen Gruppen.
Alternierende Permutationsgruppen
Die alternierenden Permutationsgruppen Altn mit n größer als 4 bilden eine Familie der einfachen Gruppen.
Sporadische Gruppen
Die ersten 5 der insgesamt 26 sporadischen Gruppen (siehe dort zu einer tabellarischen Übersicht) wurden von Émile Mathieu bereits in den Jahren 1862 und 1873 entdeckt.
Die 21 „jüngeren“ Gruppen wurden ab 1964 gefunden; meist erfolgte die Entdeckung im Rahmen der Beweissuche zum Klassifikationssatz. Da diese Gruppen zum Teil recht groß sind, vergingen zwischen ihrer gruppentheoretischen Entdeckung und dem praktischen Beweis ihrer Existenz oft mehrere Jahre. Die größte aller 26 sporadischen Gruppen, die sogenannte Monstergruppe F1 mit rund 8 × 1053 Elementen, wurde bereits 1973 von Bernd Fischer und Robert Griess junior entdeckt, ihre endgültige Konstruktion gelang Griess jedoch erst 1980.
Von einigen Autoren wird auch die Gruppe 2F4(2)' mit 17971200 = 211·33·52·13 Elementen zu den sporadischen Gruppen gezählt, womit sich eine Gesamtzahl von 27 ergibt.
Weblinks und Literatur
- Die Klassifikation der endlichen einfachen Gruppen (PDF, 131 KB)
- Die sporadischen Gruppen (PostScript, 460 KB)
- Classification Theorem of Finite Groups
- Aschbacher The Status of the classification of the finite simple groups, Notices AMS 2004, pdf, englisch
- Daniel Gorenstein: Die Klassifikation der endlichen einfachen Gruppen in…
- der Zeitschrift Spektrum der Wissenschaft, Februar 1986
- und dem Sammelband Moderne Mathematik, Heidelberg 1996, ISBN 3-8274-0025-2
- Gorenstein, Lyons, Solomon: The classification of the finite simple groups, 1994, AMS Books online, englisch, Bd.2 von 1996 ist hier: [1]
Siehe auch
Wikimedia Foundation.
