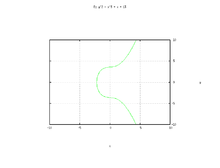
- Elliptic Curve Cryptography
-
Unter Elliptic Curve Cryptography (ECC) oder deutsch Elliptische-Kurven-Kryptographie versteht man asymmetrische Kryptosysteme, die Operationen auf elliptischen Kurven über endlichen Körpern verwenden. Die Sicherheit dieser Verfahren basiert auf der Schwierigkeit der Berechnung des diskreten Logarithmus in der Gruppe der Punkte der elliptischen Kurve.
Jedes Verfahren, das auf dem diskreten Logarithmus in endlichen Körpern basiert, wie z. B. der Digital Signature Algorithm, das Elgamal-Kryptosystem oder der Diffie-Hellman-Schlüsselaustausch, lässt sich in einfacher Weise auf elliptische Kurven übertragen und somit zu einem Elliptic Curve Cryptosystem umformen. Dabei werden die beim Originalverfahren eingesetzten Operationen (Multiplikation und Exponentiation) auf dem endlichen Körper durch entsprechende Operationen (Punktaddition und Punktmultiplikation) der Punkte auf der elliptischen Kurve ersetzt. Das n-fache Addieren eines Punktes P mit sich selbst (also die Multiplikation mit dem Skalar n) wird mit nP bezeichnet und entspricht einer Exponentiation xn im ursprünglichen Verfahren.
Das Prinzip wurde Mitte der 1980er Jahre von Victor S. Miller und Neal Koblitz unabhängig voneinander vorgeschlagen.
Inhaltsverzeichnis
Funktionsprinzip
Der Austausch eines gemeinsamen geheimen Schlüssels ist mit dem Diffie-Hellman-Schlüsselaustausch auf Basis elliptischer Kurven (kurz ECDH) möglich.[1] Dieses Verfahren ist hier als Beispiel für Kryptographie auf Basis elliptischer Kurven angegeben:
Bestimmung der Schlüssel
Beide Seiten A und B des zu sichernden Kommunikationskanals einigen sich öffentlich auf eine gültige elliptische Kurve und einen Punkt P auf dieser Kurve. Weiter beschafft A sich geheim eine Zufallszahl as, diese Zahl ist der private Schlüssel von A. Analog beschafft sich B seinen privaten Schlüssel bs.
Nun berechnet A seinen öffentlichen Schlüssel, den Punkt Ap = asP. Analog bestimmt B seinen öffentlichen Schlüssel Bp = bsP. Da die Punkte auf der elliptischen Kurve zusammen mit einem „unendlichen Punkt“ eine Gruppe bilden, liegen beide öffentliche Schlüssel auf der Kurve.
Ver- und Entschlüsseln
Es gilt nun asBp = asbsP = bsasP = bsAp. Damit ist ein Punkt der Kurve gegeben, der nur für A und B einfach zu berechnen ist und für alle anderen zufällig aussieht. Er stellt daher ein öffentlich ausgetauschtes Geheimnis dar und kann als Schlüssel verwendet werden. Analog zum Diffie-Hellman-Schlüsselaustausch beruht die Sicherheit auf dem Decisional-Diffie-Hellman-Problem in der verwendeten elliptischen Kurve. Dieses Problem ist verwandt mit dem Diskreter-Logarithmus-Problem, aus den öffentlichen Punkten P und Ap oder P und Bp die Zufallszahlen as beziehungsweise bs zu berechnen. Dies ist bisher für geeignet gewählte Kurvenparameter nicht gelungen und gilt daher als ein schwieriges Problem.
Effizienz
Da das Problem des diskreten Logarithmus in elliptischen Kurven deutlich schwerer ist als die Berechnung des diskreten Logarithmus in endlichen Körpern oder die Faktorisierung ganzer Zahlen, kommen Kryptosysteme, die auf elliptischen Kurven beruhen – bei vergleichbarer Sicherheit – mit erheblich kürzeren Schlüsseln aus als die herkömmlichen asymmetrischen Kryptoverfahren, wie z. B. das RSA-Kryptosystem oder der Diffie-Hellman-Schlüsselaustausch. Die derzeit schnellsten Algorithmen sind der Babystep-Giantstep-Algorithmus und die Pollard-Rho-Methode, deren Laufzeit bei
 liegt, wobei n die Bitlänge der Größe des zugrundeliegenden Körpers ist. Nach heutigem Kenntnisstand wird z. B. mit einer Schlüssellänge von 160 Bit eine ähnliche Sicherheit erreicht wie bei RSA mit 1024 Bit.[2]
liegt, wobei n die Bitlänge der Größe des zugrundeliegenden Körpers ist. Nach heutigem Kenntnisstand wird z. B. mit einer Schlüssellänge von 160 Bit eine ähnliche Sicherheit erreicht wie bei RSA mit 1024 Bit.[2]ECC eignet sich daher besonders dann, wenn die Speicher- oder Rechenkapazität begrenzt ist, z. B. in Smartcards.
Vergleich der Verschlüsselungsstärken[3] Symmetric Key Size (bits) RSA and Diffie-Hellman Key Size (bits) Elliptic Curve Key Size (bits) 80 1024 160 112 2048 224 128 3072 256 192 7680 384 256 15360 521 Vergleich des Berechnungsaufwands[3] Security Level (bits) Ratio of DH Cost : EC Cost 80 3:1 112 6:1 128 10:1 192 32:1 256 64:1 Die mathematischen Operationen auf elliptischen Kurven sind aufwändiger zu berechnen als Operationen in vergleichbar großen endlichen Körpern oder RSA-Modulen. Wegen der erheblich kürzeren Schlüssel können Kryptosysteme, die auf elliptischen Kurven beruhen, bei vergleichbarem Sicherheitniveau trotzdem schneller sein als die gleichen Verfahren auf Basis des diskreten Logarithmus in einem endlichen Körper oder als RSA.[4] Ein Vergleich der Recheneffizienz dieser kryptographischen Verfahren hängt jedoch stark von den Details der Implementierung (kryptographische Parameter, Arithmetik, Optimierungen, Programmiersprache und Compiler, zugrunde liegende Hardware) ab.
Bekannte Verfahren
- Elliptic Curve Diffie-Hellman (ECDH)
- Elliptic Curve Integrated Encryption Scheme (ECIES), auch Integrated Encryption Scheme (IES) genannt
- Elliptic Curve Digital Signature Algorithm (ECDSA)
- ECMQV, ein von Menezes, Qu und Vanstone vorgeschlagenes Protokoll zur Schlüsselvereinbarung
Angriffe auf Implementierungen
Timingangriff
Im Mai 2011 veröffentlichten die Forscher Billy Bob Brumley und Nicola Tuveri ein Paper, [5] in welchem sie einen erfolgreichen Timingangriff auf ECDSA beschreiben. [6] Dabei setzten die Forscher einen Server mit OpenSSL auf. Der Angriff erfolgte über die Tatsache, dass das Ver- und Entschlüsseln mit unterschiedlichen ECDSA Schlüsseln unterschiedlich viel Zeit in Anspruch nimmt. So konnten Brumley und Tuveri ohne Zugriff auf den Server den privaten Schlüssel berechnen.
Verwendung
Elliptic Curve Cryptographie wird von modernen Windows-Betriebssystemen (ab Vista) unterstützt.[7]
Produkte der Mozilla Foundation (u.a. Firefox, Thunderbird) unterstützen ECC mit min. 256 Bit Key-Länge (P-256 aufwärts).[8]
Die in Österreich gängigen Bürgerkarten (e-card, Bankomat- oder a-sign Premium Karte) verwenden ECC seit ihrer Einführung 2004/2005, womit Österreich zu den Vorreitern in deren breitem Einsatz zählt.[9]
Die Reisepässe der meisten Europäischen Staaten (u. a. Deutschland) verwenden ECC zumindest für den Schutz des Zugriffs auf den Chip mittels Extended Access Control, einige Länder (u. a. Deutschland und Schweiz) verwenden es auch, um die auf dem Chip gespeicherten Daten mit Passive Authentication zu schützen.[10]
In Deutschland verwendet der neue Personalausweis ebenfalls ECC, sowohl für Extended Access Control als auch für Passive Authentication.[11]
Sony benutzt ECC zur digitalen Signierung von Software für die PlayStation 3. Im Jahr 2010 gelang einer Hackergruppe die Ermittlung des benutzten Private Key und somit ein fast vollständiger Bruch der Sicherheitssysteme. Dies war jedoch vor allem auf Implementationsfehler von Sony zurückzuführen und nutzte keine Sicherheitslücken in ECC-Verfahren aus.[12]
Patente
Laut NSA sind Implementierungen mit Patentproblemen konfrontiert. Vor allem die kanadische Certicom Inc. besitzt demnach mehr als 130 Patente, die für ECC oder Public-Key-Kryptographie benötigt werden. 26 davon wurden von der NSA lizenziert um ECC-Verfahren zu Zwecken nationaler Sicherheit zu implementieren.[3]
In einer Studie der A-SIT wird auf Patente in effizienten Implementierungen hingewiesen, wobei ECC selbst "prinzipiell patentfrei" sei. [13]
Standardisierungsgremien und Normen
ANSI
ANSI X9.62-2005 ist die aktuelle Standardisierung des ECDSA.[14]
- ANSI X9.62
- ANSI X9.63
NIST
- FIPS 186-2
- FIPS 186-3 [15]
IPSEC
ISO
- ISO 14888-3 [16]
- ISO 15946 [17]
IEEE
- IEEE 1363 [18]
SECG
Die "Standards for Efficient Cryptography Group" (SECG) ist ein 1998 gegründetes Konsortium zur Förderung des Einsatzes von ECC-Algorithmen.[19]
Siehe auch
Weblinks
- Video einer Vorlesung von Neal Koblitz über Elliptic-Curve-Cryptology, 1998, MPG - 1,8GB (englisch)
- ECC-Arbeitsgruppe, Domainparameter
- Tutorial mit Java Applets - Krypto-Verfahren basierend auf elliptischen Kurven
- Freie Implementation des "Elliptic Curve DSA" für Windows und Linux, Download und Anleitung(englisch)
Einzelnachweise
- ↑ Victor S. Miller: Use of Elliptic Curves in Cryptography. In: Advances in Cryptology. 218, 1986.
- ↑ Cryptographic Key Length Recommendation. BlueKrypt, abgerufen am 3. November 2011 (englisch).
- ↑ a b c The Case for Elliptic Curve Cryptography. 15. Januar 2009, abgerufen am 3. November 2011 (englisch).
- ↑ R. Szerwinski und T. Güneysu: Exploiting the Power of GPUs for Asymmetric Cryptography. Proceedings of CHES 2008, pp. 79-99, 2008
- ↑ Billy Bob Brumley, Nicola Tuveri: Remote Timing Attacks are Still Practical. In: Cryptology ePrint Archive: Report 2011/232. 11. Mai 2011, abgerufen am 3. November 2011 (englisch, Abruf als PDF möglich).
- ↑ Erfolgreiche Timing-Angriffe auf Verschlüsselung mit elliptischen Kurven. heise.de, 23. Mai 2011, abgerufen am 3. November 2011 (deutsch).
- ↑ Elisabeth Oswald: Kryptosysteme basierend auf Elliptischen Kurven Einsatz und Verbreitung in Standardsoftware. Zentrum für sichere Informationstechnologie - Austria (A-SIT), 29. Juli 2009, abgerufen am 2. November 2011 (PDF, deutsch).
- ↑ Mozilla CA Certificate Maintenance Policy (Version 2.0). mozilla.org, 4. November 2011, abgerufen am 4. November 2011 (englisch): „We consider the following algorithms and key sizes to be acceptable and supported in Mozilla products: ... Elliptic Curve Digital Signature Algorithm (using ANSI X9.62) over SECG and NIST named curves P-256, P-384, and P-512;“
- ↑ Elliptische Kurven. Abgerufen am 3. November 2011 (deutsch).
- ↑ Zdeněk Říha: Electronic passports. JRC Ispra, European Commission, Masaryk University, Brno, 13. September 2008, abgerufen am 3. November 2011 (PDF, englisch).
- ↑ Dr. Manfred Lochter und Dr. Johannes Merkle: Ein neuer Standard für elliptische Kurven. 2009, abgerufen am 3. November 2011 (PDF, deutsch, Vortrag vom 11. Deutschen IT-Sicherheitskongress 2009).
- ↑ 27C3: Sicherheitssystem der Playstation 3 ausgehebelt. heise.de, 30. Dezember 2010, abgerufen am 5. November 2011.
- ↑ Elisabeth Oswald: Einsatz und Bedeutung Elliptischer Kurven für die elektronische Signatur. A-SIT, 2011, S. 27, abgerufen am 2. November 2011 (PDF, deutsch).
- ↑ ANSI X9.62-2005, Public Key Cryptography for the Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA)
- ↑ Digital Signature Standard (DSS). FIPS PUB 186-3. National Institute of Standards and Technology (NIST), 2009, abgerufen am 3. November 2011 (PDF, englisch).
- ↑ Information technology -- Security techniques -- Digital signatures with appendix -- Part 3: Discrete logarithm based mechanisms. ISO/IEC, abgerufen am 3. November 2011 (englisch, Kostenpflichtiger PDF-Abruf): „ISO/IEC 14888-3:2006 specifies digital signature mechanisms with appendix whose security is based on the discrete logarithm problem. It provides a general description of a digital signature with appendix mechanism, and a variety of mechanisms that provide digital signatures with appendix.“
- ↑ Information technology -- Security techniques -- Cryptographic techniques based on elliptic curves. ISO/IEC, abgerufen am 3. November 2011 (englisch, Kostenpflichtiger PDF-Abruf): „ISO/IEC 15946 specifies public-key cryptographic techniques based on elliptic curves. It consists of five parts and includes the establishment of keys for symmetric cryptographic techniques, and digital signature mechanisms.“
- ↑ Standard Specifications For Public-Key Cryptography. The IEEE P1363 project develops Standard Specifications For Public-Key Cryptography, towards the goal of issuing a series of IEEE standards documents.. IEEE, 10. Oktober 2008, abgerufen am 3. November 2011 (englisch).
- ↑ http://www.secg.org/index.php?action=secg,about
Kategorie:- Kryptologisches Verfahren
Wikimedia Foundation.