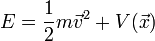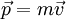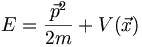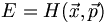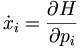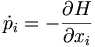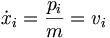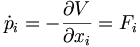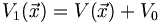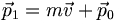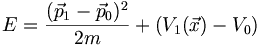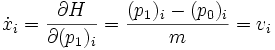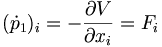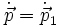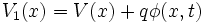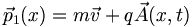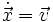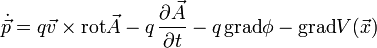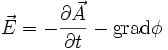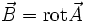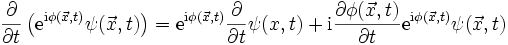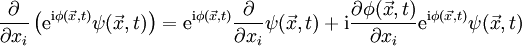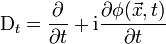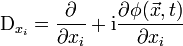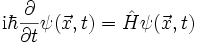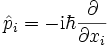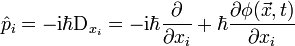Eichinvarianz

Unter einer Eichtheorie versteht man eine Feldtheorie, die einer lokalen Eichsymmetrie genügt.

Anschaulich bedeutet dies, dass die von der Theorie vorhergesagten Wechselwirkungen sich nicht ändern, wenn eine bestimmte Größe lokal frei gewählt wird. Diese Möglichkeit, eine Größe an jedem Ort unabhängig festzulegen – zu eichen wie einen Maßstab – veranlasste den deutsch-amerikanischen Mathematiker Hermann Weyl in den 1920er Jahren zur Wahl des Namens Eichinvarianz bzw. Eichsymmetrie.

Weyl entdeckte die Eichinvarianz zunächst in der Elektrodynamik und versuchte durch Anwendung des Prinzips auf Einsteins allgemeine Relativitätstheorie die Elektrodynamik und die Gravitation zu einer Theorie zu vereinigen. Die daraus resultierende Theorie erwies sich jedoch als falsch.

Eichtheorien in der Physik der Elementarteilchen

Die moderne Teilchenphysik ist bestrebt das Verhalten der elementaren Teilchen aus möglichst einfachen ersten Prinzipien abzuleiten. Ein nützliches Hilfsmittel ist dabei die Forderung nach einer Gruppe von Transformationen (z. B. Rotationen) der beteiligten Felder, unter der die Dynamik der Teilchen invariant bleibt. Diese Symmetrie oder Eichfreiheit schränkt die Gestalt der zu konstruierenden Lagrangedichte enorm ein und hilft so bei der Konstruktion der gesuchten Theorie.

Allgemein lässt sich in einer Eichtheorie eine kovariante Ableitung definieren, aus dieser ein Feldstärketensor konstruieren und somit eine Lagrangedichte und Wirkung, aus der sich per Variation die Bewegungsgleichungen und Erhaltungsgrößen ergeben.

Das Standardmodell der Elementarteilchenphysik enthält zwei solcher Eichtheorien: die Theorie der starken Wechselwirkung mit der Symmetriegruppe SU(3)_C, und die Theorie der elektroschwachen Wechselwirkung mit der Symmetriegruppe $SU(2)_I \times U(1)_Y$.

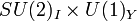Das Noether-Theorem garantiert, dass jedem Teilchen, das der zu beschreibenden Wechselwirkung unterliegt, eindeutig eine erhaltene Ladung zugeordnet werden kann; z. B. elektrische Ladung e, Hyperladung Y, schwacher Isospin I₃, Color C. Diese Ladung gibt an wie stark ein Teilchen an die Eichbosonen koppelt, sowie das Vorzeichen dieser Kopplung (z. B. anziehend/abstoßend im elektromagnetischen Fall).

Eichtheorie am Beispiel der Elektrodynamik

Eichsymmetrie der Bewegungsgleichung von Punktteilchen

Die Energie eines Teilchens in einem äußeren statischen Potenzial lässt sich schreiben als

$E = \frac{1}{2}m\vec v^2 + V(\vec x)$

mit vorgegebenem Potenzial $V(\vec x)$.

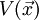Definiert man nun den Impuls als

$\vec p = m \vec v$

so kann man die Energie auch schreiben als

$E = \frac{\vec p^2}{2m} + V(\vec x)$

Wenn man nach der Hamiltonschen Mechanik die Energie als Funktion von Ort und Impuls beschreibt, also

$E = H(\vec x,\vec p)$

dann erhält man aus deren Ableitungen die Bewegungsgleichungen:

$\dot x_i = \frac{\partial H}{\partial p_i}$

$\dot p_i = -\frac{\partial H}{\partial x_i}$

Für die oben genannte Energie ergibt das

$\dot x_i = \frac{p_i}{m} = v_i$

$\dot p_i = -\frac{\partial V}{\partial x_i} = F_i$

Wenn man zum Potenzial und zum Impuls jeweils noch einen konstanten Term hinzufügt, also definiert:

$V_1(\vec x) = V(\vec x) + V_0$

$\vec p_1 = m\vec v + \vec p_0$

und dann die Bewegung des Teilchens mittels der „Index-1-Größen“ beschreibt, dann lautet die Energie

$E = \frac{(\vec p_1 - \vec p_0)^2}{2m} + (V_1(\vec x) - V_0)$

und die Bewegungsgleichungen sind

$\dot x_i = \frac{\partial H}{\partial (p_1)_i} = \frac{(p_1)_i - (p_0)_i}{m} = v_i$

$(\dot p_1)_i = -\frac{\partial V}{\partial x_i} = F_i$

Da außerdem

$\dot{\vec p} = \dot{\vec p}_1$

(denn Konstanten verschwinden ja in der Ableitung), sind das genau dieselben Bewegungsgleichungen.

Es ist also möglich, sowohl für die Energie als auch für den Impuls einen konstanten Summanden festzulegen, ohne die dadurch beschriebene Physik zu verändern. Diese Eigenschaft nennt man globale Eichsymmetrie.

Nun stellt sich die Frage, ob man stattdessen auch nicht-konstante Größen aufaddieren kann, ohne die Bewegungsgleichungen zu verändern, also allgemein

$V_1(x) = V(x) + q\phi(x, t)\,$

$\vec p_1(x) = m\vec v + q\vec A(x, t)$

wobei die Konstante q herausgezogen wurde, weil es sich nachher als praktisch erweisen wird; für die Argumentation hat diese Tatsache aber keine Bedeutung.

Es ist unmittelbar klar, dass es nicht möglich ist, beliebige Funktionen für φ und 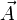$\vec A$ zu verwenden, da z. B. ein beliebiges φ wie ein zusätzliches Potenzial wirkt. Nimmt man für beide Größen beliebige Funktionen an, so zeigt Nachrechnen, dass die Bewegungsgleichungen gegeben sind durch

$\dot{\vec x} = \vec v$

$\dot{\vec p} = q\vec v\times\operatorname{rot} \vec A - q\,\frac{\partial\vec A}{\partial t} - q\,\operatorname{grad} \phi -\operatorname{grad} V(\vec{x})$

Dies sind aber gerade die Bewegungsgleichungen, die man erwarten würde, wenn das Teilchen die Ladung q hat und sich außer im Potenzial auch noch im elektrischen Feld

$\vec E = - \frac{\partial\vec A}{\partial t} - \operatorname{grad} \phi$

und im magnetischen Feld

$\vec B = \operatorname{rot} \vec A$

bewegt.

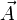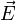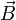Die Bewegung wird nun nicht geändert, wenn die Änderung von φ und $\vec A$ nicht die Felder $\vec E$ und $\vec B$ ändert (also insbesondere die Felder auf null lässt, wenn sie vorher null waren). Da die Rotation eines Gradientenfeldes stets null ist, ist klar, dass durch die Addition des Gradienten einer beliebigen orts- und zeitabhängigen skalaren Funktion zum Vektorpotenzial 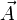$\vec A$ nichts am magnetischen Feld geändert wird. Allerdings ändert dies das elektrische Feld um die Zeitableitung eben dieses Gradienten; diese Änderung kann jedoch kompensiert werden, indem das skalare Potenzial φ um die Zeitableitung derselben Funktion verringert wird.

Eichsymmetrie der quantenmechanischen Wellenfunktion

In der Quantenmechanik werden Teilchen nicht mehr durch Ort und Impuls, sondern durch die sogenannte Wellenfunktion 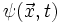$\psi(\vec x,t)$ beschrieben. Diese ist ein Feld, also eine Funktion von Raum und Zeit, und im Allgemeinen komplex (z. B. ist sie in der nichtrelativistischen Schrödingergleichung ein komplexer Skalar und in der Dirac-Gleichung ein komplexer Spinor). 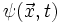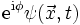Allerdings ist sie nicht eindeutig: Die Wellenfunktionen $\psi(\vec x,t)$ und $\mathrm{e}^{\mathrm{i}\phi}\psi(\vec x,t)$ mit beliebig gewähltem 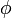$\!\,\phi$ beschreiben beide denselben Zustand. Hierbei handelt es sich wiederum um eine globale Symmetrie. Mathematisch wird diese Symmetrie durch die Liegruppe U(1) beschrieben.

Wie vorher im Fall der klassischen Bewegungsgleichung stellt sich hier die Frage, ob man statt der globalen Phase auch eine orts- und zeitabhängige Phase einführen könnte. Nun treten jedoch in der Bewegungsgleichung der Wellenfunktion (Schrödingergleichung, Dirac-Gleichung etc.) partielle Ableitungen auf, die bei der so veränderten Wellenfunktion zu Zusatztermen führen:

$\frac{\partial}{\partial t}\left(\mathrm{e}^{\mathrm{i}\phi(\vec x,t)}\psi(\vec x,t)\right) = \mathrm{e}^{\mathrm{i}\phi(\vec x,t)}\frac{\partial}{\partial t}\psi(x,t) + \mathrm{i}\frac{\partial\phi(\vec x,t)}{\partial t}\mathrm{e}^{\mathrm{i}\phi(\vec x,t)}\psi(\vec x,t)$

$\frac{\partial}{\partial x_i}\left(\mathrm{e}^{\mathrm{i}\phi(\vec x,t)}\psi(\vec x,t)\right) = \mathrm{e}^{\mathrm{i}\phi(\vec x,t)}\frac{\partial}{\partial x_i}\psi(\vec x,t) + \mathrm{i}\frac{\partial\phi(\vec x,t)}{\partial x_i}\mathrm{e}^{\mathrm{i}\phi(\vec x,t)}\psi(\vec x,t)$

Diese Beziehungen kann man auch so interpretieren, dass die partiellen Orts- und Zeitableitungen durch die Ableitungsoperatoren

$\operatorname{D}_t = \frac{\partial}{\partial t} + \mathrm{i}\frac{\partial\phi(\vec x,t)}{\partial t}$

$\operatorname{D}_{x_i} = \frac{\partial}{\partial x_i} + \mathrm{i}\frac{\partial\phi(\vec x,t)}{\partial x_i}$

ersetzt werden. Der Zusammenhang mit dem elektromagnetischen Feld erschließt sich, wenn man die Form der Schrödingergleichung betrachtet:

$\mathrm{i}\hbar\frac{\partial}{\partial t}\psi(\vec x, t) = \hat H\psi(\vec x, t)$

wobei im Hamilton-Operator 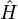$\hat H$ die Ortsableitungen über die Komponenten des Impulsoperators

$\hat p_i = -\mathrm{i}\hbar\frac{\partial}{\partial x_i}$

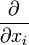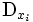auftreten. Ersetzen wir im Impulsoperator nun $\frac{\partial}{\partial x_i}$ durch $\operatorname{D}_{x_i}$, so erhalten wir

$\hat p_i = -\mathrm{i}\hbar \operatorname{D}_{x_i} = -\mathrm{i}\hbar\frac{\partial}{\partial x_i} + \hbar\frac{\partial\phi(\vec x,t)}{\partial x_i}$

Es tritt also ein zusätzlicher Summand auf, der wie ein Beitrag zum elektromagnetischen Vektorpotential 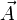$\vec A$ aussieht. Analog ergibt sich beim Einsetzen von 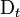$\operatorname{D}_t$ in die Schrödingergleichung ein zusätzlicher Potentialterm der Form 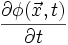$\frac{\partial\phi(\vec x,t)}{\partial t}$. Diese zusätzlichen elektromagnetischen Potentiale erfüllen aber gerade die Eichbedingung für elektromagnetische Felder, so dass die Physik in der Tat durch die lokale Phase nicht beeinflusst wird, sondern nur in der Beschreibung die elektromagnetischen Potentiale angepasst werden müssen.

Im Zusammenhang mit Beziehungen der Art 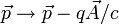$\vec p \to \vec p-q\vec A/c$ redet man oft von „minimal subtraction“.

Eichtheorien in der Mathematik

In der Mathematik spielen Eichtheorien ebenfalls eine bedeutende Rolle bei der Klassifikation 4-dimensionaler Mannigfaltigkeiten. So konnten Edward Witten und Nathan Seiberg 1994 mit eichtheoretischen Methoden topologische Invarianten definieren.

Siehe auch

Nichtabelsche Eichtheorien werden im Artikel Yang-Mills-Theorie behandelt.

Literatur

• Dietmar Ebert: Eichtheorien – Grundlage der Elementarteilchenphysik. VCH-Verlag, Weinheim 1989, ISBN 3-527-27819-2.
• David Bailin, Alexander Love: Introduction to gauge field theory. Inst. of Physics Publ., Bristol 1994, ISBN 0-7503-0281-X.
• Ta-Pei Cheng, Ling-Fong Li: Gauge theory of elementary particle physics. Oxford Univ. Press, Oxford 2006, ISBN 0-19-851961-3.