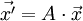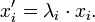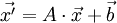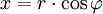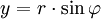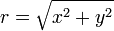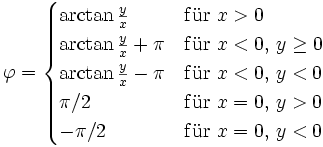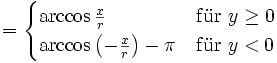Affine Transformation

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Bei einer Koordinatentransformation werden Koordinaten von einem Koordinatensystem in ein anderes übertragen. Formal gesehen ist dies der Übergang von den ursprünglichen Koordinaten (x₁,x₂,...,x_N) zu den neuen Koordinaten (x'₁,x'₂,...,x'_N).

Typische Transformationsvorgänge sind: Verschiebung (Translation), Drehung (Rotation) und Veränderung des Maßstabs (Skalierung).

Die x'_i können beliebige Funktionen aller x_i sein. In der Regel verwendet man spezielle Transformationen, bei denen diese Funktionen gewissen Einschränkungen, z. B. Differenzierbarkeit oder Linearität, unterliegen.

Koordinatentransformationen können angewendet werden, wenn sich ein Problem in einem anderen Koordinatensystem leichter lösen lässt, z. B. bei der Transformation von kartesischen Koordinaten in Kugelkoordinaten oder umgekehrt.

Lineare Transformationen

Bei linearen Transformationen sind die neuen Koordinaten lineare Funktionen der ursprünglichen, also

x'₁ = a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n

x'₂ = a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n

usw.

bzw.

$\vec{x'}=A\cdot\vec{x}$

Der Ursprung des neuen Koordinatensystems stimmt dabei mit dem des alten überein.

Verschiebung (Translation)

Verschiebung

Eine Translation kann entweder als Verschiebung des Koordinatenursprungs oder (leichter vorstellbar) als Verschiebung der abgebildeten Objekte gedeutet werden.

Im 2D-Raum erfordert eine Translation zwei Parameter: Verschiebung in x-Richtung (tx) und in y-Richtung (ty).
Analog dazu gibt es in 3D drei Parameter: zusätzliche Verschiebung in z-Richtung (tz).

Beispiel

Wir betrachten zwei Koordinatensysteme S und S'. S ist gegenüber S' um den Vektor 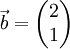$\vec{b} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}$ verschoben.

Ein Punkt P, der im Koordinatensystem S die Koordinaten 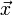$\vec{x}$ hat, besitzt dann im Koordinatensystem S' die Koordinaten $\vec{x'}=\vec{x}-\vec{b}$.

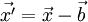Drehung (Rotation)

Drehung gegen den Uhrzeigersinn

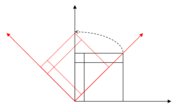
Bei einer Rotation wird das Koordinatensystem gedreht. Auch dieser Vorgang ist als Drehung der abgebildeten Objekte einfacher vorstellbar.

In zwei Dimensionen gibt es nur einen Rotationswinkel als Parameter. Im 3D-Raum kann man um alle drei Koordinatenachsen drehen. Dargestellt wird eine Drehung durch eine Drehmatrix.

Beispiel

Wir betrachten zwei (hier: dreidimensionale) kartesische Koordinatensysteme S und S' mit einer gemeinsamen z-Achse und gemeinsamen Ursprung. S' sei gegenüber S um den Winkel 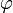$\varphi$ um die z-Achse gedreht. Ein Punkt P, der im Koordinatensystem S die Koordinaten 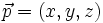$\vec p=(x, y, z)$ hat, besitzt dann im Koordinatensystem S' die Koordinaten:

• $x'=x\cos\varphi - y\sin\varphi$,
• $y'=x\sin\varphi+y\cos\varphi$,
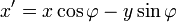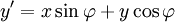• z' = z

Somit ergibt sich mit der Drehmatrix für eine Rotation des Koordinatensystems im Uhrzeigersinn (und damit des Punktes gegen den Uhrzeigersinn) $\mathbf{\begin{pmatrix} \cos\varphi & -\sin\varphi & 0 \\ \sin\varphi & \cos\varphi & 0 \\ 0 & 0 & 1\end{pmatrix}} \vec p = \vec p'$.

Skalierung

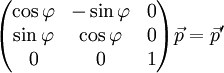Skalierung

Bei der Skalierung werden die „Einheiten“ der Achsen geändert. Das heißt, die Zahlenwerte der Koordinaten x_i werden mit konstanten Faktoren λ_i multipliziert („skaliert“)

$x_i'=\lambda_i\cdot x_i.$

Die Parameter dieser Transformation sind die N Zahlen λ_i. Ein Spezialfall ist die „Maßstabsänderung“, bei der alle Faktoren den gleichen Wert haben

λ_i = λ.

Die Skalierung ist ein Spezialfall der linearen Transformation, bei der alle Koordinatenwerte mit dem gleichen Faktor s multipliziert werden. Die Matrix A ist in diesem Fall s mal die Einheitsmatrix.

Scherung

Scherung

Bei der Scherung verändert sich der Winkel zwischen den Koordinatenachsen.

Im 2D-Raum gibt es daher einen Parameter und im 3D-Raum drei Parameter.

Affine Transformationen

Affine Transformationen bestehen aus einer oder mehreren einfachen Transformationen.

Sind beide beteiligten Koordinatensysteme linear, (d.h. im Prinzip durch einen Koordinatenursprung und gleichmäßig unterteilte Koordinatenachsen gegeben), so liegt eine affine Transformation vor. Hierbei sind die neuen Koordinaten affine Funktionen der ursprünglichen, also

x'₁ = a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n + b₁

x'₂ = a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n + b₂

usw.

Dies kann man kompakt als Matrixmultiplikation des alten Koordinatenvektors 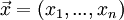$\vec{x}=(x_1,...,x_n)$ mit der Matrix A, die die Koeffizienten a_ij enthält, und Addition eines Vektors 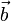$\vec{b}$, der die b_i enthält, darstellen

$\vec{x'}=A\cdot\vec{x} + \vec{b}$

Die Translation ist ein Spezialfall einer affinen Transformation, bei der A die Einheitsmatrix ist.

Beispiele

Kartesische Koordinaten und Polarkoordinaten

Hauptartikel: Polarkoordinaten

Ein Punkt in der Ebene wird im kartesischen Koordinatensystem durch seine Koordinaten (x,y) und im Polarkoordinatensystem durch den Abstand r vom Ursprung und dem (positivem) Winkel 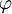${} \varphi$ zur x-Achse bestimmt.

Dabei gilt für die Umrechnung von Polarkoordinaten in kartesische Koordinaten:

• $x=r\cdot\cos\varphi$
• $y=r\cdot\sin\varphi$

Für die Umrechnung von kartesischen Koordinaten in Polarkoordinaten gilt:

• $r=\sqrt{x^2+y^2}$
• $\varphi = \begin{cases}\arctan\frac yx&\mathrm{f\ddot ur}\ x>0\\ \arctan\frac yx+\pi&\mathrm{f\ddot ur}\ x<0,\,y\geq0\\ \arctan\frac yx-\pi&\mathrm{f\ddot ur}\ x<0,\,y<0\\ \pi/2&\mathrm{f\ddot ur}\ x=0,\,y>0\\ -\pi/2&\mathrm{f\ddot ur}\ x=0,\,y<0 \end{cases}$

${}=\begin{cases}\arccos\frac xr&\mathrm{f\ddot ur}\ y\geq0\\ \arccos\left(-\frac xr\right)-\pi&\mathrm{f\ddot ur}\ y<0 \end{cases}$

Weitere Anwendungen

In der Physik sind die Galilei-Transformation und die Lorentz-Transformation wichtig.

In den Geowissenschaften - insbesondere der Geodäsie und Kartographie gibt es noch weitere Transformationen, die formal Koordinatentransformationen darstellen.

• Transformation von geographischer Breite und Länge in Gauß-Krüger-Koordinaten
• Die Umrechnungen zwischen astronomischen Koordinaten
• 7-Parameter-Transformation (Verschiebung, Drehung, Maßstab zwischen zwei Koordinatensystemen auf demselben oder anderen Referenzellipsoid(en), auch Helmert-Transformation ("Dreh-Streckung").

Im Bereich Robotik gilt die Denavit-Hartenberg-Transformation als das Standardverfahren.

Literatur

• I.N. Bronstein, K.A. Semendjajew, G. Musiol, Taschenbuch der Mathematik, Verlag Harry Deutsch, Thun, 2005, ISBN 9783817120062
• Siegfried Heitz, Koordinaten auf geodätischen Bezugsflächen, Dümmler, Bonn 1985, ISBN 3-427-78981-0
• Siegfried Heitz, Mechanik fester Körper, Band 1: Grundlagen, Dynamik starrer Körper, Dümmler, Bonn 1980, ISBN 3-427-78921-7

Weblinks

• Transformation von Koordinaten und Höhen in der Landesvermessung
• Freies Programm für ebene und räumliche Transformationen
• WTRANS Software zur Berechnung der Parameter für 2D/3D-Koordinatentransformationen für kartesische Koordianten und geographische Koordinaten (Molodenski-Ansatz), Projektionen, Geodätische Hauptaufgaben