- Deltaeder
-
Ein Deltaeder ist ein Polyeder, das ausschließlich durch gleichseitige Dreiecke begrenzt ist.
Es existieren 8 konvexe Deltaeder. Durch Zusammensetzen zweier Deltaeder lassen sich beliebig viele weitere Deltaeder erzeugen, die jedoch im Allgemeinen nicht konvex sind und deren bekanntester Repräsentant das Sterntetraeder ist.
Inhaltsverzeichnis
Konvexe Deltaeder
Deltaeder Abbildung Flächen (F) Ecken (E) Kanten (K) Tetraeder 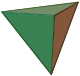
4 4 6 triangulare Bipyramide 
6 5 9 Oktaeder 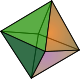
8 6 12 pentagonale Bipyramide 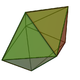
10 7 15 Trigondodekaeder 
12 8 18 dreifach erweitertes Dreiecksprisma 
14 9 21 zweifach erweitertes Antiprisma 
16 10 24 Ikosaeder 
20 12 30 Da jede Fläche an drei Kanten und umgekehrt jede Kante an zwei Flächen stößt, gilt bei einem Deltaeder garantiert immer 3F = 2K. Aus dem eulerschen Polyedersatz E+F−K = 2 ergeben sich dann weiter durch Eliminieren von K bzw. F die Formeln F = 2(E−2) sowie K = 3(E−2). Da aufgrund der Konvexität an jede Ecke maximal fünf Flächen stoßen, umgekehrt aber jede Fläche drei Ecken hat, gilt auf jeden Fall 5E ≥ 3F, woraus sich zusammen mit F = 2(E−2) die Ungleichung E ≤ 12 (folglich F ≤ 20 und K ≤ 30) ergibt.
Drei der acht existierenden konvexen Deltaedern sind platonische Körper (nämlich Tetraeder, Oktaeder und Ikosaeder). Die restlichen fünf Deltaeder sind Johnson-Körper.
Formal könnte man das einfache gleichseitige Dreieck mit zwei Seiten, drei Ecken und drei Kanten auch als Deltaeder auffassen, nur fehlt dem gleichseitigen Dreieck die Eigenschaft eines Körpers. Ausgehend vom gleichseitigen Dreieck wird jedes Deltaeder durch Hinzufügen von einer Ecke und drei Kanten zum Vorgänger erweitert. Dies lässt sich anschaulich mit einem Set aus Kugeln und Magnetstäben nachvollziehen. Allerdings wird dieses Schema einmal durchbrochen. Es ist nämlich nicht möglich, einen konvexen 18-Flächner aus gleichseitigen Dreiecken zu bauen.
14-Flächner
Der 14-Flächner ist wie folgt aufgebaut: Man nimmt ein regelmäßiges Prisma, dessen Grundfläche aus einem gleichseitigen Dreieck besteht und dessen drei Seitenflächen Quadrate sind. Auf diese drei Quadrate setze man nun je eine Pyramide mit quadratischer Grundfläche, deren Seitenflächen gleichseitige Dreiecke sind, die in der Größe identisch mit dem gleichseitigen Dreiecken der Grundfläche des Prisma sind.
16-Flächner
Der 16-Flächner ist wie folgt aufgebaut: Man nimmt ein regelmäßiges Antiprisma, dessen Grundfläche aus einem Quadrat besteht und dessen acht Seitenflächen gleichseitige Dreiecke sind. Auf die beiden quadratischen Grundflächen setze man nun je eine Pyramide mit quadratischer Grundfläche, deren Seitenflächen gleichseitige Dreiecke sind, die in der Größe identisch mit den gleichseitigen Dreiecken der Seiten des Antiprismas sind.
Nicht konvexe Deltaeder
Zu den nicht konvexen Deltaedern zählen u.a. das Boot, das kumulierte Tetraeder, das kumulierte Hexaeder und das Sterntetraeder.
Weblinks
Wikimedia Foundation.
