- Abzählende Kombinatorik
-
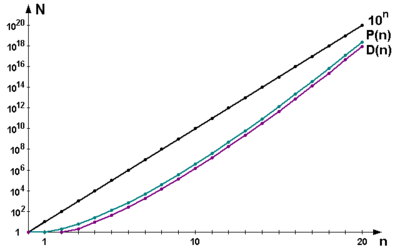 Zahl der Permutationen und Derangements (totalen Versetzungen) von n Elementen. P(n) - n-Permutationen; D(n) - totale Derangements (bei der alle n Elemente ihre Plätze wechseln)
Zahl der Permutationen und Derangements (totalen Versetzungen) von n Elementen. P(n) - n-Permutationen; D(n) - totale Derangements (bei der alle n Elemente ihre Plätze wechseln)
 Zahl der Variationen und Kombinationen von 10 Elementen zur k-ten Klasse mit und ohne Wiederholung sowie der partiellen Derangements (teilweisen Versetzungen) von 10 Elementen. P*(10;k) - k-Permutationen oder Variationen mit Wiederholung; P(10;k) - k-Permutationen oder Variationen ohne Wiederholung; D(10;10-k) - partielle Derangements (bei denen nur k der 10 Elemente die Plätze wechseln); K*(10;k) - k-Kombinationen mit Wiederholung; K(10;k) - k-Kombinationen ohne Wiederholung.
Zahl der Variationen und Kombinationen von 10 Elementen zur k-ten Klasse mit und ohne Wiederholung sowie der partiellen Derangements (teilweisen Versetzungen) von 10 Elementen. P*(10;k) - k-Permutationen oder Variationen mit Wiederholung; P(10;k) - k-Permutationen oder Variationen ohne Wiederholung; D(10;10-k) - partielle Derangements (bei denen nur k der 10 Elemente die Plätze wechseln); K*(10;k) - k-Kombinationen mit Wiederholung; K(10;k) - k-Kombinationen ohne Wiederholung.
Die abzählende Kombinatorik ist ein Teilbereich der Kombinatorik, der sich mit der Bestimmung der Anzahl möglicher Anordnungen oder Auswahlen
- unterscheidbarer oder nicht unterscheidbarer Objekte (d.h. „ohne“ bzw. „mit“ Wiederholung derselben Objekte) sowie
- mit oder ohne Beachtung ihrer Reihenfolge (d.h. geordnet“ bzw. „ungeordnet“)
beschäftigt. In der modernen Kombinatorik werden diese Auswahlen oder Anordnungen auch als Abbildungen betrachtet, so dass sich die Aufgabe der Kombinatorik in diesem Zusammenhang im Wesentlichen darauf beschränken kann, diese Abbildungen zu zählen.
Für das Rechnen mit Wahrscheinlichkeiten auf der Basis des Wahrscheinlichkeitsbegriffs von Laplace bildet die Kombinatorik eine wichtige Grundlage.
Ein verblüffendes Phänomen der Kombinatorik ist, dass sich oftmals wenige Objekte auf vielfältige Weise kombinieren lassen. Beim Zauberwürfel können beispielsweise die 26 Elemente auf rund 43 Trillionen Arten kombiniert werden. Dieses Phänomen wird oft als kombinatorische Explosion bezeichnet und ist auch die Ursache für das so genannte Geburtstagsparadoxon.
Inhaltsverzeichnis
Begriffsabgrenzungen
Aufgrund der Vielfalt der Herangehensweisen sind die Schreibweisen und Begrifflichkeiten im Bereich der Kombinatorik leider oft recht uneinheitlich. So bezeichnen übereinstimmend alle Autoren die Vertauschung der Reihenfolge einer Menge von n unterscheidbaren Elementen als Permutation (lateinisch Vertauschung). Wählt man dagegen von diesen n Elementen nur k < n Elemente aus, deren Reihenfolge man anschließend vertauscht, bezeichnen viele Autoren das nun als Variation, geordnete Stichprobe bzw. Kombination mit Berücksichtigung der Reihenfolge, andere dagegen (namentlich im englischsprachigen Raum) weiter als Permutation. Lässt man schließlich in einer solchen Auswahl von Elementen deren Reihenfolge außer Acht, wird solch eine Auswahl nun für gewöhnlich ungeordnete Stichprobe, Kombination ohne Berücksichtigung der Reihenfolge oder einfach nur Kombination (lateinisch Zusammenstellung) genannt. Kombinationen sind, sofern nichts weiter zu ihnen gesagt wird, also i.d.R. ungeordnet, Permutationen und/oder Variationen dagegen geordnet, wobei die Frage, ob man Permutationen als Sonderfälle von Variationen (oder umgekehrt) betrachtet, ggf. von Autor zu Autor unterschiedlich beantwortet wird.
Alles in allem gibt es also zunächst einmal 3 (oder auch nur 2) verschiedene Fragestellungen, die ihrerseits noch einmal danach unterteilt werden, ob es unter den ausgewählten Elementen auch Wiederholungen gleicher Elemente geben darf oder nicht. Ist ersteres der Fall, spricht man von Kombinationen, Variationen bzw. Permutationen mit Wiederholung, andernfalls solchen ohne Wiederholung. Stellt man sich schließlich vor, dass die ausgewählten Elemente dabei einer Urne o.ä. entnommen werden, wird dementsprechend auch von Stichproben mit oder ohne Zurücklegen gesprochen:
Ohne Wiederholung bzw. Zurücklegen Mit Wiederholung bzw. Zurücklegen Ohne Berücksichtigung der Reihenfolge
und k < nKombination / Ungeordnete Stichprobe
(englisch k-combination)Kombination / Ungeordnete Stichprobe Mit Berücksichtigung der Reihenfolge
und k < nVariation / Geordnete Stichprobe
(englisch k-permutation)Variation / Geordnete Stichprobe Mit Berücksichtigung der Reihenfolge
und k = nPermutation
(englisch n-permutation)Permutation Anordnungen (Permutationen)
Permutation: „Jede mögliche Anordnung von n Elementen, in der alle Elemente verwendet werden, heißt Permutation dieser Elemente.“
Permutationen von einzeln unterscheidbaren Objekten
Als einführendes Beispiel mag die Zahl der Anordnungen von sechs unterscheidbaren Objekten mit Beachtung der Reihenfolge dienen. Offensichtlich kann jedes der Objekte „auf den ersten Platz gelangen“, es gibt also sechs Möglichkeiten, den ersten Platz zu besetzen. Wenn der erste Platz besetzt ist, bleiben noch fünf Kandidaten für den zweiten Platz, ist auch dieser besetzt, nur noch vier Kandidaten für den dritten Platz, und so fort. Für den vorletzten Platz bleiben schließlich nur noch zwei Objekte übrig, und der letzte Platz muss mit dem übrig gebliebenen Objekt besetzt werden. Es gibt also
 mögliche Anordnungen.
mögliche Anordnungen.Allgemein gilt: Die Anzahl der Permutationen von n verschiedenen Elementen ist
 . Das Ausrufezeichen steht für „Fakultät“ und wird auch so gelesen, also „n Fakultät“.
. Das Ausrufezeichen steht für „Fakultät“ und wird auch so gelesen, also „n Fakultät“.- Beispiel
- Es gibt 32! Möglichkeiten, die 32 Spielkarten eines Skatblattes anzuordnen (263.130.836.933.693.530.167.218.012.160.000.000).
Die Anzahl der fixpunktfreien Permutationen (Derangements), bei denen kein Objekt auf seinem Platz bleibt, ist die Subfakultät !n. Bei sechs Objekten sind das !6 = 265 Möglichkeiten. Weiterhin lassen sich Permutationen einteilen nach der Anzahl der Zykel, aus denen sie bestehen. Die Zahl der Permutationen von n Objekten, die aus genau k Zykel bestehen, ist gegeben durch die Stirling-Zahlen erster Art.
Permutationen von klassenweise äquivalenten Objekten
Für die Zahl der möglichen Anordnungen von Objekten aus mehreren Klassen, die untereinander jeweils innerhalb einer Klasse nicht unterscheidbar sind, ist es hilfreich, zunächst die mögliche Zahl der Anordnungen der Objekte zu betrachten und dann zu überlegen, wie viele dieser Anordnungen nicht unterscheidbar sind. Die Zahl der möglichen Anordnungen bei unterscheidbaren Objekten wird durch die Zahl der nicht unterscheidbaren Anordnungen geteilt.
Wenn die mögliche Zahl von Anordnungen von zwei Objekten einer ersten Klasse, drei Objekten einer zweiten Klasse und fünf Objekten einer dritten Klasse ermittelt werden soll, dann gibt es zunächst (2 + 3 + 5)! oder 3.628.800 mögliche Anordnungen. Weil aber Anordnungen nicht unterscheidbar sind, bei denen nur Objekte einer Klasse untereinander den Platz getauscht haben, weil also jeweils
 oder 1.440 der möglichen Anordnungen gleich erscheinen, gibt es nur
oder 1.440 der möglichen Anordnungen gleich erscheinen, gibt es nur  unterscheidbare Anordnungen dieser Elemente.
unterscheidbare Anordnungen dieser Elemente.- Allgemein
Anzahl der Permutationen von n Elementen, die in k Gruppen von je
 gleichen Elementen mit
gleichen Elementen mit  fallen:
fallen:  .
.- Beispiel
- Aus dem Wort „Banane“ lassen sich insgesamt
 „Wörter“ (Anagramme) bilden.
„Wörter“ (Anagramme) bilden. - Aus je 2 verschiedenen Rot- und Blautönen lassen sich insgesamt 24 verschiedene Muster zusammenstellen. Bleichen die verschiedenen Rot- und Blautöne nun z.B. mit der Zeit aus, so dass sie am Ende nicht mehr voneinander unterscheidbar sind, bleiben damit (siehe nebenstehende Abb. rechts) nur noch 12 bzw. 6 unterscheidbare Farbmuster übrig. Erwiese sich schließlich allein das Dunkelrot als lichtecht, während alle drei übrigen Farben komplett verblassen, wären es gerade einmal 4 (Abb. links).
Auswahlen mit Beachtung der Reihenfolge (Variationen)
Variation ohne Zurücklegen
Bei der Variation ohne Zurücklegen sollen k von n Objekte (mit
 ) auf k verfügbare Plätze platziert werden, wobei jedes Objekt nur höchstens einen Platz einnehmen darf. Es gibt für den ersten Platz n mögliche Objekte, für den zweiten Platz n − 1 Objekte usw. bis zum k-ten Platz, für den es noch n − k + 1 mögliche Objekte gibt. Insgesamt gibt es also
) auf k verfügbare Plätze platziert werden, wobei jedes Objekt nur höchstens einen Platz einnehmen darf. Es gibt für den ersten Platz n mögliche Objekte, für den zweiten Platz n − 1 Objekte usw. bis zum k-ten Platz, für den es noch n − k + 1 mögliche Objekte gibt. Insgesamt gibt es alsomögliche Anordnungen. Für diese Zahl existieren auch die Notationen
 und (n)k, die als fallende Faktorielle bezeichnet werden.
und (n)k, die als fallende Faktorielle bezeichnet werden.- Mengendarstellung
- Die Menge
 ist die Menge aller Variationen ohne Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Variationen ohne Wiederholung von n Dingen zur Klasse k (für  ). Sie heißt auch Menge aller Permutationen ohne Wiederholung von n Dingen zur Klasse k und hat die oben angegebene Anzahl von Elementen.
). Sie heißt auch Menge aller Permutationen ohne Wiederholung von n Dingen zur Klasse k und hat die oben angegebene Anzahl von Elementen.
- Beispiel
- Wenn aus 8 Objekten 3 mal ohne Zurücklegen gezogen wird, sind 8·7·6 verschiedene Auswahlen möglich: bei der ersten Ziehung noch 8 Möglichkeiten, dann nur noch 7 und für die dritte Ziehung schließlich nur noch 6 Möglichkeiten.
- Sollen von 8 Objekten alle 8 ausgewählt werden, ergibt sich dementsprechend eine Zahl von insgesamt 8·7·6·…·1 = 8! Möglichkeiten, also die Zahl der Permutationen aller 8 Elemente.
Variation mit Zurücklegen
Wenn aus n Objekten k Objekte mit Beachtung ihrer Reihenfolge und mit Zurücklegen ausgewählt werden sollen, kann jedes der n Objekte auf jedem der k Plätze der Auswahl erscheinen, und es gibt demzufolge nk mögliche Auswahlen.
- Mengendarstellung
- Die Menge
 ist die Menge aller Variationen mit Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Variationen mit Wiederholung von n Dingen zur Klasse k (für  ). Sie heißt auch Menge aller Permutationen mit Wiederholung von n Dingen zur Klasse k und hat die oben angegebene Anzahl von Elementen.
). Sie heißt auch Menge aller Permutationen mit Wiederholung von n Dingen zur Klasse k und hat die oben angegebene Anzahl von Elementen.
- Beispiele
- Wenn aus 3 Objekten 11 mal mit Zurücklegen gezogen wird, dann sind 311 = 177.147 verschiedene Auswahlen möglich.
- Bei einer 4-stelligen PIN oder einem Zahlenschloss mit 4 Ringen und je 10 Ziffern gibt es insgesamt 104 = 10000 verschiedene Variationen (0000–9999).
- In der Digitaltechnik verwendete Binärzahlen bestehen nur aus den beiden Ziffern 0 und 1. Mit einer Anordnung von x solchen Ziffern können dementsprechend 2x verschiedene Variationen entstehen. Eine vierstellige Binärzahl beispielsweise kodiert somit 24 = 16 verschiedene Zustände.
Auswahlen ohne Beachtung der Reihenfolge (Kombinationen)
Im Gegensatz zu Variationen (englisch k-permutations) werden bei den Kombinationen (englisch k-combinations) die Reihenfolgen oder Anordnungen der gewählten Elemente außer Acht gelassen, d.h. die Stichproben {a,b,c}, {b,a,c}, {b,c,a} usw. als gleich betrachtet, so dass es für eine gegebene Ausgangsmenge stets weniger Kombinationen als Variationen ihrer Elemente gibt.
Kombination ohne Zurücklegen
Auswahlprobleme ohne Zurücklegen können auf zweierlei Weise untersucht werden. Im klassischen Fall geht man dabei von der Variation ohne Zurücklegen aus, für die es der og. Formel gemäß bei k von n auszuwählenden Elementen
Möglichkeiten gibt. Nun aber können die k ausgewählten Elemente, wie schon bei der Permutation ausgeführt, ihrerseits auf k! verschiedene Weisen angeordnet sein - wenn diese verschiedenen Anordnungen allesamt keine Rolle spielen, also immer wieder als die gleiche Auswahl von Elementen gelten sollen, müssen wir das erhaltene Ergebnis noch einmal durch k! teilen und erhalten damit nur noch
Möglichkeiten. Ein zweiter, insbesondere bei der Auswertung von Bernoulli-Experimenten Anwendung findender Ansatz fasst die Kombination ohne Zurücklegen als ein Anordnungsproblem auf. Die Zahl der möglichen Auswahlen kann dann dadurch ermittelt werden, dass man die Zahl der voneinander unterscheidbaren Anordnungen ausgewählter und nicht ausgewählter Objekte bestimmt, wobei diese selbst nicht mehr voneinander unterscheidbar sein sollen, die gesamte Ausgangsmenge also nur noch in die beiden Objektklassen „ausgewählt“ (z.B. schwarze Kugel mit weißer Nummer) und „nicht ausgewählt“ (z.B. weiße Kugel mit schwarzer Nummer) unterteilt ist.
Wenn man nun untersucht, wie viele verschiedene Anordnungen dieser schwarzen und weißen Kugeln es gibt, wobei nur ihre Farbe eine Rolle spielen soll, ergibt sich gemäß der obigen Formel für die Zahl der Permutationen von Elementen, die jeweils klassenweise nicht unterscheidbar sind:
Ob k dabei die Zahl der ausgewählten Objekte und n−k die Zahl der nicht ausgewählten Objekte ist oder umgekehrt, ist für das Ergebnis unerheblich: Welche der beiden Teilmengen der Ausgangsmenge die interessierende ist, hat keinen Einfluss auf die Anzahl der möglichen Aufteilungen, die auch als Binomialkoeffizient bezeichnet wird.
- Mengendarstellung
- Die Menge
 ist die Menge aller Kombinationen ohne Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Kombinationen ohne Wiederholung von n Dingen zur Klasse k (für  ) und hat die oben angegebene Anzahl von Elementen.
) und hat die oben angegebene Anzahl von Elementen.
- Beispiel
Wenn aus 49 Objekten nun 6 ohne Zurücklegen und ohne Beachtung der Reihenfolge ausgewählt werden sollen, wie dies zum Beispiel bei der Ziehung der Lottozahlen der Fall ist, gibt es dabei
 mögliche Auswahlen.
mögliche Auswahlen.Beim Lotto ist die Reihenfolge egal, ob beispielsweise zuerst die 9 und dann die 17 oder erst die 17 und dann die 9 gezogen wird, spielt für die Gewinnzahlen und die Bestimmung des Lottogewinners keine Rolle. Die Anzahl der möglichen Lösungen errechnet sich aus der Zahl der zunächst 49 und dann 48 Kugeln, die gezogen werden können, also 49 × 48. Da aber die Reihenfolge egal ist, muss berücksichtigt werden, dass das Produkt 2 (= 1 × 2 = 2!) gleichwertige Lösungen umfasst.
Bei drei gezogenen Zahlen ist die Anzahl der Möglichkeiten 49 × 48 × 47, aber weil die Ziehungsreihenfolge der Kugeln egal ist, muss das Produkt durch die Anzahl möglicher Ziehungsreihenfolgen 6 (= 1 × 2 × 3 = 3!) geteilt werden.
Kombination mit Zurücklegen (Repetition)
Sollen aus einer Menge von n Elementen k Elemente ausgewählt werden, wobei ihre Reihenfolge weiterhin ohne Belang sein soll, sie sich aber nun auch wiederholen dürfen, wie das z.B. beim Ziehen mit Zurücklegen möglich ist, ergibt sich für die Zahl der Möglichkeiten folgende Formel:
- Mengendarstellung
- Die Menge
 ist die Menge aller Kombinationen mit Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Kombinationen mit Wiederholung von n Dingen zur Klasse k (für  ) und hat die oben angegebene Anzahl von Elementen. Hierbei bezeichnet xi die Anzahl des Auftretens des i-ten Elements der Stichprobe.
) und hat die oben angegebene Anzahl von Elementen. Hierbei bezeichnet xi die Anzahl des Auftretens des i-ten Elements der Stichprobe.
- Beispiele
- Eine Anwendung davon ist das sogenannte „Gummibärchenorakel“, bei dem man k = 5 Bärchen aus einer Tüte mit Gummibärchen in 5 verschiedenen Farben (n=5)) auswählt. Demnach gibt es
 verschiedene Kombinationen.
verschiedene Kombinationen. - Aus einer Urne mit 5 nummerierten Kugeln (n = 5) werden drei Kugeln gezogen (k = 3) und anschließend zurückgelegt. Man kann also bei der ersten Ziehung aus 5 Kugeln auswählen, und bei der zweiten und dritten ebenfalls. Wenn man die Reihenfolge der Ziehungen nicht berücksichtigt, gibt es davon

verschiedene Kombinationen. Diese 35 Kombinationen von 5 Dingen zur Klasse 3 mit Wiederholung, also 3-elementige Multimengen mit Elementen aus der Ausgangsmenge {1,2,3,4,5}, entsprechen dabei, wie die nebenstehende Grafik zeigt, interessanterweise genau den 35 Kombinationen von 7 Dingen zur Klasse 3 ohne Wiederholung, also der Zahl 3-elementiger Teilmengen einer insgesamt 7-elementigen Ausgangsmenge:
Zusammenfassung
ohne Wiederholung
(von n Elementen)

mit Wiederholung
(von r + s + ... + t = n Elementen,
von denen jeweils r, s ... t nicht unterscheidbar sind)

Permutation



n bezeichnet die Anzahl der vorhandenen Elemente, und k die Anzahl der Elemente, die ausgewählt werden:ohne Wiederholung


mit Wiederholung


Variation



Kombination



Siehe auch
Literatur
- Jacobus van Lint, Richard M. Wilson: A Course in Combinatorics. Cambridge University Press 1992, ISBN 0-521-42260-4
- Karl Bosch: Elementare Einführung in die Wahrscheinlichkeitsrechnung. vieweg+Teubner Verlag 2003, ISBN 3-528-77225-5
Weblinks
 Wiktionary: Kombinatorik – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wiktionary: Kombinatorik – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen- Kombinatorik (combinatorial analysis) in Springers Encyclopaedia of Mathematics (englisch)
- Modul Kombinatorik beim MathePrisma
- Links zum Thema Kombinatorik im Open Directory Project
- Surveys in Combinatorics
- Kombinatorik (Vorlesungsskript, PDF; 554 kB)
Wikimedia Foundation.










