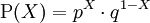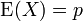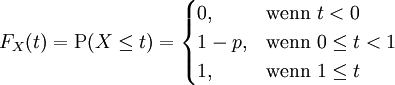- Bernoulliversuch
-
Zufallsgrößen mit einer Null-Eins-Verteilung bzw. Bernoulli-Verteilung benutzt man zur Beschreibung von zufälligen Ereignissen, bei denen nur zwei mögliche Versuchsausgänge interessieren, das zufällige Ereignis (Erfolg) und sein komplementäres Ereignis (Misserfolg). Beispiele hierfür sind:
- Werfen einer Münze (Wappen p = 1 / 2, Zahl q = 1 / 2)
- Werfen eines Würfels, wobei nur eine „6“ als Erfolg gewertet wird: p = 1 / 6, q = 5 / 6.
- Qualitätsprüfung (einwandfrei, nicht einwandfrei)
- Anlagenprüfung (funktioniert, funktioniert nicht)
Die Bezeichnung Bernoulli-Versuch (Bernoullian trials nach Jakob I. Bernoulli) wurde erstmals 1937 in dem Buch Introduction to Mathematical Probability von James Victor Uspensky[1] verwendet.
Inhaltsverzeichnis
Definition
Eine diskrete Zufallsgröße X unterliegt der Null-Eins-Verteilung bzw. Bernoulli-Verteilung mit dem Parameter p, wenn sie die folgenden Einzelwahrscheinlichkeiten besitzt.
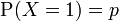 und
und 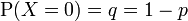 .
.
Letzteres kann man auch durch den geschlossenen Ausdruck
ersetzen, denn es ist
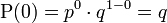 und
und 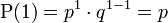
Eine Wiederholung von vielen identischen Versuchen, bei denen jeder Einzelversuch der Bernoulli-Verteilung genügt, wird Bernoullisches Versuchsschema oder Bernoulli-Prozess genannt.
Eigenschaften
Erwartungswert
Die Bernoulli-Verteilung mit Parameter p hat den Erwartungswert:
Varianz
Die Bernoulli-Verteilung besitzt die Varianz:
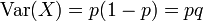 , denn:
, denn: 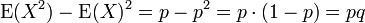 .
.
Verteilungsfunktion
Die Bernoulli-Verteilung besitzt die Verteilungsfunktion:
Beziehung zu anderen Verteilungen
Beziehung zur Binomialverteilung
Die Bernoulli-Verteilung ist ein Spezialfall der Binomialverteilung für n = 1. Mit anderen Worten, die Summe von Bernoulli-verteilten Zufallsgrößen mit identischem Parameter p genügt der Binomialverteilung. Die Binomialverteilung ist die n-fache Faltung der Bernoulli-Verteilung bei gleichem Parameter p bzw. mit gleicher Wahrscheinlichkeit p.
Beziehung zur Poisson-Verteilung
Die Summe von Bernoulli-verteilten Zufallsgröße genügt für
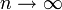 ,
, 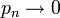 und
und 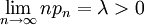 einer Poisson-Verteilung mit dem Parameter λ.
einer Poisson-Verteilung mit dem Parameter λ.Einzelnachweise
- ↑ James Victor Uspensky: Introduction to Mathematical Probability, McGraw-Hill, New York 1937
Siehe auch
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.