- Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I
-
Der gödelsche Unvollständigkeitssatz ist einer der wichtigsten Sätze der modernen Logik. Er beschäftigt sich mit der Ableitbarkeit von Aussagen in formalen Theorien. Der Satz zeigt die Grenzen der formalen Systeme ab einer bestimmten Mächtigkeit auf und weist nach, dass man in Systemen wie der Arithmetik nicht alle Aussagen formal beweisen oder widerlegen kann.
Der Satz findet sich in der Arbeit von Kurt Gödel: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. in: Monatshefte für Mathematik und Physik 38 (1931), S. 173 ff.
Inhaltsverzeichnis
Grundbegriffe
Aussagen sind dabei Folgen von Zeichen, die ähnlich wie ein Programm einer Programmiersprache einer gewissen Syntax genügen müssen und die mittels einer Semantik eine Bedeutung erhalten und sich dadurch in wahre und falsche Aussagen unterteilen lassen (wobei zu einer gegebenen Aussage nicht unbedingt sofort klar ist, ob sie wahr oder falsch ist), siehe Formales System. Für gewöhnlich lassen sich dabei zu einer Aussage auch leicht komplementäre Aussagen derart konstruieren, dass entweder die Aussage selbst oder die komplementäre Aussage wahr ist, aber niemals beide zugleich.
Die Aufgabe einer formalen Theorie ist es dann, aus bestimmten Grundaussagen (Axiome), die generell als wahr angenommen werden, über allgemein akzeptierte Ableitungsregeln weitere wahre Aussagen abzuleiten. Eine Folge solcher Ableitungen nennt man dann Beweis der entsprechenden abgeleiteten Aussage, da sie die Allgemeingültigkeit der Aussage zeigt (siehe gödelscher Vollständigkeitssatz). Im Idealfall wünscht man sich, dass aus der Menge der Grundaussagen und den Ableitungsregeln alle wahren Aussagen abgeleitet, also bewiesen werden können. Ein derartiges System nennt man dann vollständig (andernfalls unvollständig). Eine formale Theorie sollte zudem auch widerspruchsfrei sein, das heißt, es lassen sich keine falschen Aussagen ableiten. Genauer formuliert, lassen sich nicht gleichzeitig eine Aussage und eine dazu (im obigen Sinne) komplementäre Aussage ableiten. Eine formale Theorie, die dem nicht genügt, nennt man widersprüchlich.
Gödels Satz
Satz
Der Mathematiker Kurt Gödel wies mit seinem im Jahre 1931 veröffentlichten Unvollständigkeitssatz nach, dass man in Systemen wie der Arithmetik nicht alle Aussagen formal beweisen oder widerlegen kann. Sein Satz besagt:
- Jedes hinreichend mächtige formale System ist entweder widersprüchlich oder unvollständig.
Eine einfache Formulierung des ersten Unvollständigkeitssatzes sowie des daraus unmittelbar folgenden zweiten gödelschen Unvollständigkeitssatzes lautet: In jedem formalen System der Zahlen, das zumindest eine Theorie der natürlichen Zahlen (
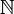 ) enthält, gibt es einen unentscheidbaren Satz, also einen Satz, der nicht beweisbar und dessen Widerlegung ebenso wenig beweisbar ist (1. gödelscher Unvollständigkeitssatz). Daraus folgt unmittelbar, dass kein formales System der Zahlen, das zumindest eine Theorie der natürlichen Zahlen (
) enthält, gibt es einen unentscheidbaren Satz, also einen Satz, der nicht beweisbar und dessen Widerlegung ebenso wenig beweisbar ist (1. gödelscher Unvollständigkeitssatz). Daraus folgt unmittelbar, dass kein formales System der Zahlen, das zumindest eine Theorie der natürlichen Zahlen (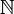 ) enthält, sich innerhalb seiner selbst als widerspruchsfrei beweisen lässt (2. gödelscher Unvollständigkeitssatz).
) enthält, sich innerhalb seiner selbst als widerspruchsfrei beweisen lässt (2. gödelscher Unvollständigkeitssatz).Beweis
Gödels Argumentation läuft auf eine Abzählung aller Sätze innerhalb des formalen Systems hinaus, jeder Satz erhält eine eigene Nummer. Er konstruiert dann mit Hilfe einer Diagonalisierung eine Aussage der Form: „Der Satz mit der Nummer x ist nicht ableitbar“ und zeigt, dass es eine Einsetzung für x gibt, so dass x die Nummer dieser Aussage ist. Insgesamt erhält er einen Satz der Form „Ich bin nicht ableitbar“. Es gibt nun zwei Möglichkeiten: Entweder dieser „Satz x“ ist wahr, dann ist er nicht ableitbar (genau das ist sein Inhalt: Ich bin nicht ableitbar!). Oder „Satz x“ ist falsch, dann muss der Satz ableitbar sein. Ein formales System, aus dem ein falscher Satz abgeleitet werden kann, ist aber widersprüchlich. Demnach kann dieser Satz nur wahr sein, wenn das formale System unvollständig ist, oder falsch, wenn das formale System widersprüchlich ist (siehe hierfür auch das klassische Problem des Lügner-Paradox).
Man beachte: Falls das formale System nicht widersprüchlich ist, ist der Satz mit Nummer x und der Bedeutung „Satz x ist nicht ableitbar“ damit gezeigt. Wir vertrauen auf diesen „Beweis“, obwohl es innerhalb des Systems keine Ableitung gibt, die zu diesem Satz führt.
Damit obiger Ansatz funktioniert, muss das zugrundegelegte formale System also mindestens Zählungen und eine Multiplikation mit einer Konstanten größer als 1 (für Kodierungszwecke) erlauben. Für zu einfache Systeme gilt der Unvollständigkeitssatz daher nicht. Die Möglichkeit von Addition und Multiplikation sind ganz wesentliche Eigenschaften in vielen Theorien, so dass hier dieser Satz gilt. Insbesondere muss aber eine Substitution wie im Beweis Gödels möglich sein. Es gibt sehr einfache Systeme, für die diese Bedingungen erfüllt sind.
Nun könnte man sich dadurch behelfen, dass man für alle Sätze, die weder bewiesen noch widerlegt werden können, einfach festlegt, ob sie als wahr oder falsch gelten. Das formale System würde dann durch diese zusätzlichen Axiome erweitert. Lesen wir jedoch erneut den Unvollständigkeitssatz, so sehen wir, dass auch hier die Voraussetzungen erfüllt sind und somit auch das erweiterte System unvollständig bleibt, da stets unbeweisbare Sätze übrigbleiben.
Bedeutung des Unvollständigkeitssatzes
Gödel versetzte mit seinem Unvollständigkeitssatz einem Ansatz von David Hilbert zur vollständigen Begründung und Formalisierung der Mathematik einen schweren Schlag. Dieser Ansatz ist als Hilbertprogramm bekannt geworden und wurde von ihm im Jahre 1921 veröffentlicht. Hilbert hatte vorgeschlagen, die Widerspruchsfreiheit von komplexeren Systemen durch diejenige einfacherer Systeme nachzuweisen. Hintergrund ist der, dass einem Beweis zur Widerspruchsfreiheit eines Systems, der in diesem System selbst gegeben ist, nicht getraut werden kann. Der Grund ist, dass sich aus einem Widerspruch heraus alles beweisen lässt (Ex falso quodlibet), also ließe sich aus einem Widerspruch im System auch die Widerspruchsfreiheit des Systems beweisen. Daher sollte die Widerspruchsfreiheit in einem einfacheren System bewiesen werden.
Eine streng formalisierte Prädikatenlogik erster Stufe war eines von Hilberts Konzepten. Am Ende seines Programms sollte die gesamte Mathematik auf die einfache Arithmetik zurückgeführt und auf ein axiomatisches System gestellt werden, aus dem alle mathematischen Sätze streng ableitbar sind.
Gödels Arbeit war durch Hilberts Programm motiviert. Er verwendete die von Hilbert vorgeschlagenen Methoden, um seinen Unvollständigkeitssatz zu zeigen. Gödel bewies auch den folgenden Satz
- Ein System kann nicht zum Beweis seiner eigenen Widerspruchsfreiheit verwendet werden.
Gödel hatte damit gewissermaßen Hilbert mit dessen Methoden gezeigt, dass der Vorschlag nicht funktioniert.
Die Folge daraus ist, dass man die Korrektheit von (gewissen) formalen Systemen als gegeben annehmen muss, sie lassen sich nicht beweisen.
Ein anderer Ansatz, der unüberbrückbare Lücken in Hilberts Programm nachweist, stammt von dem Mathematiker Alan Turing. Er erfand die Turingmaschine und formulierte deren Halteproblem.
Philosophische Interpretationen
Obwohl Gödel sich im Laufe seines Lebens wiederholt als Platoniker zu erkennen gab, wurde sein Unvollständigkeitssatz wiederholt in einem subjektivistischen Sinn interpretiert. Auch schien Gödels Teilnahme am Wiener Kreis eine Nähe des Unvollständigkeitssatzes mit dem logischen Positivismus nahezulegen, der dem Platonismus in vielerlei Hinsicht entgegengesetzt ist. Gödels zurückhaltende, konfliktscheue Art trug dazu bei, die Fehlinterpretationen am Leben zu erhalten.
Gödel selbst verstand seinen Satz jedoch insbesondere als einen Schlag gegen den von Hilbert propagierten Formalismus in der Mathematik, der in letzter Konsequenz die gesamte Mathematik zu einem rein formalen Gebilde ohne Bezug zur „realen Welt“ machen sollte. Für Gödel als Platoniker waren jedoch die mathematischen Objekte durchaus „real“. Sie waren zwar nicht durch Sinneswahrnehmungen zu bestätigen (wie es die Positivisten einforderten), doch waren sie der Erkenntnis zugänglich. Der Unvollständigkeitssatz zeigte für Gödel, dass man dieser Realität nicht mit rein formalen Mitteln beikommen konnte.
Obwohl Gödel sich in seiner Grundhaltung gegenüber dem damals bedeutsamen logischen Positivismus nicht sehr von Ludwig Wittgenstein unterschied, der eine Realität jenseits der möglichen Bedeutung von Sätzen anerkannte (und sie sogar für wichtiger hielt als das Sagbare), hielten Wittgenstein und Gödel Zeit ihres Lebens nicht viel voneinander. In Wittgensteins Werk wird der Unvollständigkeitssatz eher abschätzig behandelt. Für Wittgenstein taugte der Satz lediglich für „logische Kunststücke“. Gödel hingegen wies in späteren Interviews jeglichen Einfluss Wittgensteins auf sein eigenes Denken weit von sich.
Genauere Formulierung
Der gödelsche Satz besagt genauer, dass jedes Beweissystem für die Menge der wahren arithmetischen Formeln unvollständig ist (sofern man voraussetzt, dass die Arithmetik widerspruchsfrei ist – was, wie Gödel auch zeigt, nicht mit Mitteln der untersuchten Theorie allein bewiesen werden kann). Das heißt:
In jeder formalen Theorie, welche mindestens so mächtig wie die Theorie der natürlichen Zahlen (Peano-Arithmetik) ist, bleiben wahre (und falsche) arithmetische Formeln übrig, die nicht innerhalb der Theorie beweisbar (widerlegbar) sind. Paul Cohen bewies 1963, dass sowohl das Auswahlaxiom als auch die Kontinuumshypothese auf Grundlage der Zermelo-Fraenkel-Mengenlehre formal unentscheidbar sind. Er fand damit die ersten Beispiele mathematisch bedeutsamer unentscheidbarer Sätze, deren Existenz Gödel bewiesen hatte.
Damit eine Theorie (in der Prädikatenlogik erster Stufe, PL1) die Voraussetzungen für die Unvollständigkeit erfüllt, muss gelten:
- Zu jeder durch einen Ausdruck G(x) beschriebenen Menge ist das Komplement beschreibbar.
- Zu jeder durch einen Ausdruck G(x) beschriebenen Menge M ist die Menge M*={x|d(x)∈M} beschreibbar; Dabei ist d(x) die Diagonalisierung von x.
- Die Menge der beweisbaren Ausdrücke der Theorie ist durch einen Ausdruck der Form G(x) beschreibbar.
Nach dem Satz von Löwenheim-Skolem findet man zu jeder Theorie in PL1 ein Modell mit der Mächtigkeit der Signatur. Für normale Theorien existiert also ein abzählbares Modell, beispielsweise die natürlichen Zahlen (das heißt es lässt sich für jede Theorie in PL1 auch ein Modell finden, in dem die Objekte natürliche Zahlen sind). Die Idee von Gödel war, Formeln der Theorie selbst zum Objekt derselben zu machen. Dazu wurden die Formeln gödelisiert, das heißt eine (injektive) Abbildung von Formeln auf natürliche Zahlen gebildet. Das kann man zum Beispiel dadurch erreichen, dass man jedem Symbol der Signatur eine Zahl zuordnet und einer Symbolkette entsprechend eine Kette von Zahlen. Ordnet man der 0 die 1 und = die 2 zu, so ist die Gödelnummer der Formel (in dem Spezialfall) 0=0 die 121. Die Zahlenkette wird dann durch Exponentieren in eine einzelne Zahl übersetzt. Es lassen sich auch die syntaktisch wohlgeformten, und schließlich die beweisbaren Formeln durch arithmetische Ausdrücke (Addition, Multiplikation, Exponentiation) beschreiben.
Die Diagonalisierung in Gödels Beweis ist nun eine Anwendung eines Ausdrucks P(x) auf die eigene Gödelnummer. Ist die Gödelnummer des Ausdrucks (und damit der Zeichenreihe) P(x) zum Beispiel 12345, so ist die Diagonalisierung d der Zahl 12345 die Gödelnummer von P(12345) (selbstverständlich hat eine Zahl, hier 12345, auch eine Gödelnummer, die entsteht, indem man alle vorkommenden Ziffern gödelisiert).
Besagt der Ausdruck Bew(x) also, dass x ableitbar ist, so sagt B(x)=¬Bew(d(x)), dass die Formel mit der Gödelnummer d(x) nicht ableitbar ist. Ist nun zum Beispiel 12345 die Gödelnummer von B(x), so ist B(12345) eine nicht ableitbare Aussage. Diese Aussage besagt dann nämlich: Die Formel mit der Gödelnummer d(12345) ist nicht ableitbar. 12345 ist aber die Gödelnummer von B(x), also d(12345) die Gödelnummer von B(12345). Also sagt B(12345): Ich bin nicht ableitbar. Wenn PA korrekt ist, so ist dieser Satz wahr (in PA), aber nicht ableitbar.
Gödels ursprünglicher Beweis ging noch weiter. Er wollte Rückgriffe auf die Semantik, insbesondere die Korrektheit, vermeiden. Deswegen bewies er seinen Unvollständigkeitssatz unter der Voraussetzung der ω-Konsistenz: Eine Theorie ist ω-inkonsistent, wenn ein Ausdruck mit einer einzigen freien Variable x existiert, für den
 ableitbar ist, zugleich aber für alle n < ω
ableitbar ist, zugleich aber für alle n < ω  ableitbar ist.
ableitbar ist.Rosser erweiterte das gödelsche Resultat, indem er einen Unvollständigkeitsbeweis lieferte, für den nicht die Menge der Ausdrücke, deren Diagonalisierung beweisbar ist, beschrieben wird, sondern eine zu dieser Menge disjunkte Obermenge der Ausdrücke, deren Diagonalisierung widerlegbar ist. Dadurch ist auch der Bezug auf die ω-Konsistenz überflüssig.
Gödels zweiter Unvollständigkeitssatz ist eine leicht zu sehende Konsequenz aus dem ersten. Da Gödel beweisbare Aussagen innerhalb der Prädikatenlogik formalisierte (beispielsweise durch das Prädikat Bew(x)), lässt sich auch folgende Aussage bilden:
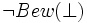 , wobei
, wobei 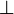 die Gödelnummer von einer beliebigen Kontradiktion, zum Beispiel
die Gödelnummer von einer beliebigen Kontradiktion, zum Beispiel 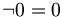 , ist. Die Aussage
, ist. Die Aussage 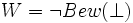 behauptet die Nichtbeweisbarkeit einer Kontradiktion, und damit die Widerspruchsfreiheit der gesamten Theorie (der Peano-Arithmetik). W ist in PA nicht beweisbar. Um die Nicht-Beweisbarkeit zu zeigen, wird eine Fixpunktkonstruktion verwendet. Sei g(x) die Gödelisierungsfunktion, A eine Aussage, B(x) ein Prädikat. A heißt Fixpunkt für B(x), wenn
behauptet die Nichtbeweisbarkeit einer Kontradiktion, und damit die Widerspruchsfreiheit der gesamten Theorie (der Peano-Arithmetik). W ist in PA nicht beweisbar. Um die Nicht-Beweisbarkeit zu zeigen, wird eine Fixpunktkonstruktion verwendet. Sei g(x) die Gödelisierungsfunktion, A eine Aussage, B(x) ein Prädikat. A heißt Fixpunkt für B(x), wenn 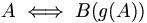 beweisbar ist. Über einfache aussagenlogische Konstruktionen lässt sich beweisen, dass
beweisbar ist. Über einfache aussagenlogische Konstruktionen lässt sich beweisen, dass 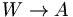 beweisbar ist, wenn A Fixpunkt von
beweisbar ist, wenn A Fixpunkt von 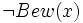 ist. Außerdem kann leicht gezeigt werden, dass, wenn A Fixpunkt von
ist. Außerdem kann leicht gezeigt werden, dass, wenn A Fixpunkt von 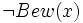 ist, A nicht beweisbar ist, falls PA konsistent ist. Daraus folgt dann, dass W nicht beweisbar ist.
ist, A nicht beweisbar ist, falls PA konsistent ist. Daraus folgt dann, dass W nicht beweisbar ist.Durch diese erstaunlichen Sätze ist der Mathematik eine prinzipielle Grenze gesetzt: Nicht jeder wahre mathematische Satz kann aus den wie auch immer gewählten Axiomen eines mathematischen Teilgebietes (zum Beispiel Arithmetik, Geometrie, Algebra etcetera) formal abgeleitet werden.
Viel Verwirrung entsteht aus dem Zusammenhang der gödelschen Unvollständigkeitssätze mit dem gödelschen Vollständigkeitssatz. Hier ist zu beachten, dass der Begriff der Vollständigkeit in zwei verschiedenen Bedeutungen gebraucht wird. Der Vollständigkeitssatz beweist die semantische Vollständigkeit der Prädikatenlogik der ersten Stufe, behandelt also eine Eigenschaft von formalen Systemen. Der Unvollständigkeitssatz hingegen beweist, dass gewisse Mengen von Ausdrücken nicht vollständig im klassischen Sinne sind.
Ein häufiger Fehlschluss aus dem Unvollständigkeitssatz ist, dass gewisse mathematische Objekte, wie z.B. die natürlichen Zahlen nicht mit einer vollständigen Menge von Ausdrücken formalisierbar sind. Man erkennt aber sofort, dass die Menge aller Ausdrücke (in einer geeigneten formalen Sprache), die in der Menge der natürlichen Zahlen gelten, sowohl vollständig ist als auch die natürlichen Zahlen formalisiert. Eine Konsequenz aus dem Unvollständigkeitssatz ist aber, dass eine solche Menge nicht entscheidbar sein kann, womit sie eine in vielen Bereichen der Logik notwendige Eigenschaft nicht erfüllt.
Ein weiterer Fehlschluss ist, dass die meisten in der Mathematik benutzten Theorien unvollständig sind. Es gibt aber einige wichtige vollständige Theorien, wie z.B. die Theorie der algebraisch abgeschlossenen Körper von Charakteristik p, die Theorie der dichten linearen Ordnungen ohne grösstes und kleinstes Element oder Tarskis Axiomatisierung der euklidischen Geometrie.
Sonstiges
Gödel nannte seinen Aufsatz Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I, weil er plante, einen zweiten Aufsatz zu verfassen, in dem er den Beweis genauer erläutern wollte. Der erste Aufsatz fand jedoch bereits so große Anerkennung, dass der Bedarf für einen zweiten entfiel, der daher auch nie geschrieben wurde.
Konkret bezog sich Gödels Aufsatz auf die Principia Mathematica, ein großes formales System, das Bertrand Russell und Alfred North Whitehead zwischen 1910 und 1913 veröffentlichten. Gödel zeigte jedoch auf, dass jedes System mit der gleichen Mächtigkeit wie die Principia Mathematica ebenso anfällig ist.
Weiterhin konnte Gerhard Gentzen zeigen, dass eine konstruktive Mathematik und Logik durchaus widerspruchsfrei ist. Hier zeigt sich ein Grundlagenstreit der Mathematik. Der Philosoph Paul Lorenzen hat eine widerspruchsfreie Logik und Mathematik erarbeitet (Methodischer Konstruktivismus), und sein Buch Metamathematik (1962) eigens geschrieben, um zu zeigen, dass der gödelsche Unvollständigkeitssatz keinen Einwand gegen einen widerspruchsfreien Aufbau der Mathematik darstellt.
Eine interessante und relativ leicht verständliche Erklärung von Gödels Satz und seinen Implikationen gibt das Buch Gödel, Escher, Bach von Douglas Hofstadter.
Siehe auch
- Referenzproblem
- Goodstein-Folgen haben eine innerhalb der Peano-Arithmetik formulierbare, aber nicht beweisbare Eigenschaft.
Literatur
- Kurt Gödel: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik 38, 1931, S.173–198.
- Kurt Gödel: Diskussion zur Grundlegung der Mathematik: Erkenntnis 2. Monatshefte für Math. und Physik, 1931–32, S.147–148.
- Ernest Nagel u. James R. Newman: Der Gödelsche Beweis. 8. Auflage 2007. ISBN 978-3-486-45218-1
- Douglas R. Hofstadter: Gödel, Escher, Bach, ein Endloses Geflochtenes Band. München 1991 ISBN 3-423-30017-5
- Paul Lorenzen: Metamathematik. Mannheim 1962. ISBN 3-86025-870-2
- Max Woitschach: Gödel, Götzen und Computer: eine Kritik der unreinen Vernunft. Stuttgart 1986. ISBN 3-87959-294-2
- Paul Lorenzen: Lehrbuch der konstruktiven Wissenschaftstheorie. Stuttgart 2000. ISBN 3-476-01784-2
- Wolfgang Stegmüller: Unvollständigkeit und Unentscheidbarkeit: die mathematischen Resultate von Gödel, Church, Kleene, Rosser und ihre erkenntnistheoretische Bedeutung. Wien 1973. (ISBN 3-211-81208-3)
- Sybille Krämer: Symbolische Maschinen: die Idee der Formalisierung in geschichtlichem Abriß. Darmstadt 1988. ISBN 3-534-03207-1
- Ludwig Fischer: Die Grundlagen der Philosophie und der Mathematik. Leipzig 1933.
- Raymond Smullyan: Dame oder Tiger – Logische Denkspiele und eine mathematische Novelle über Gödels große Entdeckung. Fischer-Verlag Frankfurt am Main 1983. Das amerikanische Original erschien bei Afred A. Knopf, New York 1982.
- Raymond Smullyan: To Mock a Mockingbird. 1985
- Raymond Smullyan: Forever undecided: a puzzle guide to Gödel. 1987
- Raymond Smullyan: Gödel´s Incompleteness Theorems. Oxford Logic Guides. Oxford University Press, 1992
- Max Urchs, Klassische Logik: eine Einführung, Berlin (1993). - ISBN 3-05-002228-0. (dort im Kapitel: Theorien erster Ordnung, S. 137 - 149)
- Norbert Domeisen: Logik der Antinomien. Bern 1990. ISBN 3-261-04214-1, Zentralblatt MATH
Weblinks
- Die Grenzen der Berechenbarkeit
- Einstieg in die Zusammenhänge des Unvollständigkeitssatzes
- Christopher v. Bülow: Der erste Gödelsche Unvollständigkeitssatz. Eine Darstellung für Logiker in spe. März 1992 (PDF, 355 kB)
- Eine englische Übersetzung von Gödels Aufsatz Über formal unentscheidbare Aussagen. (PDF, 328 KB)
Wikimedia Foundation.
