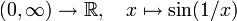- Zusammenhang (Topologie)
-
In der mathematischen Topologie gibt es verschiedene Begriffe, die die Art und Weise des Zusammenhangs eines topologischen Raumes beschreiben. Im Allgemeinen heißt ein topologischer Raum X zusammenhängend, falls es nicht möglich ist, ihn in zwei disjunkte, nichtleere, offene Teilmengen aufzuteilen. Ein Teilraum eines topologischen Raumes heißt zusammenhängend, wenn er unter der induzierten Topologie zusammenhängend ist.
Eine maximale zusammenhängende Teilmenge eines topologischen Raumes heißt Zusammenhangskomponente.
Inhaltsverzeichnis
Formale Definition
Für einen topologischen Raum
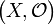 sind folgende Aussagen äquivalent:
sind folgende Aussagen äquivalent:- X ist zusammenhängend.
- X kann nicht in zwei disjunkte nichtleere offene Mengen zerlegt werden:
- X kann nicht in zwei disjunkte nichtleere abgeschlossene Mengen zerlegt werden:
- X und
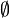 sind die beiden einzigen Mengen, die zugleich offen und abgeschlossen sind.
sind die beiden einzigen Mengen, die zugleich offen und abgeschlossen sind. - Die einzigen Mengen mit leerem Rand sind X und
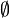 .
. - X kann nicht als Vereinigung zweier nichtleerer getrennter Mengen geschrieben werden.
- Jede stetige Abbildung von X in einen diskreten topologischen Raum ist konstant.
- Jede lokal konstante Funktion ist konstant.
Globale Zusammenhangsbegriffe
Die folgenden Begriffe beziehen sich immer auf den ganzen Raum, sind also globale Eigenschaften:
Total unzusammenhängend
Ein Raum ist total unzusammenhängend, falls er keine zusammenhängende Teilmenge mit mehr als einem Punkt besitzt, wenn also alle Zusammenhangskomponenten einpunktig sind. Jeder diskrete topologische Raum ist total unzusammenhängend. In diesem Fall sind die (einpunktigen) Zusammenhangskomponenten offen. Ein Beispiel für einen nicht diskreten total unzusammenhängenden Raum ist die Menge der rationalen Zahlen
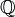 mit der von
mit der von 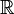 induzierten Topologie.
induzierten Topologie.Wegzusammenhängend
Ein topologischer Raum X ist wegzusammenhängend (oder pfad-zusammenhängend oder kurvenweise zusammenhängend), falls es für jedes Paar von Punkten x, y aus X einen Weg p von x nach y gibt, d.h. eine stetige Abbildung
![p : [0,1] \to X](/pictures/dewiki/99/c2908a2ef3893f387f5f8042ee82d2b9.png) mit p(0) = x und p(1) = y.
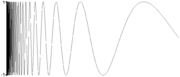
mit p(0) = x und p(1) = y.Wegzusammenhängende Räume sind immer zusammenhängend. Etwas überraschend ist auf den ersten Blick jedoch vielleicht, dass es Räume gibt, die zusammenhängend, aber nicht wegzusammenhängend sind. Ein Beispiel ist die Vereinigung des Graphen von
mit einem Abschnitt der y-Achse zwischen ‒1 und 1. Da in jeder Umgebung der Null auch ein Stück des Graphen liegt, kann man die y-Achse nicht vom Graphen als eine offene Teilmenge abtrennen; die Menge ist also zusammenhängend. Andererseits gibt es keinen Weg von einem Punkt auf dem Graphen zu einem Punkt auf der y-Achse, also ist diese Vereinigung nicht wegzusammenhängend.
Einfach zusammenhängend
Ein Raum ist einfach zusammenhängend, falls er wegzusammenhängend ist und sich jeder geschlossene Weg auf einen Punkt zusammenziehen lässt, d.h. nullhomotop ist. Die zweite Bedingung ist dazu äquivalent, dass die Fundamentalgruppe trivial ist. Das Komplement des farbig eingezeichneten Gebietes ist z. B. in beiden Fällen der obersten Zeichnung nicht „einfach zusammenhängend“; im Falle der unteren Hälfte könnte es sich bei dem weiß eingezeichneten Gebiet etwa um eine Darstellung der Topologie der Oberfläche einer „Kugel mit vier Henkeln“ handeln, wobei die durch die Henkel erzeugten „Löcher“ dem violett gefärbtem Gebiet entsprechen.
n-zusammenhängend
Ist n eine nichtnegative ganze Zahl, so heißt ein topologischer Raum X n-zusammenhängend, falls alle Homotopiegruppen
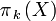 für
für 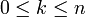 trivial sind. "0-zusammenhängend" ist also ein Synonym für "wegzusammenhängend", und "1-zusammenhängend" bedeutet dasselbe wie "einfach zusammenhängend" im oben definierten Sinne.
trivial sind. "0-zusammenhängend" ist also ein Synonym für "wegzusammenhängend", und "1-zusammenhängend" bedeutet dasselbe wie "einfach zusammenhängend" im oben definierten Sinne.Zusammenziehbar
Ein Raum X ist zusammenziehbar, falls er homotopieäquivalent zu einem Punkt ist, d.h. die Identität auf X homotop zu einer konstanten Abbildung ist. Zusammenziehbare Räume haben daher aus topologischer Sicht ähnliche Eigenschaften wie ein Punkt, insbesondere sind sie immer einfach zusammenhängend. Aber die Umkehrung gilt nicht: n-Sphären mit festem Radius sind nicht zusammenziehbar, obwohl sie für
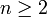 einfach zusammenhängend sind.
einfach zusammenhängend sind.Lokale Zusammenhangsbegriffe
Die folgenden Begriffe sind lokale Eigenschaften, sie machen also Aussagen über das Verhalten in Umgebungen von Punkten:
Lokal zusammenhängend
Ein Raum ist lokal zusammenhängend, falls es zu jeder Umgebung eines Punktes eine zusammenhängende kleinere Umgebung dieses Punktes gibt. Jeder Punkt besitzt dann eine Umgebungsbasis aus zusammenhängenden Mengen.
Ein lokal zusammenhängender Raum kann durchaus aus mehreren Zusammenhangskomponenten bestehen. Aber auch ein zusammenhängender Raum muss nicht unbedingt lokal zusammenhängend sein: Der „Kamm“ bestehend aus der Vereinigung der Intervalle
![[0,1]\times \{1/n\}](/pictures/dewiki/53/508184f49a9f942ebf77e9589452402a.png) ,
, ![[0,1]\times \{0\}](/pictures/dewiki/54/64eff75cea2f1c4f6bfa27484e678529.png) und dem Intervall
und dem Intervall ![\{0\} \times [0,1]](/pictures/dewiki/52/448af289a5d351c8d943b19c90c0e56c.png) ist zusammenhängend, doch jede genügend kleine Umgebung des Punktes (1,0) enthält unendlich viele nicht zusammenhängende Intervalle.
ist zusammenhängend, doch jede genügend kleine Umgebung des Punktes (1,0) enthält unendlich viele nicht zusammenhängende Intervalle.Lokal wegzusammenhängend
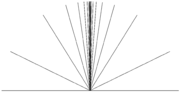
Ein Raum ist lokal wegzusammenhängend, falls jeder Punkt eine lokale Basis bestehend aus wegzusammenhängenden Mengen besitzt. Ein lokal wegzusammenhängender Raum ist wegzusammenhängend genau dann, wenn er zusammenhängend ist. Das oben gegebene Beispiel mit dem Graphen von sin(1/x) und der y-Achse ist daher nicht lokal wegzusammenhängend. Weiterhin ist das 'Buch' wegzusammenhängend, aber nicht lokal wegzusammenhängend für alle Punkte außer dem Schnittpunkt aller Geradenstücke.
Lokal einfach zusammenhängend
Ein Raum ist lokal einfach zusammenhängend, wenn jede Umgebung eines Punktes eine evtl. kleinere, einfach zusammenhängende Umgebung enthält.
Mannigfaltigkeiten sind lokal einfach zusammenhängend.
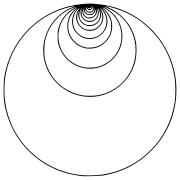
Ein Beispiel für einen nicht lokal einfach zusammenhängenden Raum sind die „Hawaiischen Ohrringe“: Die Vereinigung von Kreisen mit Radien 1 / n als Teilmenge des
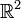 , so dass sich alle Kreise in einem Punkt berühren. Dann enthält jede Umgebung um den Berührpunkt einen geschlossenen Kreis, und ist daher nicht einfach zusammenhängend.
, so dass sich alle Kreise in einem Punkt berühren. Dann enthält jede Umgebung um den Berührpunkt einen geschlossenen Kreis, und ist daher nicht einfach zusammenhängend.Semilokal einfach zusammenhängend
Ein Raum X ist semilokal einfach zusammenhängend, falls jeder Punkt eine Umgebung U besitzt, so dass sich jede Schleife in U in X zusammenziehen lässt (in U muss sie nicht notwendigerweise zusammenziehbar sein, daher nur semilokal).
Semilokal einfach zusammenhängend ist eine schwächere Bedingung als lokal einfach zusammenhängend: Ein Kegel über den Hawaiischen Ohrringen ist semilokal einfach zusammenhängend, da sich jede Schleife über die Kegelspitze zusammenziehen lässt. Er ist aber (aus dem gleichen Grund wie die Hawaiischen Ohrringe selbst) nicht lokal einfach zusammenhängend.
Literatur
- Klaus Jänich: Topologie, 7-te Auflage. Springer 2001. ISBN 3-540-41284-0
- Munkres, James R.: Topology, Second Edition. Prentice Hall 2000, ISBN 0-13-181629-2
Weblinks
- Eric W. Weisstein: Connected Set auf MathWorld (englisch)
- Connected Set Eintrag der Springer Encyclopedia of Mathematics
Wikimedia Foundation.

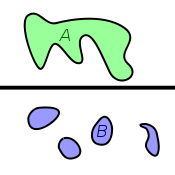
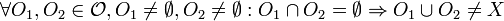
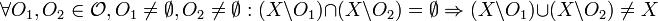

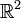 ist wegzusammenhängend, weil je zwei Punkte durch einen Weg verbunden sind.
ist wegzusammenhängend, weil je zwei Punkte durch einen Weg verbunden sind.