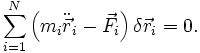- Virtuelle Verschiebung
-
Das d’Alembertsche Prinzip (nach Jean Baptiste le Rond d'Alembert) der klassischen Mechanik ermöglicht häufig das Aufstellen von Bewegungsgleichungen für Systeme der klassischen Dynamik, die Zwangskräften
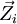 unterworfen sind. Es überträgt das Prinzip der virtuellen Arbeit der Statik[1]:
unterworfen sind. Es überträgt das Prinzip der virtuellen Arbeit der Statik[1]: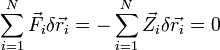
auf die Dynamik. Dabei denkt man sich das System in N Teilchen zerlegt (Index i), auf die die Zwangskräfte und die „eingeprägten“ äußeren Kräfte
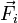 wirken (z. B. die Schwerkraft). Beim Übergang zur Dynamik betrachtet man formal das Kräftegleichgewicht:
wirken (z. B. die Schwerkraft). Beim Übergang zur Dynamik betrachtet man formal das Kräftegleichgewicht: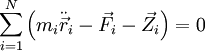
und bildet das Produkt mit den virtuellen Verschiebungen[2]
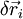 , wobei berücksichtigt wird, dass die Zwangskräfte selbst keine virtuelle Arbeit verrichten (das Skalarprodukt von Zwangskräften und virtuellen Verschiebungen also in diesem Fall verschwindet). Man erhält so das d’Alembertsche Prinzip (in der Formulierung von Lagrange):
, wobei berücksichtigt wird, dass die Zwangskräfte selbst keine virtuelle Arbeit verrichten (das Skalarprodukt von Zwangskräften und virtuellen Verschiebungen also in diesem Fall verschwindet). Man erhält so das d’Alembertsche Prinzip (in der Formulierung von Lagrange):In der Gleichung treten die Zwangskräfte nicht mehr auf – nur die äußeren Kräfte und die Trägheitskräfte. Die Zwangsbedingungen verstecken sich noch in den virtuellen Verschiebungen, was u. a. zur Folge hat, dass im Allgemeinen nur die Summe verschwindet und nicht jede Komponente der obigen Gleichung.
Um daraus Bewegungsgleichungen zu gewinnen, geht man bei
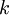 (holonomen) Zwangsbedingungen zu (bei N „Teilchen“) n = 3 N – k unabhängigen Koordinaten
(holonomen) Zwangsbedingungen zu (bei N „Teilchen“) n = 3 N – k unabhängigen Koordinaten 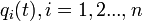 über und drückt alles durch diese neuen Lagekoordinaten aus („generalisierte Koordinaten“). Da die neuen Koordinaten sich unabhängig variieren lassen, ergeben sich die Bewegungsgleichungen aus dem Verschwinden der Koeffizienten von
über und drückt alles durch diese neuen Lagekoordinaten aus („generalisierte Koordinaten“). Da die neuen Koordinaten sich unabhängig variieren lassen, ergeben sich die Bewegungsgleichungen aus dem Verschwinden der Koeffizienten von 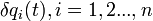 in den transformierten Gleichungen. Für holonome Zwangsbedingungen und konservative Kräfte (die sich aus einer Potentialfunktion ableiten lassen) ist das d’Alembert-Prinzip dann äquivalent zu den Lagrangegleichungen erster Art (siehe dort).
in den transformierten Gleichungen. Für holonome Zwangsbedingungen und konservative Kräfte (die sich aus einer Potentialfunktion ableiten lassen) ist das d’Alembert-Prinzip dann äquivalent zu den Lagrangegleichungen erster Art (siehe dort).Gelegentlich wird behauptet, das d’Alembertsche Prinzip wäre nur eine Umformung der Newtonschen Bewegungsgleichungen. Das übersieht aber wesentliche Vereinfachungen durch das Prinzip (wie die Elimination von Zwangskräften, die keine virtuelle Arbeit leisten) und kommt in den Worten von Georg Hamel fast einer Beleidigung von d’Alembert gleich[3].
Literatur
- Friedhelm Kuypers Klassische Mechanik, VCH, 5. Auflage 1997, ISBN 3-527-29269-1
- Georg Hamel Theoretische Mechanik, Springer 1967
Anmerkungen
- ↑ verwendet wird dabei, dass die Summe der Kräfte (aus Zwangskräften und äußeren Kräften) in der Statik verschwindet
- ↑ Infinitesimale Verschiebungen heissen virtuell, wenn sie mit den Zwangsbedingungen verträglich sind. Außerdem sollen sie instantan erfolgen (zu einer festen Zeit).
- ↑ Hamel Theoretische Mechanik, Springer 1967, S.220
Wikimedia Foundation.