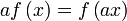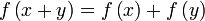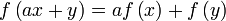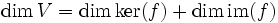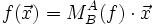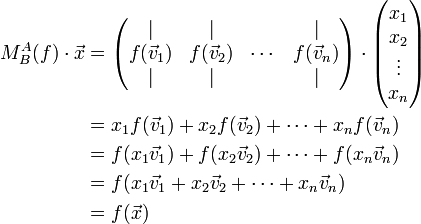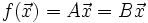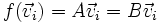- Vektorraumhomomorphismus
-
Die lineare Abbildung (auch linearer Operator) ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit eine Funktion zwischen zwei Vektorräumen, bei der es unerheblich ist, ob man zwei Vektoren zuerst addiert und dann deren Summe mittels der Funktion abbildet oder zuerst die Vektoren abbildet und dann die Summe der Bilder bildet. Gleiches gilt für die Multiplikation mit einem Skalar (z. B. einer reellen Zahl).
Das abgebildete Beispiel einer Spiegelung an der Y-Achse verdeutlicht dies. Der Vektor
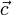 ist die Summe der Vektoren
ist die Summe der Vektoren 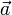 und
und 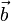 und sein Bild der Vektor
und sein Bild der Vektor 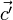 . Man erhält
. Man erhält 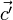 aber auch, wenn man die Bilder
aber auch, wenn man die Bilder 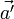 und
und 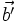 der Vektoren
der Vektoren 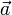 und
und 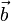 addiert.
addiert.Bei dieser Eigenschaft spricht man davon, dass eine lineare Abbildung mit den Vektorraum-Verknüpfungen Vektoraddition und skalarer Multiplikation verträglich ist. Es handelt sich somit bei der linearen Abbildung um einen Homomorphismus zwischen Vektorräumen.
In der Funktionalanalysis, bei der Betrachtung unendlichdimensionaler Vektorräume, die eine Topologie tragen, spricht man meist von linearen Operatoren statt von linearen Abbildungen. Formal gesehen sind die Begriffe synonym. Bei unendlichdimensionalen Vektorräumen ist jedoch die Frage der Stetigkeit bedeutsam, während Stetigkeit immer vorliegt bei linearen Abbildungen zwischen endlich-dimensionalen reellen Vektorräumen
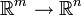 (jeweils mit der Euklidischen Norm) oder allgemeiner zwischen endlich-dimensionalen hausdorffschen topologischen Vektorräumen.
(jeweils mit der Euklidischen Norm) oder allgemeiner zwischen endlich-dimensionalen hausdorffschen topologischen Vektorräumen.Inhaltsverzeichnis
Formale Definition
Seien V und W Vektorräume über einem gemeinsamen Grundkörper K. Eine Abbildung
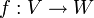 heißt lineare Abbildung, wenn für alle
heißt lineare Abbildung, wenn für alle 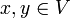 und
und 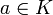 die folgenden Bedingungen gelten:
die folgenden Bedingungen gelten:- f ist homogen:
- f ist additiv:
Die zwei obigen Bedingungen kann man durch eine einzige ersetzen:Für y = 0V geht diese in die Bedingung für die Homogenität und für a = 1K in diejenige für die Additivität über.
Eine weitere, gleichwertige Bedingung ist die Forderung, dass der Graph der Abbildung f ein Untervektorraum der Summe der Vektorräume V und W ist.
Eigenschaften
Eine lineare Abbildung zwischen den Vektorräumen V und W bildet den Nullvektor von V auf den Nullvektor von W ab:
- f(0V) = 0W, da
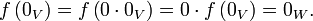
Bild und Kern
Zwei bei der Betrachtung linearer Abbildungen wichtige Mengen sind das Bild und der Kern einer linearen Abbildung
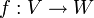 . Das Bild der Abbildung ist die Menge der Vektoren aus W, die f tatsächlich annimmt. Sie bilden einen Untervektorraum von W. Der Kern der Abbildung ist die Menge der Vektoren aus V, die durch f auf den Nullvektor von W abgebildet werden. Sie bilden einen Untervektorraum von V. Ist f injektiv, dann enthält der Kern nur den Nullvektor.
. Das Bild der Abbildung ist die Menge der Vektoren aus W, die f tatsächlich annimmt. Sie bilden einen Untervektorraum von W. Der Kern der Abbildung ist die Menge der Vektoren aus V, die durch f auf den Nullvektor von W abgebildet werden. Sie bilden einen Untervektorraum von V. Ist f injektiv, dann enthält der Kern nur den Nullvektor.Bild und Kern stehen über den Dimensionssatz in Bezug. Dieser sagt aus, dass die Dimension von V gleich der Summe der Dimensionen des Bildes und des Kerns ist:
Abbildungsmatrix
Hauptartikel: Abbildungsmatrix
Sind V und W endlichdimensionale Vektorräume, kann jede lineare Abbildung
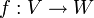 durch eine Matrix dargestellt werden. Deren Einträge hängen neben der Abbildung f nur von je einer frei wählbaren Basis
durch eine Matrix dargestellt werden. Deren Einträge hängen neben der Abbildung f nur von je einer frei wählbaren Basis 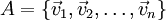 von V und
von V und 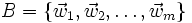 von W ab. Man bezeichnet sie als Abbildungsmatrix oder Darstellungsmatrix
von W ab. Man bezeichnet sie als Abbildungsmatrix oder Darstellungsmatrix 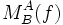 .
.Im Gegenzug legt auch jede Matrix eine lineare Abbildung fest:
Die Linearität der Abbildung f lässt sich anhand der Linearität von
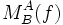 zeigen.
zeigen.Existenz
Um zu beweisen, dass die Darstellungsmatrix wirklich die lineare Abbildung f repräsentiert, führt man die Matrizenmultiplikation
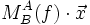 aus:
aus:Das dritte und vierte Gleichheitszeichen gilt wegen der zwei Eigenschaften der Linearität (der linearen Abbildung f).
Beim dritten Gleichheitszeichen benutzt man die homogene, beim vierten die additive Eigenschaft.
Eindeutigkeit
Auch die Eindeutigkeit der Darstellungsmatrix lässt sich auf einfache Weise zeigen. Sind A und B zwei Darstellungsmatrizen der linearen Abbildung f, so gilt
Setzt man in diese Gleichung einen beliebigen Basisvektor von V ein, erhält man
Da die Bilder
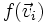 der Basisvektoren jedoch gerade die Spalten der Darstellungsmatrizen A und B sind, sind beide Matrizen identisch und es gibt somit nur eine Darstellungsmatrix der Abbildung f.
der Basisvektoren jedoch gerade die Spalten der Darstellungsmatrizen A und B sind, sind beide Matrizen identisch und es gibt somit nur eine Darstellungsmatrix der Abbildung f.Diagonalisierbarkeit
Eine lineare Abbildung
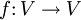 heißt diagonalisierbar, wenn eine Basis B von V existiert, sodass die Darstellungsmatrix
heißt diagonalisierbar, wenn eine Basis B von V existiert, sodass die Darstellungsmatrix 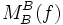 eine Diagonalmatrix ist.
eine Diagonalmatrix ist.Spezialfälle
- Monomorphismus
- Ein Monomorphismus zwischen Vektorräumen ist eine lineare Abbildung
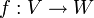 , die injektiv ist. Dies trifft genau dann zu, wenn die Spaltenvektoren der Darstellungsmatrix linear unabhängig sind.
, die injektiv ist. Dies trifft genau dann zu, wenn die Spaltenvektoren der Darstellungsmatrix linear unabhängig sind. - Epimorphismus
- Ein Epimorphismus zwischen Vektorräumen ist eine lineare Abbildung
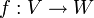 , die surjektiv ist. Dies trifft genau dann zu, wenn die Spaltenvektoren der Darstellungsmatrix ein Erzeugendensystem von W bilden.
, die surjektiv ist. Dies trifft genau dann zu, wenn die Spaltenvektoren der Darstellungsmatrix ein Erzeugendensystem von W bilden. - Isomorphismus
- Ein Isomorphismus zwischen Vektorräumen ist eine lineare Abbildung
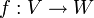 , die bijektiv ist. Dies trifft genau dann zu, wenn die Spaltenvektoren der Darstellungsmatrix eine Basis von W bilden. Die beiden Räume V und W bezeichnet man dann als isomorph.
, die bijektiv ist. Dies trifft genau dann zu, wenn die Spaltenvektoren der Darstellungsmatrix eine Basis von W bilden. Die beiden Räume V und W bezeichnet man dann als isomorph. - Endomorphismus
- Ein Endomorphismus zwischen Vektorräumen ist eine lineare Abbildung, bei der die Räume V und W gleich sind:
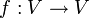 . Die Darstellungsmatrix dieser Abbildung ist eine quadratische Matrix.
. Die Darstellungsmatrix dieser Abbildung ist eine quadratische Matrix. - Automorphismus
- Ein Automorphismus zwischen Vektorräumen ist eine bijektive lineare Abbildung, bei der die Räume V und W gleich sind. Er ist also sowohl ein Isomorphismus als auch ein Endomorphismus. Die Darstellungsmatrix dieser Abbildung ist eine reguläre Matrix.
Vektorraum der linearen Abbildungen
Die linearen Abbildungen bilden zusammen mit dem Grundkörper K einen Vektorraum. Das bedeutet, dass die Summe zweier linearer Abbildungen f und g, komponentenweise definiert durch
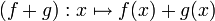 , wieder eine lineare Abbildung ist. Ebenso ist das Produkt
, wieder eine lineare Abbildung ist. Ebenso ist das Produkt 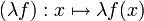 einer linearen Abbildung mit einem Skalar
einer linearen Abbildung mit einem Skalar 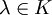 wieder linear.
wieder linear.Algebra der linearen Abbildungen
Betrachten wir die Menge der linearen Selbstabbildungen auf einem Vektorraum. Diese bilden selber wieder einen Vektorraum. Mit der Verkettung von Abbildungen bilden sie eine assoziative Algebra.
Verallgemeinerung
Eine lineare Abbildung ist ein Spezialfall einer affinen Abbildung.
Literatur
- Detlef Wille: Repetitorium der Linearen Algebra Teil 1. 4. Auflage. Binomi, Springe 2003, ISBN 3-923923-40-6
- Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 6. Auflage, Vieweg, ISBN 3-528-56508-X, S. 124–143
- f ist homogen:
Wikimedia Foundation.