Unterobjekt

Monomorphismus ist ein Begriff aus den mathematischen Teilgebieten der Algebra und der Kategorientheorie. In der Algebra bezeichnet er einen Homomorphismus, der injektiv ist. In der Kategorientheorie verallgemeinert er den Begriff der injektiven Abbildung und erlaubt es Objekte als Unterobjekte von anderen aufzufassen.

Man beachte, dass die universelle Algebra und die Kategorientheorie jeweils einen zu Monomorphismus dualen Begriff, nämlich den Epimorphismus, erklären, diese beiden Epimorphismus-Begriffe jedoch nicht äquivalent sind.

Monomorphismen algebraischer Strukturen

Ein Homomorphismus von

• Vektorräumen oder allgemeiner Moduln
• oder (abelschen) Gruppen
• oder Ringen oder Körpern
• oder allgemein algebraischen Strukturen,

der injektiv ist, heißt Monomorphismus.

Beispiele

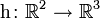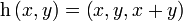• Die Abbildung $\operatorname h\colon\mathbb{R}^2\to\mathbb{R}^3$ mit $\operatorname h\left(x,y\right)=\left(x,y,x+y\right)$ ist ein Vektorraum-Monomorphismus.
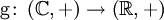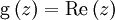• Die Abbildung $\operatorname g\colon\left(\mathbb{C},+\right)\to\left(\mathbb{R},+\right)$ mit $\operatorname g\left(z\right) = \operatorname{Re}\left(z\right)$ ist zwar ein Gruppen-Homomorphismus, aber nicht injektiv.
• Ein Homomorphismus von Gruppen, Ringen oder Moduln (insbesondere Vektorräumen) ist genau dann injektiv, wenn sein Kern trivial ist. Für einen beliebigen Homomorphismus 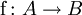$\operatorname f\colon A\to B$ von Gruppen, Ringen oder Moduln (bzw. Vektorräumen) ist
      $\tilde \operatorname f\colon A/{\ker \operatorname f}\to B$
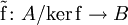
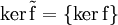  ein Monomorphismus, wenn $\operatorname{\tilde f}\colon [a]\mapsto \operatorname f(a)$ die kanonische Abbildung auf der Restklassenstruktur ist. Denn es gilt $\ker \operatorname{\tilde f} = \lbrace \ker \operatorname f \rbrace$ und damit ist 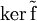$\ker \operatorname{\tilde f}$ trivial.
• Homomorphismen von Körpern sind stets injektiv.

Monomorphismen in beliebigen Kategorien

In der Kategorientheorie ist ein Monomorphismus ein Morphismus 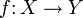$f\colon X\to Y$ mit folgender Eigenschaft:

Sind 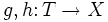$g,h\colon T\to X$ beliebige Morphismen mit 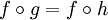$f\circ g=f\circ h$, dann folgt g = h (Man sagt auch: f ist links kürzbar).

X (zusammen mit f) heißt dann ein Unterobjekt von Y.

In Kategorien von algebraischen Strukturen sowie in den Kategorien der Mengen oder der topologischen Räume sind die Monomorphismen genau die injektiven Morphismen. Es gibt aber auch konkrete Kategorien mit nicht-injektiven Monomorphismen.

Beispiel eines nicht injektiven Monomorphismus

Wir betrachten die Kategorie Div der teilbaren Gruppen: Die Objekte sind die abelschen Gruppen G, für die folgendes gilt:

Für alle a in G und alle n in N, n > 0, existiert ein b in G mit a = nb; das Element a lässt sich also "durch n teilen".

Die Morphismen sind die Gruppenhomomorphismen zwischen diesen Gruppen.

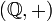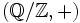Die abelschen Gruppen $(\mathbb{Q}, +)$ und $(\mathbb{Q} / \mathbb{Z}, +)$ liegen in dieser Kategorie. Die kanonische Projektion 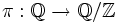$\pi: \mathbb{Q} \to \mathbb{Q} / \mathbb{Z}$ ist surjektiv, aber nicht injektiv. Wir zeigen, dass sie ein Monomorphismus in Div ist. Sei dazu X irgendeine teilbare Gruppe und 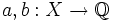$a, b: X \to \mathbb{Q}$ zwei Morphismen mit der Eigenschaft 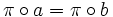$\pi \circ a = \pi \circ b$. Dies bedeutet, dass für jedes Element x von X gilt: 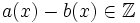$a(x) - b(x) \in \mathbb{Z}$. Wäre nun 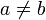$a \neq b$, dann gäbe es ein x in X mit 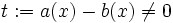$t:=a(x)-b(x)\neq 0$. Falls t < 0 ist, vertausche die Rollen von a und b, so dass im folgenden t > 0 ist. Da X teilbar ist, gibt es ein y in X mit 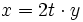$x = 2t\cdot y$. Dann ist aber

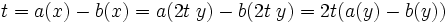$t = a(x)-b(x) = a(2t\;y)-b(2t\;y) = 2t(a(y)-b(y))$, also a(y) − b(y) = 1 / 2,

und das ist ein Widerspruch zur Ganzheit der Differenz von a und b.

Spezielle Monomorphismen

Ein Monomorphismus f heißt extremal, wenn er zusätzlich folgende Extremaleigenschaft erfüllt:

Ist f= g o m, und m ist ein Epimorphismus, dann muss m ein Isomorphismus sein.

In den Kategorien Set und Grp sind die extremalen Monomorphismen gerade die Monomorphismen.

In der Kategorie Top sind die extremalen Monomorphismen die Einbettungen (bis auf Homöomorphismus). In der Kategorie Top₂ sind die extremalen Monomorphismen die abgeschlossenen Einbettungen (bis auf Homöomorphismen).

In der Kategorie BanSp₁ sind die extremalen Monomorphismen genau diejenigen linearen stetigen injektiven Abbildungen f, für die es ein positives m gibt so dass für alle x aus dem Definitionsbereich gilt:

$m||x||\leq ||f(x)||$

Siehe auch

• Isomorphismus