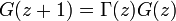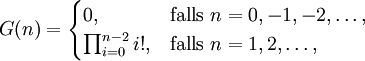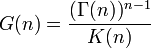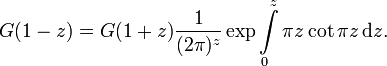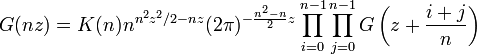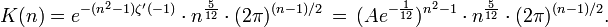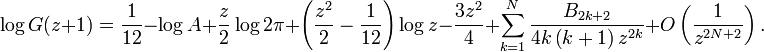- Barnes'sche G-Funktion
-
Die Barnessche G-Funktion, typischerweise mit G(z) bezeichnet, ist eine Funktion, die eine Erweiterung der Superfakultäten auf die komplexen Zahlen darstellt. Sie steht in Beziehung zur Gammafunktion, der K-Funktion und der Konstanten von Glaisher-Kinkelin und ist nach dem Mathematiker Ernest William Barnes benannt.[1]
Formal ist die Barnessche G-Funktion in der Form eines Weierstraß-Produkts definiert als
wobei γ die Euler-Mascheroni-Konstante bezeichnet.
Inhaltsverzeichnis
Differenzengleichung, Funktionalgleichung und spezielle Werte
Die Barnessche G-Funktion erfüllt die Differenzengleichung
mit der Normierung G(1) = 1. Die Differenzengleichung impliziert, dass G die folgenden Werte für ganzzahlige Argumente annimmt:
so dass
wo Γ(n) die Gammafunktion und K(n) die K-Funktion bezeichnen. Die Differenzengleichung definiert die G-Funktion eindeutig, wenn die Konvexitätsbedingung
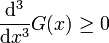 gestellt wird.[2]
gestellt wird.[2]Die Differenzengleichung der G-Funktion und die Funktionalgleichung der Gamma-Funktion liefern die folgende Funktionalgleichung für die G-Funktion, wie ursprünglich von Hermann Kinkelin bewiesen wurde:
Multiplikationsformel
Wie die Gamma-Funktion erfüllt auch die G-Funktion eine Multiplikationsformel:[3]
wobei K(n) eine Funktion ist, die durch
gegeben ist. Hierbei ist
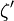 die Ableitung der Riemannschen Zeta-Funktion und A die Konstante von Glaisher-Kinkelin.
die Ableitung der Riemannschen Zeta-Funktion und A die Konstante von Glaisher-Kinkelin.Asymptotische Entwicklung
Die Funktion
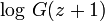 hat die folgende asymtotische Entwicklung, die von Barnes gefunden wurde:
hat die folgende asymtotische Entwicklung, die von Barnes gefunden wurde:Hierbei bezeichnet Bk die Bernoulli-Zahlen und A die Konstante von Glaisher-Kinkelin. (Man beachte, dass zur Zeit von Barnes[4] die Bernoulli-Zahl B2k als ( − 1)k + 1Bk geschrieben wurde. Diese Konvention wird nicht länger verwendet.) Die Entwicklung ist gültig für z in jedem Sektor, der nicht die negative reelle Achse enthält.
Weblink
- Eric W. Weisstein: Barnes G-Function auf MathWorld (englisch)
Einzelnachweise
- ↑ E.W.Barnes: The theory of the G-function. In: Quarterly Journ. Pure and Appl. Math. Band 31, 1900, Seiten 264-314.
- ↑ M. F. Vignéras: L'équation fonctionelle de la fonction zêta de Selberg du groupe modulaire
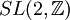 . In: Astérisque Band 61, 1979, Seiten 235-249.
. In: Astérisque Band 61, 1979, Seiten 235-249. - ↑ I. Vardi: Determinants of Laplacians and multiple gamma functions. In: SIAM J. Math. Anal. Band 19, 1988, Seiten 493-507.
- ↑ E. T. Whittaker, G. N. Watson: A Course of Modern Analysis. Cambridge University Press, ISBN 978-0521091893.
Wikimedia Foundation.

![G(z+1)=(2\pi)^{z/2} e^{-[z(z+1)+\gamma z^2]/2}\prod_{n=1}^\infty \left[\left(1+\frac{z}{n}\right)^ne^{-z+z^2/(2n)}\right]](/pictures/dewiki/98/bcc0d5c820483a6b2a27749af185becc.png)