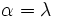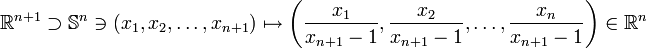Stereographische Projektion

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Projektion einer Kugeloberfläche in eine Ebene (Prinzip)

Stereografische Projektion in der Fotografie

Die stereografische Projektion (auch konforme azimutale Projektion) ist ein winkeltreues (konformes) Abbildungsverfahren zum mathematischen Entwurf von Kartennetzen. Die Projektion der Erdkugel erfolgt auf eine Tangentialebene, wobei das Projektionszentrum jener Punkt ist, der dem Berührungs- oder Hauptpunkt der geplanten Landkarte gegenüber liegt.

Die Projektion hat neben ihrer Winkeltreue auch die Eigenschaft der Kreistreue, verzerrt allerdings weiter entfernte Strecken erheblich. Sie findet ihre häufigste Verwendung nicht in der Geographie, sondern in der Astronomie (Sternkarten, Planeten), in der Geodäsie und Navigation (winkeltreue Karten) und in der Geophysik (Verteilung von Kräften oder Linienstrukturen auf der Erdkugel). In der Mathematik ist sie die Abbildung zwischen der komplexen Zahlenebene und der Riemannschen Zahlenkugel.

Grundlagen

Stereografische Projektion, normale Lage

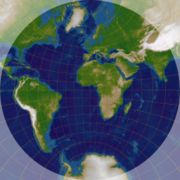
Bei diesem Kartennetzentwurf werden Orthodrome (Abschnitte der Großkreise) nicht als Gerade, sondern gekrümmt dargestellt. Sie besitzen allerdings – wie alle anderen Kreise auch – exakte Kreisform. Die Meridiane werden in der Abbildung daher zu Kreisen mit relativ großem Radius, die durch die Abbildung des Nord- und Südpols gehen (bei Landkarten weit außerhalb des Kartenblattes). Nur bei der polaren stereografischen Projektion (z. B. für Flugkarten der Arktis) werden die Meridiane zu Geraden durch den Nordpol (siehe Bild unten links).

Die Abbildungsgleichung ist für das Azimut (Richtung vom Haupt- zum jeweiligen Kartenpunkt)

$\mathbf{\alpha = \lambda }$

(wobei im Fall der polaren Projektion der Winkel λ die geografische Länge selbst ist, und für den Abstand m des Kartenpunktes

$m = 2 \cdot r \cdot \tan \frac{\delta}{2}$.

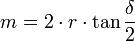Der Kartennetzentwurf lässt sich mit Hilfe von Zirkel und Lineal ausführen, was ein zweiter Grund für seine vielfache Verwendung seit der Antike ist. Er kann theoretisch die gesamte Erdoberfläche abbilden, mit Ausnahme des Projektionszentrums, welches als Gegenpol ins Unendliche projiziert wird.

Anwendung

Die Flächenverzerrung nimmt mit zunehmender Entfernung vom Berührungspunkt (Hauptpunkt) stark zu. Im Allgemeinen beschränkt man die Abbildung daher auf maximal eine Halbkugel. Da die Abbildung winkeltreu ist und Kreise wieder als solche abbildet, ist die stereografische Projektion z. B. gut für Sternkarten geeignet.

 

Polare stereografische Projektion		Transversale stereografische Projektion
	Falls man die Nordhalbkugel abbilden will, liegt das Projektionszentrum im Südpol der Erde.		Das Projektionszentrum – und damit der Berührungspunkt ebenso – liegt nicht im Pol, sondern auf dem Äquator. Der hervorgehobene Teil entspricht genau der Halbkugel von 90° West bis 90° Ost.

Verallgemeinerung für höherdimensionale Räume

Die oben beschriebene Projektion ist der Spezialfall der allgemeinen stereografischen Projektion: Im dreidimensionalen Raum 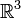$\mathbb{R}^{3}$ wird die zweidimensionale Kugeloberfläche 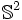$\mathbb{S}^{2}$, (2-Sphäre), auf die Kartenebene und somit in den zweidimensionalen Raum 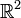$\mathbb{R}^{2}$ abgebildet.

Im (n + 1)-dimensionalen Raum 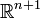$\mathbb{R}^{n+1}$ kann man die auf der n-Sphäre 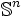$\mathbb{S}^{n}$ gelegenen Punkte mit den Koordinaten 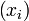$\left(x_i\right)$ z.B. mittels der folgenden Formel in den $\mathbb{R}^{n}$ abbilden:

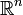$\mathbb{R}^{n+1} \supset \mathbb{S}^{n} \ni \left(x_1, x_2, \ldots, x_{n+1}\right) \mapsto \left(\frac{x_1}{x_{n+1}-1}, \frac{x_2}{x_{n+1}-1}, \ldots, \frac{x_n}{x_{n+1}-1}\right) \in \mathbb{R}^n$

Die Karte aus diesem Beispiel ist für x_{n + 1} = 1, genannt der Nordpol, natürlich nicht definiert. Betrachtet man die Karte mit x_{n + 1} + 1 statt x_{n + 1} − 1, dann wird die Sphäre bis auf den Südpol abgebildet. Man hat also einen möglichen Atlas gefunden. Dies zeigt damit auch, dass die n-Sphäre eine n-dimensionale Mannigfaltigkeit ist.

Die stereografische Projektion der Polfigur eines Diamantgitters in [111]-Richtung zeigt die dreizählige Symmetrie der Raumdiagonalen.

Weitere Anwendungen

stereografische Projektion mit den {100}-Ebenen (grün), den {110}-Ebenen (blau) und den {111}-Ebenen (rot) einer kubischen Struktur (willkürliche Orientierung)

Praktische Anwendung findet die stereografische Projektion in der Kristallographie bei der Bestimmung der Orientierung der Gitterebenen eines Kristalls (Laue-Verfahren). Bei der stereografischen Projektion liegt die Projektionsfläche in der Äquatorebene der Kugel. Der Punkt, an dem die Flächennormale eines Kristalles, welche auch durch den Mittelpunkt der Kugel geht, die Kugeloberfläche durchstößt, wird mit dem Pol der gegenüberliegenden Kugelsphäre verbunden. Der Schnittpunkt dieser letzteren Gerade mit der Äquatorebene ist der Projektionspunkt.

Erläuterungen zum Bild:
Am Beispiel eines Würfels (Kubisches Gitter) mag man sich die gezeigten Ebenen vorstellen. Legt man an die Kanten eines Würfels Richtungsanzeiger (Vektoren), so lassen sich diese mit den Koordinaten (1;0;0), (0;1;0) und (0;0;1) beschreiben. Eine Ebene, auf der eine dieser Würfelkanten senkrecht steht, sich also in die gleiche Richtung erstreckt wie eine beliebige Würfelfläche ist eine {100}-Ebene. Eine Ebene senkrecht zu einer beliebigen Flächendiagonale mit Richtungsanzeiger (1;1;0), (1;-1;0), (0;1;1), (0;1;-1), (1;0;1) oder (-1;0;1) gehört dann zu den {110}-Ebenen und schließlich: Eine Ebene, die senkrecht auf einer der vier Raumdiagonalen (1;1;1), (-1;1;1), (1;-1;1) oder (1;1;-1) liegt, ist eine {111}-Ebene. Genaueres zu den Bezeichnungen der Ebenen siehe Millersche Indizes.

Siehe auch

• Planisphäre und Sternkarte
• Kartennetzentwurf
• Universale Polare Stereografische Projektion
• Fischaugenobjektiv
• Riemannsche Zahlenkugel

Literatur

Quellen für die mathematischen Erläuterungen:

• Königsberger: Analysis 2. 1. Auflage. Springer-Verlag 1993. ISBN 3-540-54723-1

Allgemeine Beschreibung n-dim. Sphäre: Abschnitt 1.3.II, konformität: Abschnitt 3.1

• Scheja/Storch: Lehrbuch der Algebra, Teil 1. 2.Auflage. Teubner Stuttgart 1994. ISBN 3-519-12203-0

Projektive Darstellung: Abschnitt V.H Bsp. 4

Weblinks

• Interaktive dreidimensionale Darstellung der stereografischen Projektion mittels Java-Applet (englisch)
• Vergleich verschiedener Projektionen (englisch)