- Singulärwert-Zerlegung
-
Die Singulärwertzerlegung (Abk.: SVD für Singular Value Decomposition) einer Matrix bezeichnet deren Darstellung als Produkt dreier spezieller Matrizen. Daraus kann man die Singulärwerte der Matrix ablesen. Diese charakterisieren, ähnlich den Eigenwerten, Eigenschaften der Matrix. Singulärwerte kann man für jede Matrix bestimmen, im Gegensatz zu den Eigenwerten auch bei nichtquadratischen.
Inhaltsverzeichnis
Definition
Als Singulärwertzerlegung einer komplexen Matrix
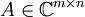 mit Rang r bezeichnet man das Produkt
mit Rang r bezeichnet man das Produkt- A = UΣV *
aus der unitären Matrix
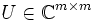 , der Adjungierten V * der unitären Matrix
, der Adjungierten V * der unitären Matrix 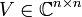 und der reellen
und der reellen 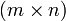 -Matrix
-MatrixDie Einträge σi von Σ sind die Singulärwerte von A. Für sie gilt
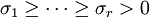 .
.
Eigenschaften
Jede Matrix besitzt eine Singulärwertzerlegung. Bei einer reellen Matrix können die Matrizen U und V der Singulärwertzerlegung reell gewählt werden.
Wegen
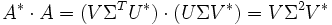 ist
ist  ähnlich zu Σ2. Damit sind die Singulärwerte der Matrix A gleich den Quadratwurzeln aus den Eigenwerten von A * A. Also ist die Spektralnorm von A gleich σ1.
ähnlich zu Σ2. Damit sind die Singulärwerte der Matrix A gleich den Quadratwurzeln aus den Eigenwerten von A * A. Also ist die Spektralnorm von A gleich σ1.Einsetzen und Nachrechnen zeigt, dass sich die Pseudoinverse (bei Invertierbarkeit die Inverse) zu A aus
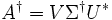 mit
mit 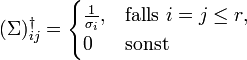 ergibt. Somit sind die Singulärwerte der Inversen zu A genau
ergibt. Somit sind die Singulärwerte der Inversen zu A genau  , und die Konditionszahl (bezogen auf die Spektralnorm) von A ergibt sich zu
, und die Konditionszahl (bezogen auf die Spektralnorm) von A ergibt sich zu 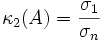 .
.Da unitäre Transformationen den Betrag der Determinante nicht ändern, gilt
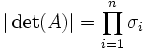 für n = m.
für n = m.Numerische Bestimmung der Singulärwertzerlegung
Da die Singulärwerte mit den Eigenwerten der Matrix A * A zusammenhängen, wäre ein naheliegender Algorithmus zur numerischen Bestimmung einer Singulärwertzerlegung der Matrix die numerische Lösung des symmetrischen Eigenwertproblems zu A * A. Allerdings ist ein solcher Algorithmus numerisch instabil und zudem aufgrund der benötigten Matrix-Matrix-Produkte auch sehr aufwändig.
In den 1960er entwickelte vor allem Gene Golub stabile direkte und iterative Algorithmen zur Berechnung einer Singulärwertzerlegung, womit die Zerlegung praktisch nutzbar wurde. Das direkte Verfahren wurde 1965 mit Kahan und das iterative 1970 mit Christian Reinsch veröffentlicht. Die Verfahren formen zunächst die Matrix A in eine günstigere Gestalt um: Mit Hilfe von orthogonalen Transformationen (etwa durch Householder-Transformationen) wird die Matrix A auf Bidiagonalform B gebracht. Diese umgeformte Matrix erlaubt dann durch eine modifizierte Form des QR-Algorithmus eine effiziente Bestimmung der Singulärwerte. Der Aufwand liegt bei ca.
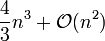 arithmetischen Operationen.
arithmetischen Operationen.Anwendung
Dieses Verfahren wird insbesondere in der numerischen Mathematik verwendet. Dort lassen sich beispielsweise quasisinguläre lineare Gleichungssysteme im Rahmen rechentechnischer Genauigkeiten passabel lösen.
Einige moderne Bildkompressionsverfahren beruhen auf einem Algorithmus, der das Bild (=Matrix aus Farbwerten) in eine SVD überführt und anschließend nur die stark von null verschieden Elemente der Matrix Σ berücksichtigt und dann die zur Rückgewinnung der Matrix erforderlichen Vektoren sowie die verbliebenen Diagonalelemente speichert. Besonders effektiv ist diese Kompression bei bestimmten rechteckigen Mustern und natürlich, je größer (und je quadratischer) das Bild ist. Dies ist eine mögliche Anwendung von Modellreduktion. Das Weglassen von kleinen Singulärwerten ist ein verlustbehaftetes Modellreduktionsverfahren.
In der Teilchenphysik benutzt man die Singulärwertzerlegung, um Massenmatrizen von Dirac-Teilchen zu diagonalisieren. Die Singulärwerte geben die Massen der Teilchen in ihren Masseneigenzuständen an. Aus den Transformationsmatrizen U und V konstruiert man Mischungsmatrizen wie die CKM-Matrix, die ausdrücken, dass die Masseneigenzustände von Teilchen aus einer Mischung von Flavoreigenzuständen bestehen können.
Literatur
- Günter Gramlich: Anwendung der Linearen Algebra mit MATLAB®. Carl Hanser Verlag, 2004. ISBN 3-446-22655-9
- Peter Deuflhard und Andreas Hohmann: Numerische Mathematik I. Walter deGruyter, Berlin, 2000.
Weblinks
Wikimedia Foundation.


