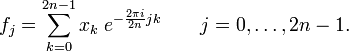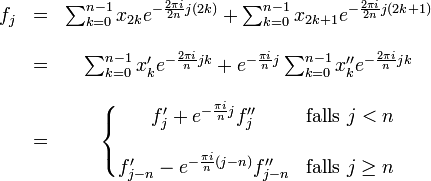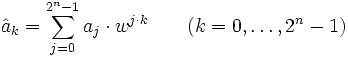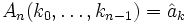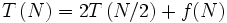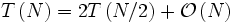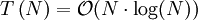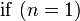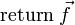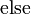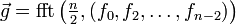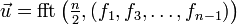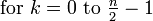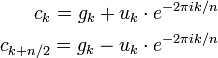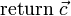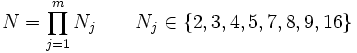- Schnelle Fouriertransformation
-
Die schnelle Fourier-Transformation (englisch fast Fourier transform, daher meist FFT abgekürzt) ist ein Algorithmus zur effizienten Berechnung der Werte einer diskreten Fourier-Transformation (DFT). Bei dem Algorithmus handelt es sich um ein klassisches Teile-und-herrsche-Verfahren. Im Gegensatz zur direkten Berechnung verwendet die schnelle Fourier-Transformation zuvor berechnete Zwischenergebnisse und spart arithmetische Rechenoperationen ein. Das Verfahren wird James Cooley und John W. Tukey zugeschrieben, die es 1965 veröffentlichten. Genau genommen wurde eine Form des Algorithmus bereits 1805 von Carl Friedrich Gauß entworfen, der ihn zur Berechnung der Flugbahnen der Asteroiden Pallas und Juno verwendete. Darüber hinaus wurden eingeschränkte Formen des Algorithmus mehrfach vor Cooley und Tukey entwickelt, so z. B. von Irving John Good (1960). Nach Cooley und Tukey hat es darüber hinaus zahlreiche Verbesserungsvorschläge und Variationen gegeben, so etwa von Georg Bruun, C. M. Rader und Leo I. Bluestein.
Analog gibt es für die diskrete inverse Fourier-Transformation einen schnellen Algorithmus (inverse FFT – iFFT). Es kommen bei der iFFT identische Algorithmen mit anderen Koeffizienten in der Berechnung zur Anwendung.
Inhaltsverzeichnis
Informelle Beschreibung des Algorithmus (Cooley und Tukey)
Der Algorithmus von Cooley und Tukey ist ein klassisches Teile-und-herrsche-Verfahren. Voraussetzung für seine Anwendung ist, dass die Anzahl der Stützstellen bzw. Abtastpunkte eine Zweierpotenz ist. Da die Anzahl solcher Punkte im Rahmen von Messverfahren jedoch im Allgemeinen frei gewählt werden kann, handelt es sich dabei nicht um eine gravierende Einschränkung. Das Problem der Berechnung einer DFT der Größe 2n wird nun zunächst in zwei Berechnungen der DFT der Größe n aufgeteilt – der Vektor der Messwerte wird in die Teilvektoren der Einträge zu geraden bzw. ungeraden Indizes aufgeteilt und von beiden die DFT bestimmt. Die beiden Teilergebnisse werden dann wieder zu einem Gesamtergebnis zusammengefügt. Zur Berechnung der beiden Hälften werden die Eigenschaften der Einheitswurzeln aus der Fouriermatrix ausgenutzt. Eine rekursive Anwendung dieser Grundidee ermöglicht schließlich eine Berechnung in
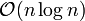 Zeit.
Zeit.Formelle Beschreibung des Algorithmus (Cooley und Tukey)
Zunächst sei in Erinnerung gerufen, dass die DFT der Größe 2n durch folgende Formel definiert ist:
Notieren wir die Einträge zu geraden Indizes als
- x'0 = x0, x'1 = x2, …, x'n-1 = x2n-2
und bezeichnen deren Transformierte nach DFT der Größe n mit
- f'0, …, f'n-1;
die Einträge zu ungeraden Indizes notieren wir entsprechend als
- x"0 = x1, x"1 = x3, …, x"n-1 = x2n-1
und bezeichnen deren Transformierte nach DFT der Größe n mit
- f"0, …, f"n-1.
Dann folgt:
Mathematische Beschreibung (allgemeiner Fall)
In der Mathematik wird die schnelle diskrete Fouriertransformation in einem wesentlich allgemeineren Kontext behandelt:
Sei R ein kommutativer unitärer Ring. In R sei die Zahl 2 = 1 + 1 eine Einheit (d. h. invertierbar); ferner sei
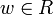 eine 2n-te Einheitswurzel mit
eine 2n-te Einheitswurzel mit 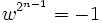 . Zum Beispiel ist im Restklassenring
. Zum Beispiel ist im Restklassenring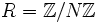 mit
mit 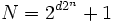 ,
, 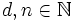 , d ungerade (das ist gleichbedeutend mit der Forderung „teilerfremd zu 2n“),
, d ungerade (das ist gleichbedeutend mit der Forderung „teilerfremd zu 2n“),
das Element w = 22d eine solche Einheitswurzel, die entsprechende FFT wird im Schönhage-Strassen-Algorithmus verwendet.
Dann lässt sich im Modul
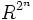 zu
zu 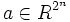 die diskrete Fouriertransformierte
die diskrete Fouriertransformierte 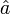 mit
mitwie folgt optimiert berechnen:
Zunächst stellen wir die Indizes j und k wie folgt dual dar:
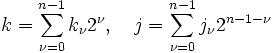 .
.
Damit haben wir folgende Rekursion:
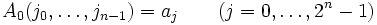 ,
,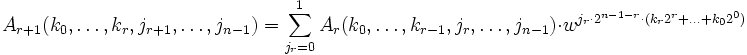 .
.
Wegen
erhalten wir hieraus die diskrete Fouriertransformierte
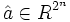 .
.Komplexität
Die FFT ist im Gegensatz zur DFT nur möglich, wenn die Länge des Eingangsvektors einer Zweierpotenz entspricht (zumindest gilt dies für die sogenannte klassische Variante der FFT, wie sie oben definiert wurde). Die Anzahl der Abtastpunkte kann also beispielsweise 1, 2, 4, 8, 16, 32 usw. betragen. Man spricht hier von einer Radix-2-FFT.
Aus obiger Rekursion ergibt sich folgende Rekursionsgleichung:
Hierbei beschreibt der Term f(N) den Aufwand, um die Ergebnisse mit einer Potenz der Einheitswurzel zu multiplizieren und die Ergebnisse zu addieren. Es werden Zahlen der Länge n addiert. Zahlen der Länge n/2 werden mit Einheitswurzeln (von fester Länge) multipliziert. Insgesamt ist f(N) also linear beschränkt:
Mit dem Master Theorem ergibt sich eine Laufzeit von:
Die Struktur des Datenflusses kann durch einen Schmetterlingsgraphen beschrieben werden, der die Reihenfolge der Berechnung festlegt.
Implementierung (Pseudocode)
Die Implementierung erfolgt durch einen rekursiven Algorithmus. Das Feld mit den Messwerten wird als Parameter übergeben und solange in zwei Felder mit geradem bzw. ungeradem Index aufgeteilt, bis es nur noch aus einem Element besteht (Rekursionsabbruch). In jedem Rekursionsdurchlauf wird eine Schleife bis zur halben Länge des Feldes durchlaufen, da mit jedem Schleifendurchlauf gleich zwei Feldelemente berechnet werden können (siehe Komplexität).
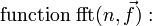
Alternative Formen der FFT
Neben dem oben dargestellten FFT-Algorithmus von Cooley und Tukey, auch Radix-2-Algorithmus genannt, existieren noch eine Reihe weiterer Algorithmen zur schnellen Fourier-Transformation. Die Varianten unterscheiden sich darin, wie bestimmte Teile des „naiven“ Algorithmus so umgeformt werden, dass weniger (Hochpräzisions-)Multiplikationen notwendig sind. Dabei gilt meist, dass die Reduktion in der Anzahl der Multiplikationen eine erhöhte Anzahl von Additionen sowie von gleichzeitig im Speicher zu haltenden Zwischenergebnissen hervorruft.
Im Folgenden sind übersichtsartig einige weitere Algorithmen dargestellt. Details und genaue mathematische Beschreibungen samt Herleitungen finden sich in der unten angegebenen Literatur.
Radix-4-Algorithmus
Der Radix-4-Algorithmus ist, analog dazu der Radix-8-Algorithmus oder allgemein Radix-2N-Algorithmus, eine Weiterentwicklung des obigen Radix-2-Algorithmus. Der Hauptunterschied besteht darin, dass die Anzahl der zu verarbeitenden Datenpunkte eine Potenz von 4 bzw. 4N darstellen muss. Die Verarbeitungstruktur bleibt dabei gleich, nur dass in dem Schmetterlingsgraph pro Element statt zwei Datenpfade vier bzw. acht und allgemein 4N Datenpfade miteinander verknüpft werden müssen. Der Vorteil besteht in einem weiter reduzierten Rechenaufwand und damit Geschwindigkeitsvorteil. So sind, verglichen mit dem obigen Algorithmus von Cooley und Tukey, bei dem Radix-4-Algorithmus ca. 25 % weniger Multiplikationen notwendig. Bei dem Radix-8-Algorithmus reduziert sich die Anzahl der Multiplikationen um ca. 40 %.
Nachteil dieser Verfahren ist die gröbere Struktur und ein aufwendiger Programmcode. So lassen sich mit Radix-4-Algorithmus nur Blöcke der Längen 4, 16, 64, 256, 1024, 4096, … verarbeiten. Bei dem Radix-8-Algorithmus sind die Einschränkungen analog zu sehen. Wäre in einer bestimmten Anwendung eine Blocklänge von beispielsweise 2048 Stützstellen ideal und damit auch der Speicherplatz gering zu halten, können diese schnelleren Algorithmen daher nicht eingesetzt werden. Es müsste dann ein größerer Speicher eingesetzt werden und der Rechenaufwand gesteigert werden.
Winograd-Algorithmus
Bei diesem Algorithmus ist nur eine bestimmte, endliche Anzahl von Stützstellen der Anzahl N möglich, nämlich:
wobei alle Kombinationen von Nj zulässig sind, bei denen die verwendeten Nj relativ prim sind. Dadurch ist nur eine maximale Blocklänge von 5040 möglich. Die möglichen Werte für N liegen aber in dem Bereich bis 5040 dichter auf der Zahlengeraden als die Zweierpotenzen. Es ist damit eine bessere Feinabstimmung der Blocklänge möglich. Aufgebaut wird der Algorithmus aus Basisblöcken der DFT, deren Längen mit Nj korrespondieren. Bei diesem Verfahren wird zwar die Anzahl der Multiplikationen gegenüber dem Radix-2-Algorithmus reduziert, gleichzeitig steigt aber die Anzahl der notwendigen Additionen. Außerdem ist am Eingang und Ausgang jeder DFT eine aufwendige Permutation der Daten notwendig, die nach den Regeln des Chinesischen Restsatzes gebildet wird.
Diese Art der schnellen Fourier-Transformation besitzt in praktischen Implementierungen dann Vorteile gegenüber der Radix-2-Methode, wenn der für die FFT verwendete Mikrocontroller keine eigene Multipliziereinheit besitzt und für die Multiplikationen sehr viel Rechenzeit aufgewendet werden muss. In heutigen Signalprozessoren mit eigenen Multipliziereinheiten hat dieser Algorithmus keine wesentliche Bedeutung mehr.
Primfaktor-Algorithmus
Dieser FFT-Algorithmus basiert auf ähnlichen Ideen wie der Winograd-Algorithmus, allerdings ist die Struktur einfacher und damit der Aufwand an Multiplikationen höher als beim Winograd-Algorithmus. Der wesentliche Vorteil bei der Implementierung liegt in der effizienten Ausnutzung des zur Verfügung stehenden Speichers durch optimale Anpassung der Blocklänge. Wenn in einer bestimmten Anwendung zwar eine schnelle Multipliziereinheit verfügbar ist und gleichzeitig der Speicher knapp, kann dieser Algorithmus optimal sein. Die Ausführungszeit ist bei ähnlicher Blocklänge mit der des Algorithmus von Cooley und Tukey vergleichbar.
Goertzel-Algorithmus
Der Goertzel-Algorithmus stellt eine besondere Form zur effizienten Berechnung einzelner Spektralkomponenten dar und ist bei der Berechnung von nur einigen wenigen Spektralanteilen (engl. Bins) effizienter als alle blockbasierenden FFT-Algorithmen, welche immer das komplette diskrete Spektrum berechnen.
Anwendung
Die Kombination aus FFT und iFFT kann zur Kodierung und Dekodierung von Signalen auf Frequenzebene eingesetzt werden. Kompressionsalgorithmen wie der des MP3-Formats basieren hierauf (bzw. auf der verwandten diskreten Kosinustransformation). Ein weiteres wichtiges Anwendungsbeispiel ist die Breitbanddatenübertragung per OFDM, die Grundlage für ADSL und WLAN (Internet), DVB-T (Fernsehen), DRM und DAB (Radio) ist.
- Methode der Signalanalyse
- Schwingungsmesstechnik – Umrechnung Zeit in Frequenzendarstellung
- Akustik (Audiomessungen) – Berechnung von Spektrogrammen (Diagramme mit der Darstellung der Amplituden von den jeweiligen Frequenzanteilen)
- Längstwellenempfang mit dem PC
- Teil schneller, Polynome verarbeitender Algorithmen (z. B. Polynommultiplikation in O(nlogn)) in der Computeralgebra.
- Zur Reduzierung des Berechnungsaufwandes bei der zirkularen Faltung im Zeitbereich von FIR-Filtern und Ersatz durch die schnelle Fouriertransformation mit einfachen Multiplikationen im Frequenzbereich. (siehe auch Schnelle Faltung)
Literatur
- Zeitschriftenartikel
- James W. Cooley, John W. Tukey: An algorithm for the machine calculation of complex Fourier series. In: Math. Comput. 19, 1965, S. 297–301.
- C. M. Rader: Discrete Fourier transforms when the number of data samples is prime. In: Proc. IEEE 56, 1107–1108 (1968).
- Leo I. Bluestein: A linear filtering approach to the computation of the discrete Fourier transform. In: Northeast Electronics Research and Engineering Meeting Record 10, 1968, S. 218-219.
- Georg Bruun: z-Transform DFT filters and FFTs. In: IEEE Trans. on Acoustics, Speech and Signal Processing (ASSP) 26, Nr. 1, 1978, S. 56-63.
- M. T. Heideman, D. H. Johnson, C. S. Burrus : Gauss and the History of the Fast Fourier Transform. In: Arch. Hist. Sc. 34, Nr. 3, 1985.
- Bücher
- Alan V. Oppenheim, Ronald W. Schafer: Zeitdiskrete Signalverarbeitung. 3. Auflage. R. Oldenbourg Verlag, München/Wien 1999, ISBN 3-486-24145-1.
- E. Oran Brigham: FFT. Schnelle Fourier-Transformation. R. Oldenbourg Verlag, München/Wien 1995, ISBN 3-486-23177-4.
Weblinks
- www.inf.fh-flensburg.de/lang/algorithmen/fft/fft.htm – Beschreibung der Fourier-Transformation und Einheitswurzeln (Deutsch)
- www.fairaudio.de/lexikon-f.html#Fourier-Transformation – Bedeutung der FFT-Analyse in der Audiotechnik (Beispiel-Grafik: Rechtecksignal) (Deutsch)
- www.unet.univie.ac.at/~a0503736/php/floxwiki/pmwiki.php?n=Uni.FFT?action=downloadman&upname=fft.pdf – Bakkalaureatsarbeit, inklusive Fortran-Implementierung (pdf) (Deutsch)
- www.sprut.de/electronic/pic/16bit/dsp/fft/fft.htm – Einführung in die FFT für Nichtstudierte, z.B. Auszubildende (Deutsch)
- www.fftw.org (Englisch)
- www.nr.com – Buch Numerical Recipes, englisch, auch online verfügbar (Englisch)
- local.wasp.uwa.edu.au/~pbourke/other/dft/ (schöner FFT-Code in C, in 1D und 2D) (Englisch)
Wikimedia Foundation.