Satz von Fermat-Euler

Der Satz von Euler, auch als Satz von Euler-Fermat bekannt nach Leonhard Euler und Pierre de Fermat, stellt eine Verallgemeinerung des kleinen fermatschen Satzes auf nichtprime, beliebige Moduli 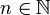$n\in\mathbb{N}$ dar. Er lautet: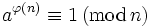

$a^{\varphi(n)} \equiv 1\,(\mathrm{mod}\,n)$

unter der Bedingung ggT(a,n) = 1, wobei φ(n) die Eulersche φ-Funktion bezeichnet, nämlich die Anzahl der zu n teilerfremden Reste modulo n. Da für prime Moduli p gilt φ(p) = p-1, geht für diese der Satz von Euler in den kleinen Satz von Fermat über.

Anwendungen

Der Satz von Euler dient der Reduktion großer Exponenten modulo n. Praktische Anwendung findet er in dieser Eigenschaft in der computergestützten Kryptographie, beispielsweise im RSA-Verschlüsselungsverfahren.

Beispiel

Was ist die letzte Ziffer im Dezimalsystem von 7²²², also welche Zahl ist 7²²² kongruent modulo 10?

Zunächst bemerken wir, dass ggT(7,10) = 1 und dass φ(10) = 4. Also liefert der Satz von Euler

$7^{\,4}\, \equiv 1\,(\mathrm{mod}\,10)$

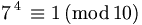
und wir erhalten

$7^{222} = 7^{\,4 \cdot 55 + 2} = (7^{\,4})^{55} \cdot 7^{2} \equiv 1^{55} \cdot 7^{2} = 49 \equiv 9\,(\mathrm{mod}\,10).$

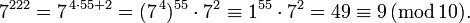
Allgemein gilt:

$a^b \equiv a^{b\,\mathrm{mod}\,\varphi(n)}\,(\mathrm{mod}\,n)\qquad a, b, n \in\mathbb{N} \wedge \mathrm{ggT}(a,n)=1$

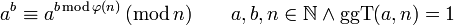
Beweis des Satzes von Euler

Sei 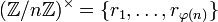$(\mathbb{Z}/n\mathbb{Z})^\times=\{r_1, \dots, r_{\varphi(n)}\}$ die Menge der multiplikativ modulo n invertierbaren Elemente. Für jedes a mit 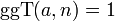$\operatorname{ggT}(a,n)=1$ ist dann 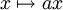$x\mapsto ax$ eine Permutation von 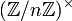$(\mathbb{Z}/n\mathbb{Z})^\times$, denn aus 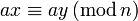$ax \equiv ay\,(\operatorname{mod}\,n)$ folgt $x\ \equiv y\,(\operatorname{mod}\,n)$.

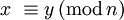Weil die Multiplikation kommutativ ist, folgt

$r_1\cdots r_{\varphi(n)} \equiv (ar_1)\cdots (ar_{\varphi(n)}) \equiv r_1\cdots r_{\varphi(n)}a^{\varphi(n)}\,(\operatorname{mod}\,n)$,

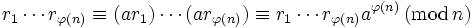und da die r_i invertierbar sind für alle i, gilt

$1 \equiv a^{\varphi(n)}\,(\operatorname{mod}\,n)$.

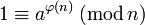Alternativbeweis

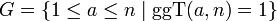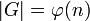Der Satz von Euler ist ein Sonderfall des folgenden Satzes aus den Elementen der Gruppentheorie: In jeder Gruppe G mit endlicher Ordnung m ist die m-te Potenz jedes Elements das Einselement. Hier ist $G=\{1\le a\le n\mid\operatorname{ggT}(a,n)=1\}$ also $|G|=\varphi(n)$, wobei die Operation von G die Multiplikation modulo n ist.

Siehe auch

• Kongruenz
• Teilbarkeit
• Zahlentheorie
• Kryptografie

Literatur

• Harald Scheid: Zahlentheorie, Spektrum Akademischer Verlag, 2003, ISBN 3-8274-1365-6