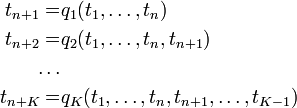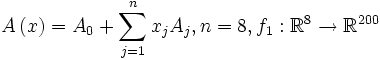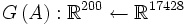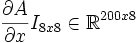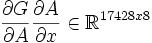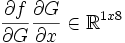- Automatische Differentiation
-
Das automatische Differenzieren bzw. Differenzieren von Algorithmen ist ein Verfahren der Informatik und angewandten Mathematik. Zu einer Funktion in mehreren Variablen, die als Prozedur in einer Programmiersprache oder als Berechnungsgraph gegeben ist, wird eine erweiterte Prozedur erzeugt, die sowohl die Funktion als auch einen oder beliebig viele Gradienten, bis hin zur vollen Jacobi-Matrix, auswertet. Wenn das Ausgangsprogramm Schleifen enthält darf die Anzahl der Schleifendurchläufe nicht von den unabhängigen Variablen abhängig sein.
Diese Ableitungen werden z. B. für das Lösen von nichtlinearen Gleichungssystemen mittels Newton-Verfahren und für Methoden der nichtlinearen Optimierung benötigt.
Das wichtigste Hilfsmittel dabei ist die Kettenregel sowie die Tatsache, dass zu den im Computer verfügbaren Elementarfunktionen wie sin, cos, exp, log die Ableitungen bekannt und genauso exakt berechenbar sind. Damit wird der Aufwand zur Berechnung der Ableitungen proportional (mit kleinem Faktor) zum Aufwand der Auswertung der Ausgangsfunktion.
Inhaltsverzeichnis
Berechnung von Ableitungen
Aufgabe: Gegeben eine Funktion
Wie erhält man Code/Funktion für Richtungsableitungen oder die volle Jacobi-Matrix
Verschiedene Ansätze hierfür sind:
- 1.) Versuche, eine geschlossene, analytische Form für f zu finden und bestimme
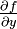 durch Differentiation „auf Papier“. Implementiere dann den Code für
durch Differentiation „auf Papier“. Implementiere dann den Code für 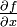 von Hand.
von Hand.
- Problem: Zu schwierig, zeitaufwendig, fehleranfällig
- 2.) Erzeuge die Berechnungsvorschrift für f in einem Computeralgebrasystem und wende die dort zur Verfügung stehenden Mittel zum symbolischen Differenzieren an. Exportiere dann den Code für
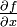 in seine eigentliche Umgebung.
in seine eigentliche Umgebung.
- Problem: Zeitaufwendig, skaliert nicht, zu kompliziert für größere Programme/Funktionen
- 3.) Bestimme eine numerische Approximation der Ableitung. Es gilt für kleines h
-
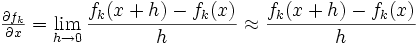 .
.
- Problem: wie findet man eine optimale Schrittweite h?
-
- 4) Stelle die Berechnungsvorschrift als Berechnungsbaum, d. h. als arithmetisches Netzwerk, dar und erweitere diesen unter Verwendung der Kettenregel zu einem Berechnungsbaum für Funktionswert und Ableitung
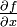 .
.
Die Idee der Automatischen Differentiation (AD)
Jedes Programm, das eine Funktion
 auswertet, kann als eine Abfolge von Zwischenschritten beschrieben werden, in welchen Zwischenergebnisse auf elementare Weise umgewandelt werden. Man kann sich dies so vorstellen, dass es eine (potentiell unendliche) Folge von Zwischenwerten
auswertet, kann als eine Abfolge von Zwischenschritten beschrieben werden, in welchen Zwischenergebnisse auf elementare Weise umgewandelt werden. Man kann sich dies so vorstellen, dass es eine (potentiell unendliche) Folge von Zwischenwerten 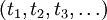 gibt und Funktionen
gibt und Funktionen 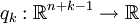 , die aber nur von ein oder zwei Variablen wirklich abhängen. Die Funktion wird ausgewertet, indem am Anfang
, die aber nur von ein oder zwei Variablen wirklich abhängen. Die Funktion wird ausgewertet, indem am Anfang 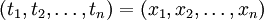 gesetzt wird und nacheinander
gesetzt wird und nacheinanderbestimmt wird. Dies kann so eingerichtet werden, dass die Funktionswerte von f sich in den zuletzt ausgewerteten Zwischenergebnissen befinden, d. h. am Ende wird noch
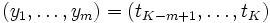 zugeordnet.
zugeordnet.AD beschreibt eine Menge von Verfahren, deren Ziel es ist ein neues Programm zu erzeugen, welches die Jacobimatrix von f,
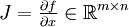 auswertet. Die Eingabevariablen x heißen unabhängige Variablen, die Ausgabevariable(n) y abhängige Variablen. Bei AD unterscheidet man mindestens zwei verschiedene Modi.
auswertet. Die Eingabevariablen x heißen unabhängige Variablen, die Ausgabevariable(n) y abhängige Variablen. Bei AD unterscheidet man mindestens zwei verschiedene Modi.- Vorwärtsmodus (FM engl. Forward Mode)
- Rückwärtsmodus (BM engl. Backward Mode)
Vorwärtsmodus
Im Vorwärtsmodus berechnet man das Matrixprodukt
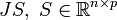
der Jacobi-Matrix mit einer beliebigen Matrix S (Seedmatrix), ohne vorher die Komponenten der Jacobi-Matrix zu bestimmen.
Beispiel
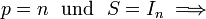 AD berechnet J
AD berechnet J
Im Vorwärtsmodus werden Richtungsableitungen entlang des Kontrollflusses der Berechnung von f transportiert. Für jede skalare Variable v wird in dem AD-erzeugten Code ein Vektor Dv erzeugt, dessen i-te Komponente die Richtungsableitung entlang der i-ten unabhängigen Variablen enthält.Beispiel
Berechne eine Funktion
![\begin{align}
& [ y_1 , y_2 , b ] = f\left(x_1, x_2, a\right) \left\{\right.\\
& \quad b=x_1+x_2 \\
& \quad y_1=a \cdot \sin(b) \\
& \quad y_2=b \cdot y_1 \\
& \left.\right\}
\end{align}](/pictures/dewiki/53/5b2cdbde0f0d9b6a212dd49f6b344364.png)
Eine Automatische Differentiation im Vorwärtsmodus hätte eine Funktion
![[y_1, y_2, Dy_1, Dy_2, b ] = f_{AD}\left( x_1, x_2, Dx_1, Dx_2, a\right)](/pictures/dewiki/97/ac738f56a966d94a582d98c50537cb97.png) zum Ergebnis:
zum Ergebnis:![\begin{align}
& [y_1, y_2, Dy_1, Dy_2, b ] = f_{AD}\left( x_1, x_2, Dx_1, Dx_2, a\right) \left\{\right. \\
& \quad b=x_1+x_2 \\
& \quad Db=Dx_1+ Dx_2 \\
& \quad y_1=a \cdot sin(b) \\
& \quad Dy_1=a\cdot cos(b) \cdot Db \\
& \quad y_2 = b \cdot y_1 \\
& \quad Dy_2 = Db \cdot y_1 + b \cdot Dy_1 \\
& \left.\right\}
\end{align}](/pictures/dewiki/51/3bd0c207191bef949f46561ea7b7d1f7.png)
Rückwärtsmodus
Der Rückwärtsmodus besteht aus zwei Phasen.
- Das Originalprogramm wird ausgeführt und gewisse Daten werden abgespeichert
- Das Originalprogramm wird rückwärts ausgeführt. Dabei werden Richtungsableitungen transportiert und es werden die Daten aus Phase 1 verwendet.
In Phase 2 wird für jede skalare Variable v ein Vektor av eingeführt. Dieser Vektor enthält in der i-ten Komponente die i-te Richtungsableitung (in Richtung von v). Die Saatmatrix befindet sich in ay. Im Rückwärtsmodus erhält man als Ergebnis ein Produkt
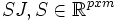
Beispiel 1
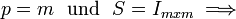 AD berechnet J
AD berechnet J
Beispiel 2
Für jede Rechenvorschriftszeile
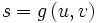 werden die Ableitungen von u und v auf folgendem Wege von s ergänzt:
werden die Ableitungen von u und v auf folgendem Wege von s ergänzt: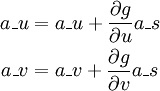
Gesucht sind die x1- und x2-Ableitungen von y2. Diese werden jeweils als a_x1 und a_x2 bezeichnet. Der Wert a_y2 wird mit 1 initialisiert, alle anderen a_...-Werte werden mit 0 initialisiert.
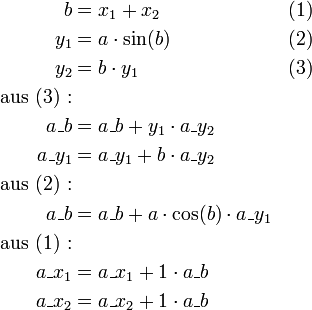
Effizienzbetrachtungen
Die Effizienz von AD-Algorithmen hängt vom Modus und dem Parameter p ab. Die Wahl des Modus und des Parameters p hängt davon ab, wofür die Jacobimatrix berechnet wird. Es gelte
Tf die Zeit f zu berechnen Mf der Speicherbedarf dieser Rechnung TJS die Zeit f und JS zu berechnen MJS der Speicherbedarf dieser Rechnung TSJ die Zeit f und SJ zu berechnen MSJ der Speicherbedarf dieser Rechnung Für die beiden vorgestellten Modi gilt
- Vorwärtsmodus:
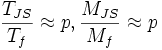
- Rückwärtsmodus:
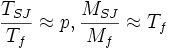
Die Berechnung als Kette von Berechnungen
Gegeben:
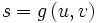 , Frage: Wie verändert sich die Ableitung von s während der 2ten Phase, um die Ableitungen von u und v zu erhalten?
, Frage: Wie verändert sich die Ableitung von s während der 2ten Phase, um die Ableitungen von u und v zu erhalten?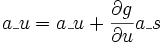
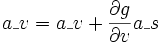
f(x) wird als Sequenz von Programmen interpretiert. Im Beispiel „Optimierung eines Tragflügels“ umfasst die Berechnung die folgenden Schritte.
- Überlagerung des Tragflügels mit sogenannten „Mode-Funktionen“
- Berechnung eines Gitters, das um den Tragflügel herum gelegt wird
- Lösung der Navier-Stokes-Gleichungen auf dem Gitter und Berechnung der Integrals der selbigen.
-
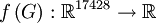
Insgesamt ergibt sich die Funktion
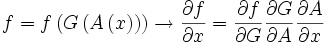
Mit einem naivem Ansatz würde man drei Matrizen
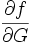 ,
,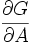 ,
,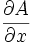 berechnen und dann zwei Matrix-Matrix Multiplikationen durchführen. Der Nachteil des Vorwärtsmodus ist allerdings:
berechnen und dann zwei Matrix-Matrix Multiplikationen durchführen. Der Nachteil des Vorwärtsmodus ist allerdings: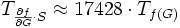
im Rückwärtsmodus würde analog
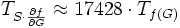
gelten. Ein besserer Ansatz ist, das Ergebnis einer Berechnung jeweils als Saatmatrix der folgenden einzusetzen.
- Wähle
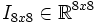 als Saatmatrix der ersten Rechnung
als Saatmatrix der ersten Rechnung - Das Ergebnis der ersten Rechnung als Saatmatrix der zweiten Rechnung
- Das Ergebnis der zweiten Rechnung als Saatmatrix der dritten Rechnung
also
Da die Zeilenzahl jeder Matrix 8 (p=8) ist erhöht sich der Zeit- und Speicherbedarf ebenfalls um höchstens 8.
Literatur
- Andreas Griewank, Andrea Walther (2008): Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition, SIAM, xxii + 438 Seiten, ISBN 978-0-898716-59-7
- George F. Corliss ; Andreas Griewank (1993): "Operator Overloading as an Enabling Technology for Automatic Differentiation", Technical Report MCS-P358-0493, Mathematics and Computer Science Division, Argonne National Laboratory
Weblinks
-
Wikimedia Foundation.

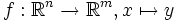
![\frac{\partial f}{\partial x}=\left[ \tfrac{\partial y_i}{\partial x_j} \right]_{i=1..m, j=1..n} \ ?](/pictures/dewiki/100/d3a5055aef43666da1fff7fcbff51479.png)