Rationale Funktion

rot: Graph der gebrochenrationalen Funktion f mit $f(x)=\tfrac{2(x + 2)(x + 1)(x - 1)^2}{(x + 1)(2x - 1)}$
blau: Polgerade durch die Polstelle bei x = 0.5
grün: Asymptotenfunktion g mit g(x) = x² + x / 2 − 11 / 4, stetig behebbare Definitionslücke bei x = − 1

Eine rationale Funktion ist in der Mathematik eine Funktion, deren Term sich in der Form

$f(x)=\frac{a_z x^z+a_{z-1} x^{z-1}+\cdots +a_1x+a_0}{b_n x^n+b_{n-1} x^{n-1}+\cdots +b_1x+b_0} = \frac{P_z(x)}{Q_n(x)}$

mit natürlichen Zahlen n und z schreiben lässt, also als Quotient zweier Polynome darstellbar ist. Die Funktion ist also ein Quotient zweier ganzrationaler Funktionen. Die Zahlen a_z, ..., a₀, b_n, ... b₀ können beliebige reelle Zahlen (oder auch komplexe Zahlen) sein; die einzige Einschränkung ist, dass $b_n \ne 0$ sein muss. Die rationalen Funktionen gehören zu den meromorphen Funktionen.

Einteilung

• Ist das Nennerpolynom Q_n vom Grad n = 0, also konstant, so spricht man von einer ganzrationalen Funktion oder von einer Polynomfunktion.
• Kann man den Funktionsterm nur mit einem Nennerpolynom vom Grad n > 0 darstellen, so handelt es sich um eine gebrochenrationale Funktion.
  • Ist n > 0 und z < n, so handelt es sich um eine echt gebrochenrationale Funktion.
  • Ist n > 0 und z ≥ n, so handelt es sich um eine unecht gebrochenrationale Funktion. Sie kann über Polynomdivision in eine ganzrationale Funktion und eine echt gebrochenrationale Funktion aufgeteilt werden (siehe unten).

Beispiele:

• Die rationale Funktion $f: x \mapsto \frac{3x^3 - 4x + 5}{2}$ kann auch geschrieben werden als $f: x \mapsto \frac{3}{2} x^3 - 2x + \frac{5}{2}$, ist also eine ganzrationale Funktion.
• Die rationale Funktion $f: x \mapsto \frac{2x - 1}{x^2 + 1}$ hat den Zählergrad z = 1 und den Nennergrad n = 2, ist also eine echt gebrochenrationale Funktion.
• Die rationale Funktion $f: x \mapsto \frac{(x - 1)^2 \cdot (x + 2)}{x \dot (2 - 3x^2)}$ kann auch geschrieben werden als $f: x \mapsto \frac{x^3 - 3x + 2}{2x - 3x^3}$, hat also den Zählergrad z = 3 und auch den Nennergrad n = 3; damit ist sie eine unecht gebrochenrationale Funktion.
• Die rationale Funktion $f: x \mapsto x + 1 + \frac{1}{x-1}$ kann auch geschrieben werden als $f: x \mapsto \frac{x^2}{x-1}$; da der Zählergrad z = 2 und der Nennergrad n = 1 ist, handelt es sich auch dabei um eine unecht gebrochenrationale Funktion.

Asymptotisches Verhalten

Für das Verhalten für x gegen Unendlich sind die Grade z bzw. n des Zähler- bzw. Nenner-Polynoms entscheidend:

Für $x\to\infty$ geht f(x)

• gegen $\sgn\left(\tfrac{a_z}{b_n}\right)\cdot\infty$, falls z > n, wobei mit „sgn“ das Vorzeichen des Quotienten gemeint ist (siehe Signum),
• gegen $\tfrac{a_z}{b_n}$, falls z = n (die Asymptote ist parallel zur x-Achse),
• gegen 0 (die x-Achse ist waagrechte Asymptote), falls z < n,

Für $x\to -\infty$ ergibt sich im zweiten und dritten Fall jeweils derselbe Grenzwert wie für $x \to \infty$. Im ersten Fall muss man Zähler- und Nennergrad noch genauer berücksichtigen:

• Ist z − n gerade, so ergibt sich derselbe Grenzwert wie für $x \to \infty$.
• Ist z − n ungerade, so ändert sich im Vergleich zu $x \to \infty$ das Vorzeichen des Grenzwerts.

Wie weiter unten beschrieben, kann man im ersten Fall den Funktionsterm mittels Polynomdivision immer in ein Polynom und einen echt gebrochenrationalen Term zerlegen; das Polynom beschreibt dann eine sogenannte Asymptotenkurve. (Das Verhalten der Funktionswerte für $x \to \pm \infty$ kann man dann auch einfacher erhalten, indem man nur das Verhalten der Asymptotenkurve untersucht.) Im Sonderfall z = n + 1 ergibt sich eine schräg verlaufende Asymptote.

Beispiele:

• Bei der gebrochenrationalen Funktion $f: x \mapsto \frac{2x - 1}{x^2 + 1}$ ist der Zählergrad z = 1 und der Nennergrad n = 2, der Grenzwert für $x \to \pm \infty$ ist also 0.
• Die gebrochenrationale Funktion $f: x \mapsto \frac{x^3 - 3x + 2}{2x - 3x^3}$ hat den Zählergrad z = 3 und auch den Nennergrad n = 3; da hier a₃ = 1 und b₃ = − 3 ist, ergibt sich für die Gleichung der waagrechten Asymptote: $y = -\frac{1}{3}$.
• Die gebrochenrationale Funktion $f: x \mapsto \frac{x^2}{x-1}$ hat den Zählergrad z = 2 und den Nennergrad n = 1; mit den Koeffizienten a₂ = 1 und b₁ = 1 ergibt sich also: $f(x) \to \sgn\left(\tfrac{1}{1}\right)\cdot\infty = +\infty$ für $x \to \infty$. Da hier z − n = 1 ungerade ist, folgt für den Grenzwert für $x \to -\infty$ das umgedrehte Vorzeichen, also $f(x) \to -\infty$. Diese Funktion kann man auch schreiben als $f: x \mapsto x + 1 + \frac{1}{x-1}$, das heißt, die (schräge) Asymptote hat die Gleichung y = x + 1 (und daraus ergibt sich auch leicht wieder das eben geschilderte Grenzverhalten).

Kurvendiskussion

Anhand des Funktionsterms der rationalen Funktion $f={p\over q}:x\mapsto \frac{p(x)}{q(x)}$ lassen sich folgende Aussagen zum Funktionsgraphen machen.

Symmetrie

Eine Polynomfunktion (ganzrationale Funktion) ist gerade/ungerade, wenn alle Exponenten gerade/ungerade sind. Sind Zählerpolynom p und Nennerpolynom q von einem dieser beiden Typen, so ist auch die rationale Funktion f gerade oder ungerade:

• Sind p und q beide gerade oder beide ungerade, so ist f gerade (d.h. der Graph ist symmetrisch zur y-Achse)
• Ist p gerade und q ungerade, so ist f ungerade (d.h. der Graph ist punktsymmetrisch zum Ursprung); gleiches gilt, wenn p ungerade und q gerade ist.

In allen anderen Fällen, wenn also Zähler- oder Nennerfunktion oder beide weder gerade noch ungerade sind, sind Symmetrieeigenschaften von f schwieriger zu entscheiden. (Siehe auch Kurvendiskussion und Symmetrie in der Geometrie).

Beispiele:

• Der Graph zur Funktion f mit $f(x) = \frac{2x^3 - 3x}{x^2+1}$ ist symmetrisch zum Ursprung, da p ungerade und q gerade, die Funktion insgesamt also ungerade ist.

• Der Graph zur Funktion $f: x \mapsto \frac{x^5-x^3}{x^3+x}$ ist symmetrisch zur y-Achse, da p und q beide ungerade, die Funktion insgesamt also gerade ist. Dies kann man auch anders sehen: Klammert man in Zähler und Nenner jeweils x aus, kann man den Funktionsterm kürzen zu $f(x) = \frac{x^4-x^2}{x^2+1}$; nun sind p und q gerade, die Funktion insgesamt also wiederum gerade.

• Beim Graph zur Funktion mit dem Term $f(x) = \frac{x}{x-1}$ ist zunächst keine Symmetrie erkennbar (p ist ungerade, q aber weder gerade noch ungerade); man kann aber zeigen, dass der Graph symmetrisch zum Punkt P(1|1) ist; es gilt nämlich:

  $f(1+x) - 1 = \frac{1+x}{(1+x)-1} - 1 = \frac{1+x}{x} - \frac{x}{x} = \frac{1}{x}$ und

  $1 - f(1-x) = 1 - \frac{1-x}{(1-x)-1} = \frac{x}{x} + \frac{1-x}{x} = \frac{1}{x}$,

also insgesamt: f(1 + x) − 1 = 1 − f(1 − x), was eben gerade Symmetrie zum Punkt P(1|1) bedeutet. Alternativ kann man auch zeigen, dass der Graph von f aus dem Graph der Funktion $g: x \mapsto \frac{1}{x}$ (welcher symmetrisch zum Ursprung ist) durch Verschieben um 1 in x-Richtung und um 1 in y-Richtung hervorgeht.

Definitionsbereich, Nullstellen und Polstellen

Die gebrochenrationale Funktion ist an den Nullstellen der Nennerfunktion q nicht definiert.

Die Nullstellen einer gebrochenrationalen Funktion werden durch diejenigen Nullstellen der Zählerfunktion p bestimmt, die zum Definitionsbereich der gesamten Funktion gehören.

Ein Spezialfall ergibt sich, wenn eine reelle Zahl $a\in\R$ gleichzeitig Nullstelle des Zählerpolynoms und des Nennerpolynoms ist. Dann sind Zähler- und Nennerpolynom durch den zugehörigen Linearfaktor x − a (eventuell sogar mehrfach) teilbar, das heißt der Funktionsterm kann mit diesem Faktor (eventuell mehrfach) gekürzt werden.

• Kommt x − a im Nenner öfter vor als im Zähler, so liegt eine Polstelle vor (die entsprechende Potenz heißt dann die Vielfachheit der Polstelle);
• andernfalls hat die rationale Funktion an der Stelle a eine stetig behebbare Definitionslücke, und man kann die Funktion stetig fortsetzen

Beispiele:

• Die Funktion $f: x \mapsto \frac{x-1}{(2x-4)^2}$ hat den Definitionsbereich $\mathbb{D} = \mathbb{R}\setminus\{2\}$, da die Nennerfunktion $q: x \mapsto (2x-4)^2$ die Nullstelle x = 2 hat, und die Nullstelle x = 1, da dies die einzige Nullstelle der Zählerfunktion $p: x \mapsto x-1$ ist (und x = 1 zu $\mathbb{D}$ gehört). x = 2 ist eine (doppelte) Polstelle.

• Die Funktion $f: x \mapsto \frac{x^2-x}{x^2-1}$ hat den Definitionsbereich $\mathbb{D}_f = \mathbb{R}\setminus\{\pm 1\}$. Hier ist aber nun x = 1 eine Nullstelle der Zähler- und der Nennerfunktion. Um den entsprechenden Linearfaktor (x − 1) zu kürzen, faktorisiert man Zähler und Nenner zunächst (durch Ausklammern bzw. Anwenden der binomischen Formeln); dies führt auf $f: x \mapsto \frac{x \cdot(x-1)}{(x+1)\cdot (x-1)}$ bzw. nach kürzen auf $f: x \mapsto \frac{x}{x+1}$. Damit ergibt sich: x = − 1 ist eine (einfache) Polstelle, x = 1 dagegen eine stetig behebbare Definitionslücke von f, und f hat die Nullstelle x = 0 (beachte: x = 1 ist keine Nullstelle von f, da dieser Wert nicht zu $\mathbb{D}$ gehört!). Für die stetige Fortsetzung von f ergibt sich: $\tilde{f}(x) = \frac{x}{x+1}$ und $\mathbb{D}_{\tilde{f}} = \mathbb{R}\setminus\{-1\}$.

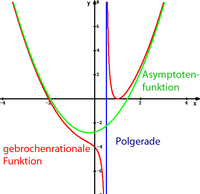
Asymptote

Durch die Polynomdivision von p durch q erhält man $p = g\cdot q + r$ mit Polynomen g und r, wobei der Grad von r kleiner als der von q ist. Das asymptotische Verhalten von

$f = {p\over q} = g + {r\over q}$

ist damit durch die ganzrationale Funktion ("Asymptotenfunktion") g bestimmt (die konkrete Durchführung der Polynomdivision ist nur bei 3. und 4. notwendig):

1. z < n → x-Achse ist Asymptote: g(x) = 0
2. z = n → waagerechte Asymptote: $g(x) = \frac{a_z}{b_n}$
3. z = n + 1 → schräge Asymptote: $g(x) = mx + c \,; m \ne 0$ (Spezialfall von 4)
4. z > n + 1 → ganzrationale Näherungsfunktion

Ableitung

Zum Ableiten gebrochenrationaler Funktionen muss man im Allgemeinen die Quotientenregel verwenden; zusätzlich kann auch oft die Kettenregel nützlich sein, beispielsweise wenn die Nennerfunktion eine Potenz eines Binoms ist. Vor dem Ableiten empfiehlt es sich oft, den Funktionsterm zunächst mit Hilfe einer Polynomdivision umzuschreiben und den übrigen echt gebrochenrationalen Term zu kürzen.

Beispiele:

• Bei der Funktion $f: x \mapsto \frac{2x-1}{(x^2+1)^2}$ ist es sinnvoll, neben der Quotientenregel auch die Kettenregel anzuwenden, statt zunächst im Nenner die erste binomische Formel anzuwenden. Mit der Kettenregel ergibt sich zunächst für die Ableitung der Nennerfunktion q (in der Quotientenregel meist mit v bezeichnet):

  $q'(x) = 2 (x^2+1) \cdot 2x = 4x (x^2+1)$,

und damit insgesamt für die Ableitungsfunktion von f:

$f'(x) = \frac{2 \cdot (x^2+1)^2 - (2x - 1) \cdot 4x (x^2+1)}{(x^2+1)^4}$.

Nun kann man im Zähler einen Faktor (x² + 1) ausklammern und kürzen:

$f'(x) = \frac{2 \cdot (x^2+1) - (2x - 1) \cdot 4x}{(x^2+1)^3}$.

Vereinfachen des Zählers führt schließlich auf

$f'(x) = \frac{-6 x^2 + 4x + 2}{(x^2+1)^3}$.

• Den Funktionsterm $f(x) = \frac{x^4+x^3-7x^2-12x-4}{3x^3+12x^2+12x}$ bringt man mit Hilfe einer Polynomdivision zunächst auf die Form

  $f(x) = \frac{1}{3} x - 1 + \frac{x^2-4}{3x^3+12x^2+12x}$,

woran man auch gleich die Gleichung der schrägen Asymptote ablesen kann:

$y = \frac{1}{3}x - 1$.

Faktorisieren von Zähler und Nenner führt dann auf

$f(x) = \frac{1}{3} x - 1 + \frac{(x + 2) (x - 2)}{3x (x + 2)^2}$,

man kann also einen Faktor (x + 2) kürzen. Schließlich hat man:

$f(x) = \frac{1}{3} x - 1 + \frac{x - 2}{3x^2 + 6x}$;

in dieser Form kann man die Funktion nun deutlich leichter ableiten als in der ursprünglich gegebenen.

Mit Hilfe der Quotientenregel ergibt sich:

$f'(x) = \frac{1}{3} + \frac{1 \cdot (3x^2+6x) - (x - 2) \cdot (6x + 6)}{(3x^2+6x)^2} = \frac{1}{3} + \frac{-3x^2 + 12 x + 12}{(3x^2+6x)^2} = \frac{1}{3} + \frac{-x^2+4x+4}{3 x^2 (x+2)^2}$.

Setzt man die erste Ableitung gleich Null, um die Extremstellen zu suchen, so empfiehlt es sich vorher, die beiden Brüche wieder zusammen zu fassen:

$f'(x) = \frac{x^2 (x+2)^2 - x^2+4x+4}{3 x^2(x+2)^2} = \frac{x^4 + 4x^3 + 3 x^2 + 4x + 4}{3 x^2 (x+2)^2}$.

Stammfunktion

Im Gegensatz zu den ganzrationalen Funktionen ist es bei gebrochenrationalen Funktionen oft relativ schwierig, eine Stammfunktion zu finden. Hierzu kann man, je nach Form der gebrochenrationalen Funktion, unter anderem folgende Regeln anwenden (meist muss man den Funktionsterm durch Umformungen und/oder Substitution zunächst in eine passende Form bringen):

$\int \frac{1}{mx + a} dx = \frac{1}{m} \cdot \ln(mx + a) + C$ für $m, a \in \mathbb{R}, m \ne 0$

$\int \frac{1}{(mx + a)^n} dx = \frac{1}{m} \cdot \frac{-1}{n-1} \cdot \frac{1}{(mx + a)^{n-1}} + C$ für $m, a \in \mathbb{R}, m \ne 0, n \in \mathbb{N}\setminus\{0; 1\}$

$\int \frac{1}{x^2+1} dx = \operatorname{arctan} (x) + C$ oder = − arccot(x) + C

$\int \frac{1}{x^2-1} dx = \operatorname{artanh} (x) + C = \frac{1}{2} \ln\left(\frac{1+x}{1-x}\right)$ für | x | < 1

$\int \frac{1}{x^2-1} dx = \operatorname{arcoth} (x) + C = \frac{1}{2} \ln\left(\frac{x+1}{x-1}\right)$ für | x | > 1

$\int \frac{u'(x)}{u(x)} dx = \ln |u(x)| + C$ für $u(x) \ne 0$

Oft kann für die Bestimmung einer Stammfunktion auch die Partialbruchzerlegung hilfreich sein.

Beispiele:

• Gesucht sei eine Stammfunktion zu $f(x) = \frac{5x - 1}{3x + 2}$. Mittels einer Polynomdivision kann man dies zunächst umschreiben zu:

  $f(x) = \frac{5}{3} - \frac{13}{9x+6}$.

Anwenden der ersten Regel liefert dann als mögliche Stammfunktion:

$F(x) = \frac{5}{3} x - \frac{13}{9} \ln(9x+6)$.

• Gesucht sei eine Stammfunktion zu $f(x) = \frac{x^2 + 1}{x^2-1}$, wobei x zwischen -0,5 und 0,5 liegen soll. Wieder kann man den Funktionsterm zunächst mittels einer Polynomdivision umschreiben:

  $f(x) = 1 + \frac{2}{x^2-1}$.

Anwenden der vierten Regel liefert dann als mögliche Stammfunktion:

$F(x) = x + 2 \cdot \operatorname{artanh} (x)$.

• Gesucht sei eine Stammfunktion zu $f(x) = \frac{x+2}{x^2+4x+5}$. Dies kann auch geschrieben werden als

  $f(x) = \frac{1}{2} \frac{2x+4}{x^2+4x+5} = \frac{1}{2} \frac{u'(x)}{u(x)}$ mit u(x) = x² + 4x + 5.

Anwenden der letzten Regel liefert dann als mögliche Stammfunktion:

$F(x) = \frac{1}{2} \ln(x^2+4x+5)$.

• Eine Stammfunktion zu $f(x) = \frac{1}{x^2+2x+2}$ kann man mit Hilfe der Substitution y = x + 1 bestimmen, nachdem man den Nenner mittels quadratischer Ergänzung umgeformt hat:

  $\begin{align}\int \frac{1}{x^2+2x+2} dx &= \int \frac{1}{(x+1)^2+1} dx = \int \frac{1}{y^2+1} dy\\ &= \operatorname{arctan}(y) + C = \operatorname{arctan}(x+1) + C \end{align}$

• Eine Stammfunktion zu $f(x) = \frac{1}{x^2-x-6}$ kann man mit Hilfe der Partialbruchzerlegung erhalten, nachdem man den Nenner zunächst faktorisiert hat:

  $\begin{align} \int \frac{1}{x^2-x-6} dx &= \int \frac{1}{(x-3)(x+2)} dx = \int \frac{1}{5} \left(\frac{1}{x-3} - \frac{1}{x+2} \right) dx\\ &= \frac{1}{5} \left(\ln(x-3) - \ln(x+2)\right) + C = \frac{1}{5} \ln\left(\frac{x-3}{x+2}\right) + C\end{align}$

Anwendungen

Rationale Funktionen haben vielfältige Anwendungen in Naturwissenschaften und Technik:

• Viele Größen sind umgekehrt proportional zueinander, eine der Größen ist also eine rationale Funktion der anderen, wobei der Zähler konstant und der Nenner eine (homogene) lineare Funktion ist. Einige wenige Beispiele:
  • Die Geschwindigkeit v und die für eine feste Strecke s benötigte Zeit t sind umgekehrt proportional zueinander: $t(v) = \frac{s}{v}$
  • Die Konzentration c eines Stoffes ist bei fester Stoffmenge n umgekehrt proportional zum Volumen V des Lösungsmittels: $C(V) = \frac{n}{V}$
  • Beschleunigung und Masse sind bei fester Kraft F umgekehrt proportional zueinander: $a(m) = \frac{F}{m}$.
  • Für die Kapazität C eines Plattenkondensators gilt in Abhängigkeit vom Plattenabstand d: $C(d) = \epsilon_0 \epsilon_r \frac{A}{d}$ mit dem Flächeninhalt A der Platten, der elektrischen Feldkonstante $\epsilon_0$ und der Permittivität $\epsilon_r$.
• In vielen Bereichen der Physik kommen Funktionen von zwei Variablen x und y der folgenden Form vor: $f(x;y) = \frac{xy}{x \pm y}$. Ist eine der beiden Variablen, z. B. y, konstant oder wählt man sie als Parameter, so ergibt sich eine rationale Funktion (bzw. Funktionenschar) von x. Solche Funktionen treten immer dann auf, wenn sich der gesamte Kehrwert irgendeiner Größe als Summe oder Differenz der Kehrwerte zweier anderer Funktionen ergibt.
  • Mittels der Linsengleichung der Optik kann man die Brennweite f als Funktion von Gegenstandsweite g und Bildweite b darstellen: $f(g;b)= \frac{gb}{g+b}$; umstellen nach g oder b liefern eine sehr ähnliche Funktion, allerdings mit - statt mit +.
  • Für den Gesamtwiderstand R einer Parallelschaltung zweier Widerstände R₁ und R₂ ergibt sich: $R = \frac{R_1 R_2}{R_1 + R_2}$; eine analoge Formel gilt bei der Reihenschaltung zweier Kondensatoren.
  • In der Mechanik ergibt sich, wenn man zwei Federn mit Federkonstanten D₁ und D₂ aneinander hängt, für die gesamte Federkonstante D der Anordnung: $D = \frac{D_1 D_2}{D_1 + D_2}$
• Bei einem Spannungsteiler ist die gesamte an einem Widerstand R abfallende Spannung U gegeben durch: $U(R) = \frac{U_0 R}{R + R'}$, wobei U₀ die zu teilende Spannung und R' der andere Widerstand ist.
• Für die elektrische Leistung P, die ein Gerät mit Widerstand R erbringt, das an einer Spannungsquelle (Spannung U) mit Innenwiderstand R_i angeschlossen ist, ergibt sich: $P(R) = \frac{U^2 R}{(R + R_i)^2}$. Die größtmögliche Leistung (zu bestimmen mit Hilfe der Differenzialrechnung) erhält man also dann, wenn R = R_i ist (Leistungsanpassung).
• Für die Induktivität L einer (nicht zu kurzen) Spule in Abhängigkeit von ihrem Radius r gilt: $L(r) = \frac{\mu_0 N^2 \pi r^2}{l + r/1,1}$. Dabei ist l die Länge der Spule (man kann L also auch als rationale Funktion von l auffassen), N die Windungszahl und μ₀ die magnetische Feldkonstante.
• Die Bremskraft B einer Wirbelstrombremse hängt folgendermaßen von der Geschwindigkeit v ab: $B(v) = \frac{av}{b + v^2}$ mit Konstanten a und b.
• Bei der Atwoodschen Maschine hängt die Beschleunigung a folgendermaßen von den beiden Massen m und M ab: $a = \frac{m}{2M+m} \cdot g$; man kann a also als rationale Funktion sowohl von m als auch von M auffassen.
• Auch geometrische Fragestellungen führen oft auf rationale Funktionen. Beispiel: Bei einer Truhe, die aus einem Quader (Grundseitenlängen l und 2r, Höhe r) mit aufgesetztem Halb-Zylinder (Höhe l, Radius r) besteht, gilt für den Oberflächeninhalt O in Abhängigkeit von r bei gegebenem Volumen V: $O(r) = \frac{(\pi + 4)r^3 + 2V}{r}$

Abweichende Bedeutung in der Höheren Algebra

In der Abstrakten Algebra wird der Begriff einer rationalen Funktion in einem allgemeineren und etwas unterschiedlichen Sinne verwendet. Und zwar versteht man unter einer rationalen Funktion in n Variablen $X_1,\ X_2,\ ...,\ X_n$ über einem Körper K ein Element des Quotientenkörpers des Polynomrings $K\left[X_1,X_2,...,X_n\right]$. Dieser Quotientenkörper wird Rationaler Funktionenkörper genannt. Im Allgemeinen ist eine rationale Funktion also keine Funktion irgendeiner Art, sondern ein (formaler) Bruch aus zwei Polynomen. Der Unterschied macht sich allerdings nur über endlichen Körpern bemerkbar: So ist z. B. für jede Primzahl p über dem endlichen Körper $\mathbb F_p$ (dem Körper aller Restklassen ganzer Zahlen modulo p) der Bruch $\tfrac{1}{X^p-X}$ eine wohldefinierte rationale Funktion in der Variablen X, aber keine Funktion im eigentlichen Sinne des Begriffes, weil man in diese Funktion keinen einzigen Wert einsetzen darf, ohne dass der Nenner 0 wird. (Denn setzt man irgendein $x\in\mathbb F_p$ in diese „Funktion“ ein, erhält man $\tfrac{1}{x^p-x}$, was undefiniert ist, weil der Nenner x^p − x nach dem kleinen Fermatschen Satz gleich 0 ist.) Über unendlichen Körpern allerdings ist eine rationale Funktion immer eine Funktion, die zwar Definitionslücken haben kann, aber diese Definitionslücken sind nur „sehr wenige“ im Vergleich zu den Werten, die man in die Funktion einsetzen darf. Dieser Gedanke wird mit dem Begriff der Zariski-Topologie formalisiert (die Definitionslücken bilden eine Zariski-offene Menge, und das Komplement dieser Menge, also die einsetzbaren Werte, bilden eine Zariski-dichte Menge).

Weblinks

 Commons: Rationale Funktionen – Sammlung von Bildern, Videos und Audiodateien

Rationale Funktionen - Ein Digitales Lehrbuch © 2000 - 2001 by Henning Koch