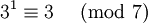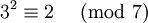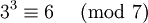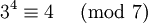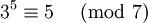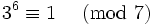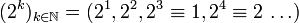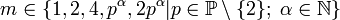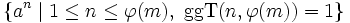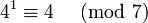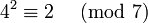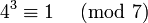- Primitive Wurzel
-
Als Primitivwurzeln werden in der Zahlentheorie, einem Teilgebiet der Mathematik bestimmte Elemente von primen Restklassengruppen bezeichnet. Die besondere Eigenschaft einer Primitivwurzel ist, dass jedes Element der primen Restklassengruppe als Potenz der Primitivwurzel dargestellt werden kann.
Inhaltsverzeichnis
Beispiel
Die Zahl 3 ist eine Primitivwurzel modulo 7, da gilt
Es lassen sich also alle Elemente
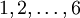 der primen Restklassengruppe modulo 7 als Potenzen von 3 darstellen. Die Zahl 2 ist keine Primitivwurzel modulo 7, da
der primen Restklassengruppe modulo 7 als Potenzen von 3 darstellen. Die Zahl 2 ist keine Primitivwurzel modulo 7, da 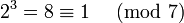 ist, daher wiederholen sich die Reste in der Folge der Potenzen von 2 modulo 7
ist, daher wiederholen sich die Reste in der Folge der Potenzen von 2 modulo 7bereits nach jeweils 3 Schritten, daher werden nicht alle 6 verschiedenen primen Reste modulo 7 erreicht und 2 erzeugt die prime Restklassengruppe nicht.
Definition und Existenzbedingungen
Eine ganze Zahl a ist eine Primitivwurzel modulo m, wenn die Restklasse
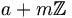 die prime Restklassengruppe
die prime Restklassengruppe 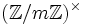 erzeugt. Dies ist gleichbedeutend damit, dass eine ganze Zahl a genau dann eine Primitivwurzel modulo m ist, wenn die Ordnung von a modulo m gleich der Gruppenordnung der primen Restklassengruppe ist:
erzeugt. Dies ist gleichbedeutend damit, dass eine ganze Zahl a genau dann eine Primitivwurzel modulo m ist, wenn die Ordnung von a modulo m gleich der Gruppenordnung der primen Restklassengruppe ist: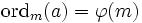 .
.
Hierbei ist
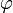 die Eulersche φ-Funktion und
die Eulersche φ-Funktion und 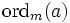 die multiplikative Ordnung modulo m des Elements a, d. h. der kleinste positive Exponent n, für welchen
die multiplikative Ordnung modulo m des Elements a, d. h. der kleinste positive Exponent n, für welchen 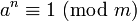 ist (für die Schreibweise „mod“ siehe Modulo).
ist (für die Schreibweise „mod“ siehe Modulo).Es gibt genau dann Primitivwurzeln modulo m, wenn die prime Restklassengruppe
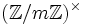 eine zyklische Gruppe ist. Dies ist nach einem Satz von C. F. Gauß genau dann der Fall, wenn für den Modul
eine zyklische Gruppe ist. Dies ist nach einem Satz von C. F. Gauß genau dann der Fall, wenn für den Modulgilt. Dabei bezeichnet
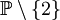 die Menge der ungeraden Primzahlen.[1]
die Menge der ungeraden Primzahlen.[1]
Wenn modulo m Primitivwurzeln existieren, dann existieren genau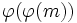 modulo m inkongruente Primitivwurzeln. Jede dieser Primitivwurzeln ist modulo m kongruent zu einem Element der Menge:
modulo m inkongruente Primitivwurzeln. Jede dieser Primitivwurzeln ist modulo m kongruent zu einem Element der Menge:wobei a eine beliebige Primitivwurzel modulo m ist.
Berechnung von Primitivwurzeln
Um festzustellen, ob eine Zahl a Primitivwurzel modulo m ist, wird zuerst
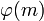 und anschließend die Ordnung von a berechnet. Die Ordnung lässt sich beispielsweise bestimmen, indem nacheinander die Werte atmod m für
und anschließend die Ordnung von a berechnet. Die Ordnung lässt sich beispielsweise bestimmen, indem nacheinander die Werte atmod m für 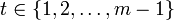 berechnet werden. Das erste t, für das atmod m = 1 gilt, ist die Ordnung von a.
berechnet werden. Das erste t, für das atmod m = 1 gilt, ist die Ordnung von a.Beim Beispiel aus der Einleitung sieht man, dass die 3 die Ordnung 6 hat. Da zudem
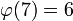 gilt, ist 3 eine Primitivwurzel modulo 7.
gilt, ist 3 eine Primitivwurzel modulo 7.Eine Zahl, die keine Primitivwurzel modulo 7 ist, ist die 4. Hier gilt
Die Ordnung von 4 ist deshalb 3 und die 4 keine Primitivwurzel modulo 7.
Primitivwurzeln modulo Primzahlen
Die primen Restklassengruppen zu Modulen m, die Primzahlen sind, bestehen aus genau m − 1 Elementen. Die Zahlen
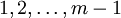 sind die Repräsentanten der unterschiedlichen Restklassen. Ist a eine Primitivwurzel modulo m, so nimmt der Ausdruck atmod m für
sind die Repräsentanten der unterschiedlichen Restklassen. Ist a eine Primitivwurzel modulo m, so nimmt der Ausdruck atmod m für 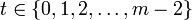 alle Werte aus
alle Werte aus 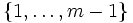 (in scheinbar zufälliger Reihenfolge) an.
(in scheinbar zufälliger Reihenfolge) an.Die folgende Tabelle zeigt die Primitivwurzeln modulo der Primzahlen bis 29.
m 
Primitivwurzeln modulo m 2 1 1 3 1 2 5 2 2, 3 7 2 3, 5 11 4 2, 6, 7, 8 13 4 2, 6, 7, 11 17 8 3, 5, 6, 7, 10, 11, 12, 14 19 6 2, 3, 10, 13, 14, 15 23 10 5, 7, 10, 11, 14, 15, 17, 19, 20, 21 29 12 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27 Primitivwurzeln modulo Primzahlpotenzen
Ist p eine ungerade Primzahl dann ist eine Primitivwurzel modulo
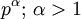 auch Primitivwurzel modulo kleineren Potenzen von p. Interessant für die Suche nach Primtivwurzeln modulo höheren Potenzen von p ist, dass eine Primitivwurzel γ modulo p2 (mit
auch Primitivwurzel modulo kleineren Potenzen von p. Interessant für die Suche nach Primtivwurzeln modulo höheren Potenzen von p ist, dass eine Primitivwurzel γ modulo p2 (mit 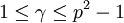 ) auch Primitivwurzel zu allen höheren Potenzen von p ist.[1]. Daher genügt es für höhere Potenzen der Primzahl,
) auch Primitivwurzel zu allen höheren Potenzen von p ist.[1]. Daher genügt es für höhere Potenzen der Primzahl,-
- eine Primitivwurzel γ1 modulo p zu finden (unter den Zahlen
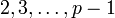 ),
),
- eine Primitivwurzel γ1 modulo p zu finden (unter den Zahlen
-
- die Zahlen
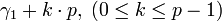 daraufhin zu testen, ob sie Primtivwurzeln modulo p2 sind - notwendig und bereits hinreichend dafür ist, dass
daraufhin zu testen, ob sie Primtivwurzeln modulo p2 sind - notwendig und bereits hinreichend dafür ist, dass 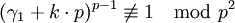 ist. Tatsächlich tritt dies bereits für k = 0 oder k = 1 ein, d. h. γ1 oder γ1 + p ist eine Primitivwurzel modulo p2.[1]
ist. Tatsächlich tritt dies bereits für k = 0 oder k = 1 ein, d. h. γ1 oder γ1 + p ist eine Primitivwurzel modulo p2.[1]
- die Zahlen
Dann hat man mit jeder im zweiten Schritt bestimmten Zahl γ2 eine Primitivwurzel modulo pα für beliebige
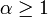 .
.Ist die so bestimmte Primitivwurzel γ2 ungerade, dann ist sie auch Primitivwurzel modulo
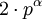 , sonst gilt dies für γ2 + pα.
, sonst gilt dies für γ2 + pα.Anwendungsbeispiel
Primitivwurzeln finden eine Anwendung im Diffie-Hellman-Schlüsselaustausch, einem 1976 veröffentlichten kryptografischen Verfahren zum öffentlichen Schlüsselaustausch. Dessen Sicherheit beruht auf der Tatsache, dass
- es einfach ist, zu einer gegebenen Primzahl m, Primitivwurzel a und ganzen Zahl i ein b auszurechnen mit b = aimod m,
es aber
- aufwendig ist, für ein bekanntes b ein entsprechendes i (den sogenannten diskreten Logarithmus) zu finden.
Literatur
Die Disquisitiones Arithmeticae wurden von Carl Friedrich Gauß auf Lateinisch veröffentlicht. Die zeitgenössische deutsche Übersetzung umfasst alle seine Schriften zur Zahlentheorie:
- Carl Friedrich Gauß: Untersuchungen über höhere Arithmetik (deutsche Übersetzung), Original: Leipzig 1801.
- Peter Bundschuh: Einführung in die Zahlentheorie. 5. Auflage. Springer Verlag, 2002, ISBN 3-540-43579-4, S. 109–120
- Armin Leutbecher: Zahlentheorie - Eine Einführung in die Algebra. 1. Auflage. Springer Verlag, 1996, Berlin Heidelberg New York. ISBN 3-540-58791-8.
Einzelnachweise
Wikimedia Foundation.