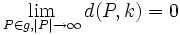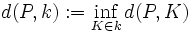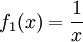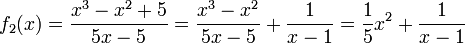- Asymptoten
-
Der Begriff Asymptote (vom Griechischen ἀσύμπτωτος, asýmptōtos, „Nichtübereinstimmende“ vom Verb συμπίπτειν sympiptein „übereinstimmen, zusammenfallen“, von syn, „mit, zusammen“ und píptein, „fallen“[1]) bezeichnet in der Mathematik, vereinfachend ausgedrückt, eine Kurve von einer bestimmten Form, die sich einer vorgegebenen Kurve in einem Grenzprozeß "beliebig annähert“. Die Definition von „Asymptote“ ist uneinheitlich, man unterscheidet im wesentlichen zwei Bedeutungen: Die Asymptoten einer Kurve und die Asymptoten einer Funktion.
Inhaltsverzeichnis
Asymptote einer Kurve
Die hier gegebene Darstellung von Asymptoten ist mehr eine Beschreibung als eine formal saubere Definition.
Kurven im hier betrachteten Sinne sind in einem gewissen Sinne „eindimensionale“ Teilmengen eines euklidischen Raums
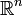 , meist der euklidischen Ebene: Mathematisch sauber definierte Beispiele solcher Kurven sind die Bilder von Wegen, algebraische Kurven und Graphen von stetigen Funktionen mit abzählbar vielen Definitionslücken (dies trifft auf die meisten in der Schule betrachteten Funktionen zu). „Schmiegt“ sich ein Graph an eine Gerade an, so heißt diese Gerade Asymptote.
, meist der euklidischen Ebene: Mathematisch sauber definierte Beispiele solcher Kurven sind die Bilder von Wegen, algebraische Kurven und Graphen von stetigen Funktionen mit abzählbar vielen Definitionslücken (dies trifft auf die meisten in der Schule betrachteten Funktionen zu). „Schmiegt“ sich ein Graph an eine Gerade an, so heißt diese Gerade Asymptote.Eine Asymptote hier--* einer solchen Kurve k ist eine Gerade g, die sich der Kurve „im Unendlichen beliebig annähert“. Präziser bedeutet das, dass der Abstand, den ein Punkt P von g zur Kurve k hat, gegen 0 konvergiert, wenn P entlang der Geraden ins Unendliche wandert. Formal könnte man es so aufschreiben:
Dabei ist der Abstand von P zu k definiert als das Infimum der Abstände von P zu den Punkten von k:
Für eine algebraische Kurve lässt sich der Asymptotenbegriff aus Sicht der projektiven Geometrie auch so beschreiben:
- Eine Asymptote ist eine Tangente im Unendlichen.
Asymptote einer Funktion
Eine Asymptote ist ein Graph (zum Beispiel eine Gerade), der sich dem Graphen einer gegebenen Funktion beliebig weit annähert. Asymptoten von Funktionen betrachtet man insbesondere im Rahmen einer Kurvendiskussion.
Man hat dabei eine Funktion f von D nach
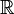 vorgegeben, deren Definitionsbereich D eine Teilmenge von
vorgegeben, deren Definitionsbereich D eine Teilmenge von 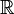 ist.
ist.Man unterscheidet zwischen zwei verschiedenen Typen von Asymptoten, da sich eine Funktion entweder in x- oder in y-Richtung annähern kann.
Annäherung in y-Richtung
Hat f an der Stelle t eine Polstelle, d. h. gilt
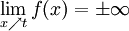 oder
oder 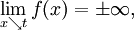
dann nennt man die Gerade x = t eine senkrechte (oder vertikale) Asymptote von f oder eine Polgerade von f.
Annäherung in x-Richtung
Konvergiert f für x gegen
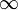 gegen eine reelle Zahl h, d. h. gilt
gegen eine reelle Zahl h, d. h. gilt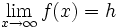 ,
,
dann nennt man die Gerade y = h eine waagerechte (oder horizontale) Asymptote von f. Analoges gilt für den Grenzwert
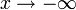 .
.Ist p: R → R eine Gerade, der sich f beim Grenzübergang nach
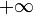 oder
oder 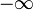 beliebig annähert, d. h. gilt
beliebig annähert, d. h. gilt![\lim_{x\to\infty} [f(x)-p(x)] = 0](/pictures/dewiki/99/c50c36d0408b95576933e5179bab84b1.png) oder
oder ![\lim_{x\to-\infty} [f(x)-p(x)] = 0,](/pictures/dewiki/54/6b610d5ee69178b2bd764a1d09072319.png)
dann nennt man p eine schräge Asymptote von f.
Diese drei Arten von Asymptoten zusammen ergeben genau die Asymptoten des Graphen von f, aufgefasst als Kurve im Sinne des oberen Abschnittes „Asymptote einer Kurve“.
Der Begriff der schrägen Asymptote wird manchmal dahingehend verallgemeinert, statt Geraden bestimmte „einfache“ Funktionen zuzulassen, die die obige Limes-Bedingung erfüllen (Näherungskurven).
So kann man zum Beispiel beliebige Polynome als schräge Asymptoten zulassen. Ist f = g/h eine rationale Funktion (mit Polynomen g und h), dann hat f stets eine schräge Asymptote in diesem Sinne. Sie ist das bei Polynomdivision von g durch h entstehende Polynom p. Der senkrechte Abstand von f zu p wird durch die echt gebrochenrationale Restfunktion angegeben, die dieselben senkrechten Asymptoten wie f hat und zusätzlich die waagerechte Asymptote y = 0.
Man kann aber auch beliebige andere Klassen von Funktionen zu schrägen Asymptoten erklären, sofern sie die Limes-Bedingung erfüllen. Je nach Verwendungszweck ist die eine oder andere Definition angemessener.
Beispiele
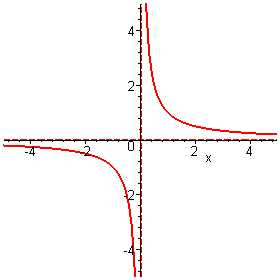
Die Funktion (siehe Hyperbel)
hat die Polstelle, bzw. senkrechte Asymptote bei x = 0 und die waagerechte Asymptote y = 0.
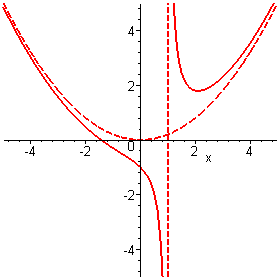
Die Funktion
hat die Polstelle bei x = 1 und (wenn man Polynome als schräge Asymptoten zulässt) die Näherungsparabel
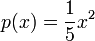 .
.Quellen
- ↑ Duden, das große Fremdwörterbuch, Mannheim & Leipzig, 2000, ISBN 3-411-04162-5
Wikimedia Foundation.